4.5. Дискретно-распределенный фильтр

Схема полузвена дискретно-распределенного фильтра с потерями (рис. 4.12) состоит из индуктивности L_к/2 = L_pl/2, емкости С_к/2 = С_рl/2, равномерно распределенных по длине l/2, сосредоточенных элементов C_b/2 и 2R_b. Такой эквивалентной схемой можно представить входное сопротивление УЭ, параллельно подключенного к катушке индуктивности, расположенной над корпусом (под также можно понимать число витков катушки индуктивности), или к отрезку длинной линии. В первом случае Lp и С_р не связаны между собой, а во втором - связаны известным соотношением

где ε, μ - диэлектрическая и магнитная проницаемость среды; с^* -скорость света.

Таблица 4.1. Определение расчетных параметров ПТФ при заданных

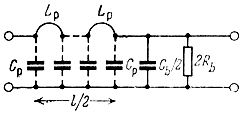
Рис. 4.12. Схема полузве на дискретно-распределенного фильтра с потерями

Вводя обозначения:

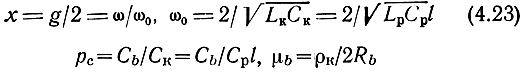
и учитывая (4.3), из (4.4) и (4.5) определим матрицу Α-параметров полузвена ДРФ

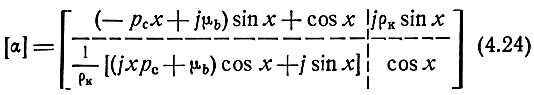
и формулы для характеристических параметров с учетом потерь

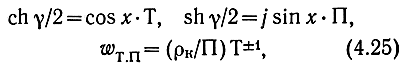
где

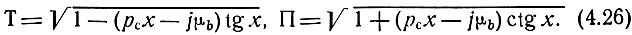
При малых потерях имеем

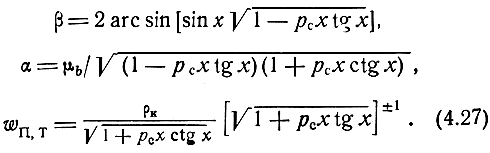
Полоса пропускания ДРФ ограничивается частотой среза, определяемой из трансцендентного уравнения

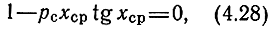
где

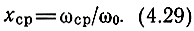
Зависимость x_cp = f(p_c) построена на рис. 4.13. С изменением р_с от 0 до ∞ х_ср уменьшается от π/2 до 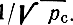. Путем разложения tgx_cp при малых x_ср и при х_ср, близких к π/2, в ограниченный степенной ряд можно найти приближенные формулы, пригодные для инженерного расчета при p_с > 1

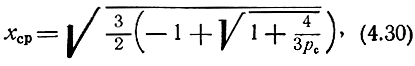
при p_с < 1

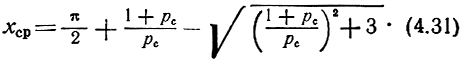
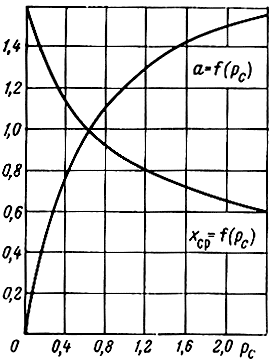
Рис. 4.13. К расчету параметров дискретно-распределенного фильтра

Как правило, р_с > 1 и, следовательно, чаще используемым является соотношение (4.30).

Ход частотных зависимостей характеристических сопротивлений и фазовой постоянной ДРФ без потерь имеет вид, аналогичный виду соответствующих частотных зависимостей ФНЧ k. На низких частотах характеристические сопротивления равны

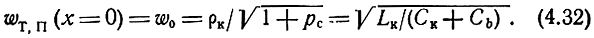
Согласно (4.32), w_Т,П (х = 0) есть низкочастотное значение характеристических сопротивлений ФНЧ k, полученного из ДРФ путем отнесения общей распределенной емкости к сосредоточенной емкости С_b.

Произведение

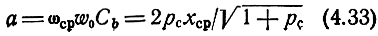
с помощью x_cp = f(p_c) (рис. 4.13) или формулы (4.29) может быть выражено как функция р_c. Зависимость a = f(P_c) (рис. 4.13) необходима для расчета элементов фильтра. Величина параметра а не может превышать значение, равное двум, т. е. задание а > 2 нереально. Это связано с тем, что при р_с → ∞ (С_k → 0) схема ДРФ вырождается в схему ФНЧ типа k, для которого а = 2. Приведенные соотношения позволяют наметить порядок расчета параметров ДРФ для двух случаев: при использовании распределенной катушки индуктивности и отрезка длинной линии. Порядок расчета и расчетные формулы приведены в табл. 4.2.

Таблица 4.2