4.4. Полосовой трехэлементный фильтр

Схема полузвена полосового трехэлементного фильтра с учетом сопротивлений потерь показана на рис. 4.10. Введем обозначения, аналогичные обозначениям в (4.7):

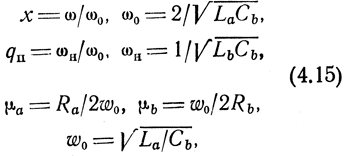
где х - относительная частота; ω₀ и w₀ - соответственно частота среза и низкочастотное волновое сопротивление ФНЧ k без потерь, получаемого из ПТФ при отсутствии L_b; q^υ_П - параметр, характеризующий полосовые свойства фильтра; ω_н нижняя частота среза фильтра без потерь, равная резонансной частоте параллельной ветви фильтра; μ_а и μ_b - параметры потерь.

Используя (4.2), (4.3) и (4.15), нетрудно найти матрицу Α-параметров полузвена

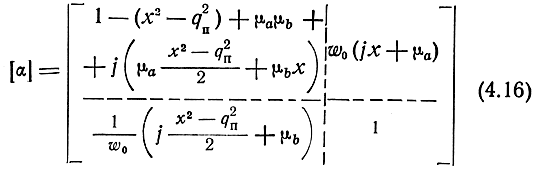
и характеристические параметры

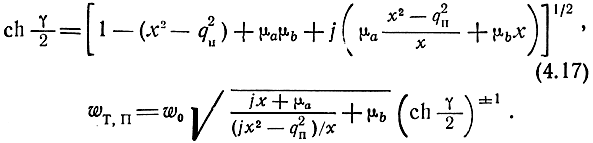
Из (4.16), (4.17) как частный случай при q_п = 0 (т. е. L_b = ∞, ω_н = 0) вытекают матрица (4.6) и формулы характеристических параметров ФНЧ типа k (4.8). Поэтому программа расчета на ЭЦВМ характеристик УРУ, построенных на ФНЧ k или ПТФ, может строиться на базе соотношений (4.16), (4.17).

Полагая малое влияние потерь на характеристические сопротивления и фазовую постоянную, находим приближенные соотношения аналогично тому, как это сделано для ФНЧ k,

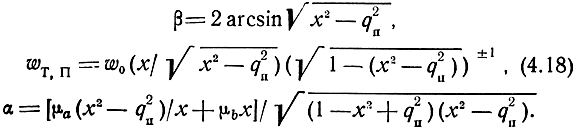
Верхнюю и нижнюю частоты среза можно определить из равенства соответственно β(ω_{ср в}) = π, β(ω_{ср н}) = 0, откуда следуют выражения для относительных частот среза

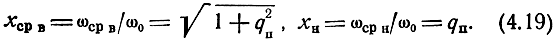
Коэффициент перекрытий частотного диапазона равен

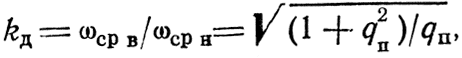
а q_П связан с k_д соотношением

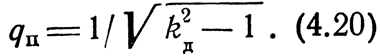
Зависимости от х фазовой постоянной и характеристических сопротивлений полузвена без потерь при k_д = 3 показаны на рис. 4.11.

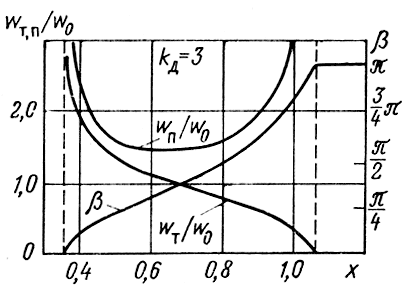
Рис. 4.11. Зависимости характеристических параметров реактивного полосового трехэлементного фильтра от относительной частоты

Волновое сопротивление w_Т изменяется в полосе пропускания от ∞ до 0, a w_Π - от ∞ до ∞, принимая на частоте

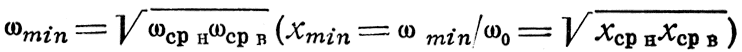
минимальное значение, равное

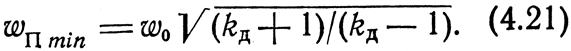
Из формул (4.15), (4.20), (4.21) следует несколько вариантов расчета элементов фильтра в зависимости от совокупности заданных величин. Соответствующие расчетные формулы сведены в табл. 4.1.