5.2. Рабочий коэффициент усиления и условие устойчивости каскада

Проведем анализ рабочего коэффициента усиления K^(z)_E41p для выявления допустимой величины модуля возвратного отношения секции с точки зрения устойчивости каскада УРУ. Близким к реальным условиям является случай, когда η_1,2 = 0 и линии взаимно сфазированы (γ₁ = γ₂ = γ) o При этом необходимо воспользоваться формулой (5.20), применяя к ней соотношения (5.12) и (5.26).

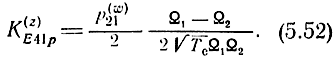
Функции Ω_1,2 (5.26) представляют собой полиномы n-й степени относительно √Т_с вида

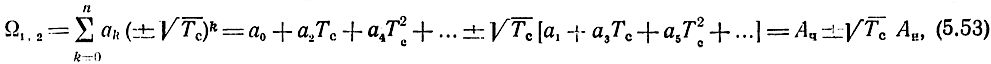
где a_k - комплексные коэффициенты полинома, зависящие от n и γ; А_ч и А_н - полиномы, содержащие a_k соответственно с четными и нечетными индексами. Подставляя (5.53) в (5.52), находим

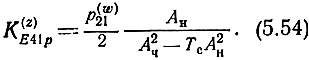
Из (5.54) видно, что коэффициент усиления становится равным бесконечности (что говорит о самовозбуждении) при

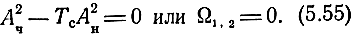
Решение (5.55) относительно Т_с в общем зиде для n > 3 практически невозможно. Поэтому рассмотрим некоторые частные случаи.

Для n = 1, 2 и 3

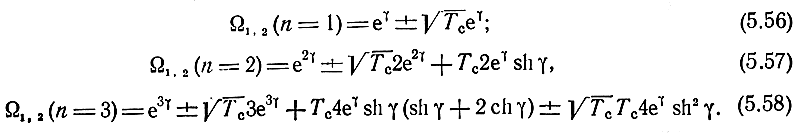
Для любого n a₀ = e^nγ, a₁ = e^nγ. Другие коэффициенты выражаются через n и γ более сложным образом. Однако можно показать, что при γ → 0, jπ, a_k (k≥ 2) стремятся к нулю. Действительно, из (5.12) и (5.26) следует, что при

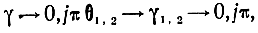
а

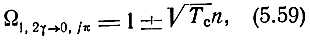
Корни уравнения (5.55) в доступных для решения случаях имеют вид

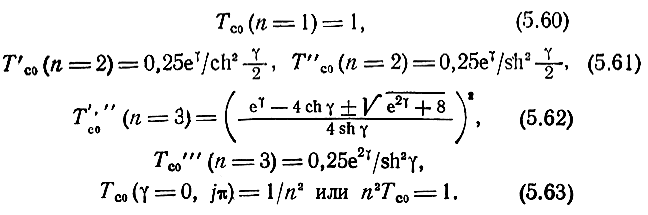
Условие (5.63) физически вполне понятно, поскольку T_c0n² есть возвратное отношение каскада, в котором, в силу принятых значений фазовых постоянных γ = jβ = 0, jπ, УЭ можно считать включенными между собой параллельно, последовательно, последовательно-параллельно или параллельно-последовательно, т. е. в соответствии со структурой каскада.

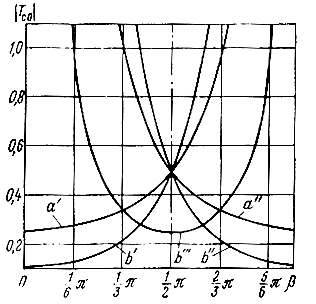
Рис. 5.1. зависимости |T_c0| = f(β): |T_c0^I,II,III| = a^I,II для n = 2, |T_c0^I,II,III|b^I,II,III для n = 3

Допустим, что потери в передающих линиях отсутствуют (γ = jβ, α = 0). Рассмотрим зависимости модуля |T_с0| от β для n = 2 и 3 (рис. 5.1). Как видно из приведенных зависимостей, модули возвратного отношения секции, являющегося - корнем уравнения (5.55) равны или больше 1/n^2*

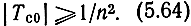
^* ( Для n = 4 и 5 расчет на ЭЦВМ позволяет сделать аналогичный вывод)

Поэтому для выполнения условий устойчивости каскада во всем диапазоне изменения β достаточно, чтобы

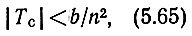
где b - коэффициент, меньший единицы, величина которого выбирается из соображений запаса устойчивости каскада (b = 0,5÷0,8).

При наличии в ПЛ значительных потерь уравнение Ω_1,2 = 0 (5.26) можно записать в виде

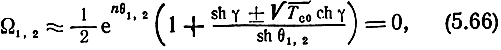
откуда следует

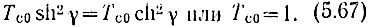
Равенство (5.67) говорит о том, что при значительных потерях в ПЛ условие самовозбуждения каскада совпадает с условием самовозбуждения отдельно взятой секции (5.60). Поэтому при увеличении потерь условие устойчивости каскада более легко выполняется. Секции оказываются как бы развязанными относительно друг друга, и самовозбуждение возможно при выполнении условия (5.67) внутри каждой секции. Это говорит о том, что если каскад устойчив при отсутствии потерь, то при наличии потерь он будет более устойчив.

Таким образом, при полном согласовании каскада и отсутствии взаимной расстройки ПЛ для обеспечения устойчивой работы каскада УРУ необходимо выполнить условие (5.65), из которого следует, что возвратное отношение секции должно быть достаточно малым.