5.4. Коэффициент передачи от источника в k-м усилительном элементе

Допустим, что в какой-либо ветви эквивалентной схемы k-го усилительного элемента однородного каскада УРУ (рис. 5.2) содержится независимый источник напряжения E^(k) или тока J^(k) для обозначения которых используем символ И^(k). При этом предполагаем отсутствие в каскаде других независимых источников. Необходимо определить коэффициент передачи

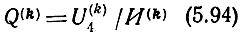
как отношение комплексной амплитуды напряжения на сопротивлении нагрузки Z₄ к комплексной амплитуде напряжения или тока в k-м УЭ. Коэффициент передачи Q^(k) в дальнейшем потребуется для определения активной мощности, развиваемой на сопротивлении нагрузки от действия в к-м УЭ некоторого источника шума. Q^(k) необходимо представить в виде функции параметров фильтров и УЭ, нагрузочных сопротивлений, числа секций и номера рассматриваемой секции k. Для этого воспользуемся полученными в § 2.4 соотношениями, приближенными матрицами Α-параметров каскада (3.41), (3.42) и левой части каскада, содержащей (k-1) секцию и левую полусекцию (3.48), (3.49), а также теорией автономного четырехполюсника [29].

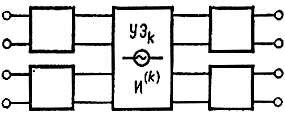
Рис. 5.2. k-я секция каскада с автономным УЭ

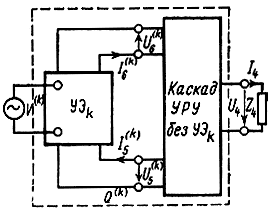
Рис. 5.3. Четырехполюсник, образованный из каскада путем выделения в k-м УЭ ветви с независимым источником сигнала

УЭ с номером к представляет собой автономный четырехполюсник. Если из него вынести за пределы каска-да ветвь, содержащую независимый источник,- то цепь, по которой сигнал передается к нагрузочному сопротивлению, может быть представлена в виде линейного не автономного четырехполюсника, имеющего коэффициент передачи Q^(k) (рис. 5.3). Согласно теории автономного четырехполюсника действие независимого источника в k-м УЭ эквивалентно действию его автономных параметров, представляющих собой вынесенные на полюса источники тока и напряжения (рис. 5.4), которые находятся:

для УЭ структуры у (рис. 5.4,а) как токи в полюсах при их коротком замыкании

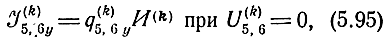
для УЭ структуры z (рис. 5.4,6) как напряжения на полюсах при их размыкании

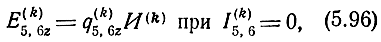
для УЭ структуры z (рис. 5.4,в) как напряжение и ток соответственно на входных полюсах при холостом ходе и в выходных полюсах при коротком замыкании

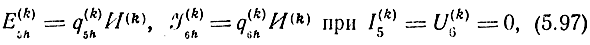
для УЭ структуры g (рис. 5.4,г) как ток и напряжение соответственно на входных полюсах при коротком замыкании и на выходных полюсах при холостом ходе

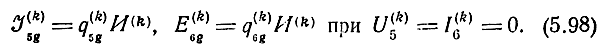
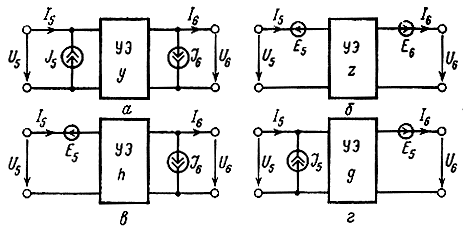
Рис. 5.4. УЭ с эквивалентными автономными источниками

Формулы для определения напряжения U₄ от действия источников на полюсах УЭ найдены в § 2.4. Поэтому, полагая, что для каждой структуры имеется только два автономных параметра, и подставляя (5.95) - (5.98) (в (2.59), определим:

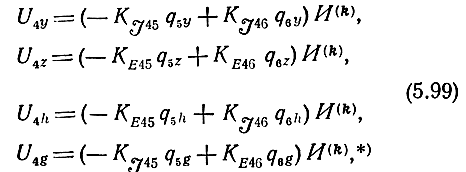
^* (В (5.99) и далее индекс k опущен для упрощения записи)

где K_E,J⁴⁵ и K_E,J⁴⁶ находятся по формулам (2.60), в которые необходимо подставить нормированные относительно характеристических сопротивлений фильтров элементы приближенных (при малой обратной связи) нормированных Л-матриц каскада (3.41), (3.42) и левой его части, состоящей из (k-1) секции и левой полусекции (3.48), (3.49).

При использовании нормированных Α-параметров необходимо считать нормированными: U₄ относительно w_H2 E₅(J₅) относительно w_B1, Е₀(J₆) относительно w_В2. Поэтому при ненормированном И коэффициенты q в (5.99) приобретают нормировку:

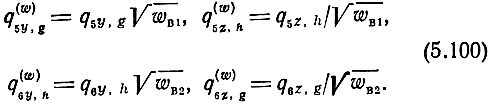
Таким образом, в (5.99) все величины, кроме И, будем полагать нормированными относительно характеристических сопротивлений и обозначать индексом (w).

В (2.60) Α-параметры определены в СК χ. Если для каждой структуры K^(w)_45,46 выразить через элементы матриц в СК соответственно π, ξ, μ, ε то можно убедиться, что (2.60) объединяются в следующие два соотношения:

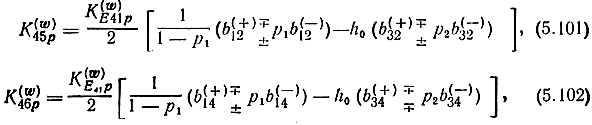
поскольку матрицы нормированных относительно характеристических сопротивлений Л-параметров для различных структур в собственных системах координат формально одинаковы. В (5.101), (5.102):

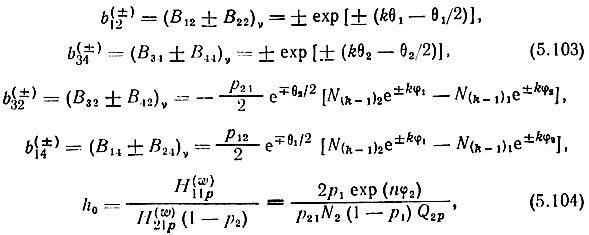
последовательность знаков перед pi соответствует последовательности структур y, z, h, g.

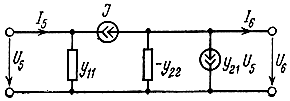
Рис. 5.5. Пример автономной схемы УЭ при отсутствии обратной связи

Подстановка (5.101), (5.102) в (5.99) с учетом обо-значений (5.103), (5.104) окончательно формирует выражение для нормированного коэффициента передачи Q^(w) определенного как отношение нормированной амплитуды напряжения

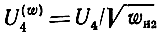
к ненормированной амплитуде источника И^(k):

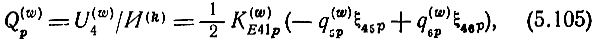
где

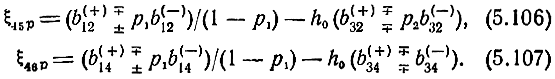
При отсутствии обратной связи через УЭ (p_1,2 = 0) b⁽⁺⁾₁₄ = 0. Кроме того, θ_1,2 = γ_1,2 и выражение (5.105) становится точным. Следует обратить внимание на тот факт, что отсутствие обратной связи в общем случае не означает q₅ = 0. Например, для схемы УЭ, показанной на рис. 5.5, y₁₂ = 0, но q_5,6 = 1.

Практический интерес представляет случай, когда обратная связь и рассогласование с нагрузочными сопротивлениями малы. При этом

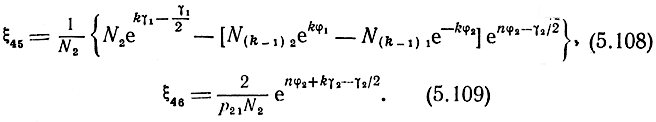
Формулу (5.108) можно представить в другом более наглядном (виде

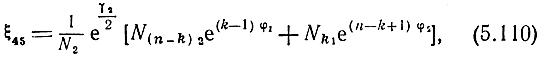
где

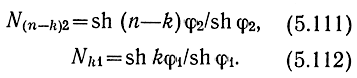
В (5.110) первое слагаемое характеризует передачу от Е₅ или J₅ в k-и секции через (n - k) правых секций на выход каскада, а второе - передачу через k левых секций также на выход каскада. Коэффициент усиления K_E41p при p₁₂ = 0 и p_i = 0 определяется выражением (5.92).