5.6. Оценка максимально допустимого рассогласования передающих линий

Оценку максимально допустимого рассогласования можно провести по максимально допустимым значениям КСВН на входе и выходе или по колебательной неравномерности АЧХ каскада. Возьмем случай отсутствия взаимной расстройки (γ₁ = γ₂ = γ) и потерь (γ = jβ) ПЛ, поскольку при этом наблюдается наибольшая волнообразность характеристик. Для простоты пренебрегаем обратной связью в каскаде и полагаем η₁ = η₂ = η₃. В данном случае необходимо воспользоваться формулами (5.37), (5.39). Требуется определить максимально допустимое отклонение от единицы отношения нагрузочного сопротивления и наружного характеристического сопротивления фильтров ПЛ

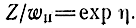
Положим, что Z = R а w_H - активная величина равная

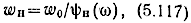
где w₀ - характеристическое сопротивление фильтра на квазирезонансной частоте; ψ_H(ω)-функция частотной зависимости w_H (например, для ФНЧ типа k, если wn~wn , то

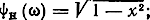
если w_H = w_T, то

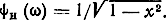
Тогда

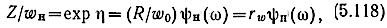
а максимальное отклонение будет определяться как отношением r_w = R/w₀, так и функцией ψ_H(w).

Из формулы (1.5) следует, что при максимально допустимом КСВН, равном двум, величина модуля внешнего коэффициента отражения не должна превышать ¹/₃:

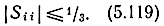
Формула для |S_ii| может быть получена из (5.39)

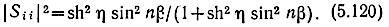
В (5.120) sh η есть медленная функция частоты. Поэтому распределение экстремумов зависимости |S_ii(ω)| в диапазоне частот в основном определяется зависимостью sin β от частоты:

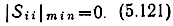
при sin nβ = 0,

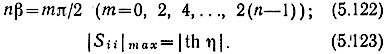
при sin nβ = ±1,

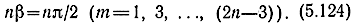
На краю полосы пропускания (β = π) m = 2n, η = ±∞ и |S_ii| = 1. Число экстремумов равно 2n, если считать точку β = π. Расположение экстремумов наглядно иллюстрируется зависимостями КСВН для n = 3, 4 (рис. 4.14, 4.15), рассчитанными на ЭЦВМ. Если по (5.121) - (5.124) найти значения х, соответствующие экстремумам, то для n = 4 получим x_min = 0; 0,38; 0,707; 0,92; х_max = 0,19; 0,55; 0,83, что достаточно хорошо совпадает с величинами, определяемыми непосредственно из рис. 4.16.

При условии t(5.119) из равенства (5.123) найдем

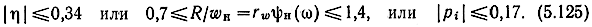
Неравенство (5.125) позволяет для каждого конкретного выражения функции ψ_H(ω) рассчитать оптимальное значение величины r_w. Из (5.125) следует практический вывод о том, что при заданных нагрузочных сопротивлениях для согласования в возможно большей полосе частот передающие линии необходимо выполнять с w₀, приблизительно на 20-30% большим или меньшим нагрузочных сопротивлений в зависимости от того, какие полузвенья фильтров стоят на концах каскада. Если линия оканчивается Т-образной стороной полузвена фильтра, то w₀ необходимо брать больше R_i, если П-образной стороной, то w₀ < R_i. Данный вывод подтверждается соответствующими расчетными зависимостями рис. 4.14, 4.16.

Во многих случаях ψ_П(ω) можно представить выражениями

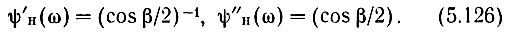
Тогда появляется возможность определить величины максимумов:

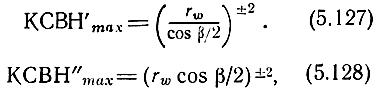
при β/2 = mπ/4n, m = 1, 3, 5, ..., 2n-3, по которым можно судить об оптимальной величине r_w. Так, например, при равенстве величин первого и последнего максимумов КСВН для n = 3 r_wopt = 0,83 (или 1,2), КСВН_max = 1,36; для n = 4 r_wopt = 0,73 (или 1,36), КСВН_max = 1,76. Коэффициент усиления при сделанных допущениях равен

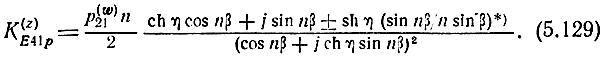
^* (Перед sh η знак плюс для структур y, h, знак минус для структур z, g. )

Зависимости модуля КЕЫР от частоты для n = 3; 4, рассчитанные на ЭЦВМ по методике, изложенной в гл. 4, показаны на рис. 4.15, 4.17. Сравнивая рис. 4.14, 4.16 с рис. 4.15, 4.17, видим, что экстремумы |K_E41p| достаточно хорошо совпадают с экстремумами КСВН, и для определения их места расположения на оси частот можно пользоваться условиями (5.122), (5.124):

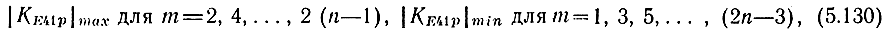
для m = 0 может быть минимум при η < 0 или максимум при η > 0.

Отношение

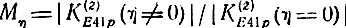
характеризует быструю неравномерность АЧХ каскада

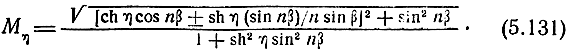
С учетом (5.122), (5.124), (5.130) из формулы (5.131), определим: M_{η max} = ch η при m четных (m ≠ 0),

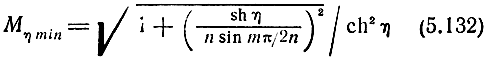
при m нечетных,

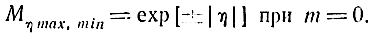
Потребуем, чтобы выполнялось условие

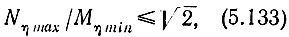
которое накладывает определенные ограничения на величину η. Имея в виду, что М_{η min} > l/ch²η, оценим допустимое значение η для двух случаев: а) когда участок диапазона частот при малых β может не рассматриваться (такая ситуация возникает в УРУ нижних частот при использовании цепей низкочастотной коррекции, определяющих форму АЧХ в этом диапазоне); б) когда важен весь диапазон частот (например, в УРУ, построенных на полосовых фильтрах).

В первом случае

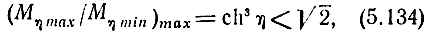
во втором случае

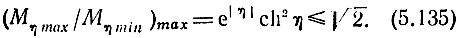
Из (5.134) имеем

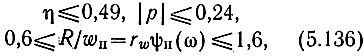
что является более легким условием по сравнению с (5.125). Поэтому в данном случае необходимо учитывать требование, определенное, исходя из КСВН. Во втором случае

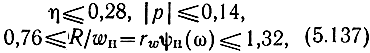
и, очевидно, условие (5.137) становится основным.

Таким образом, чтобы в реальной полосе частот (например, при x < 0,85-0,9) КСВН не превышал двух, а полный размах быстрой неравномерности АЧХ был менее ЗдБ, необходимо выполнить следующие условия: в случае а) (5.125), б) (5.137).