5.7. Влияние потерь и взаимной расстройки передающих линий на АЧХ каскада

Для анализа влияния потерь и взаимной расстройки на АЧХ каскада допустим, что обеспечено достаточно хорошее согласование ПЛ (p_i << 1). Кроме того, положим, что обратная связь пренебрежимо мала.

Формула для ненормированного коэффициента усиления, в которой одновременно учитываются потери и взаимная расстройка, может быть получена из (5.50):

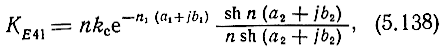
где

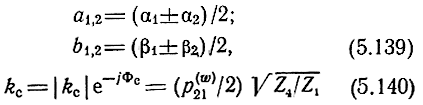
- коэффициент усиления одной секции без потерь и расфазировки.

Модуль и фаза рабочего коэффициента усиления равны

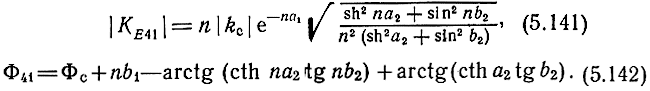
В практике построения схем УРУ наиболее часто встречаются три случая:

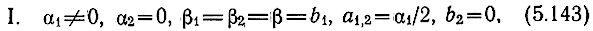
потери имеются только во входной ПЛ; для уменьшения спада АЧХ в диапазоне частот в результате увеличения потерь стремятся уравнять фазовые постоянные;

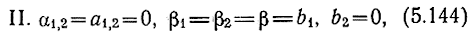
в некотором смысле идеальный случай, когда потери и расфазировку можно считать пренебрежимо малыми;

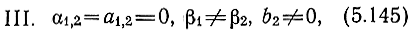
имеется взаимная расстройка ПЛ, которая может использоваться для устранения подъема АЧХ каскада, наблюдающегося при отсутствии потерь.

Обозначая модули рабочих коэффициентов усиления в указанных случаях соответственно |K_41,I,II,II| и принимая во внимание условия (5.143-5.145), запишем:

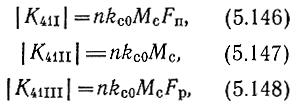
где k_c0 - модуль коэффициента усиления одной секции (5.140) на квазирезонансной частоте (например, для ФНЧ типа k на низких частотах),

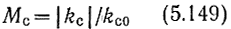
- относительная АЧХ одной секции,

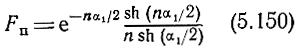
- функция потерь, отражающая изменение коэффициента усиления при изменении потерь во входной ПЛ,

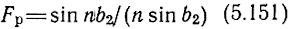
- функция расфазировки, характеризующая изменение коэффициента усиления при увеличении взаимного отличия фазовых постоянных ПЛ. Отметим также, что частотная зависимость Мс обусловлена зависимостью от частоты ненормированного параметра прямой передачи УЭ и зависимостью от частоты характеристических сопротивлений. Если обозначить

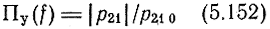
- относительную частотную зависимость параметра прямой передачи УЭ (p_{21 0}) = |p₂₁| на квазирезонансной частоте), а V_w(f)-относительную частотную зависимость функции характеристических сопротивлений в (5.140), то

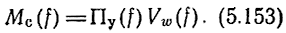
На квазирезонансной частоте M_c = П_У = V_w= 1. При α₁ или b₂, равных нулю F_п.р = 1. С увеличением α₁ или b₂ F_п.р уменьшаются. В случае, если M_c(f) = const или падает с изменением частоты, необходимо принять меры к уменьшению щ или Ь%. Очевидно, что при этом потери и расфазировка оказывают отрицательное влияние на АЧХ каскада. Поэтому необходимо ограничить их величину значениями, до которых F_п.р практически можно считать равными единице. В случае, если M_c(f) имеет тенденцию роста в диапазоне частот, то для выравнивания АЧХ каскада целесообразен некоторый оптимальный спад F_п.р. При этом потери и расфазировка выполняют роль полезных корректирующих факторов.

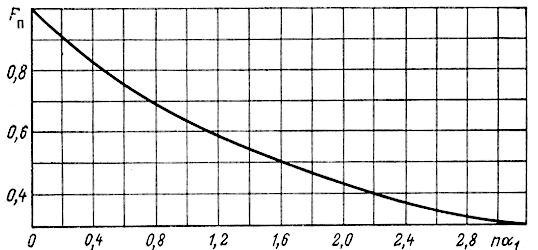
Рис. 5.6. Функция потерь

Не затрагивая в настоящем параграфе вопросов коррекции АЧХ, рассмотрим поведение и свойства функций потерь и расфазировки, а также определим допустимые значения α₁ для случая M_c(f) ≤ 1. Функция потерь (5.150) с точностью не хуже 10% при n ≥ 2, u₁ ≤ 1,6 может быть представлена формулой

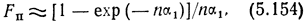
откуда следует, что при указанных условиях F_п зависит только от произведения nα₁ т. е. F_п = const, если при изменении n и α₁ = const. Это свойство оказывается весьма полезным при оптимизации параметров каскада, если число секций варьируется. Зависимость F_п = f(nα₁), рассчитанная по (5.154), показана на рис. 5.6.

В ряде случаев для F_п требуется выражение, не содержащее трансцендентных функций, но отражающее основные свойства (5.150), (5.154). Достаточно хорошая аппроксимация достигается функцией

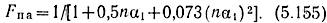
Коэффициенты в (5.155) выбраны, исходя из требований: F_па = F_п = 1 При nα₁ = 0; F_па = F_п = 0,3 при nα₁ = 3,2; F_па'(0) = F_п'(0) = - 0,5. В середине интервала nα₁ = 0 - 3,2 погрешность (5.155) относительно (5.154) не превышает 5%, а относительно (5.155) -10%. Кроме того, существенно, что F_па, так же как F_п, при nα₁, стремится к нулю. Из (5.155) можно определить паи соответствующее некоторому уровню F_п,

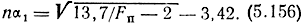
Для этого же можно использовать графическую зависимость на рис. 5.6. для определения допустимого значения α₁ потребуем, чтобы F_п ≥ F_{п доп} где F_{п доп} достаточно близкая к единице величина, например, F_{п доп} = 0,9. Тогда, разлагая числитель в (5.154) в ограниченный степенной ряд, найдем

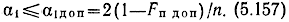
Поскольку собственное затухание фильтров возрастает с приближением частоты к частоте среза, то α₁ необходимо брать на границе полосы пропускания, которая, как правило, составляет 85-90% частоты среза, т. е. α_1доп(f = 0,85-0,9f_cp). При α₁ ≤ α_{п доп} потери можно считать пренебрежимо малыми.

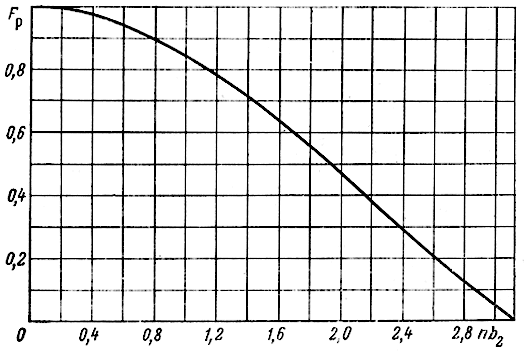
Рис. 5.7. Функция расфазировки

Функция расфазировки, так же как функция потерь, при некоторых реальных ограничениях обладает постоянством nb₂ при F_p = const. При отсутствии потерь число секций, как правило, должно быть более четырех. Кроме того, b₂ ≤ π/n, поскольку иначе АЧХ будет иметь провал в середине полосы пропускания. Поэтому (5.151) можно представить приближенным выражением (рис. 5.7).

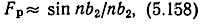
из которого непосредственно следует указанное свойство. Если представить (5.158) в виде бесконечного произведения [39]

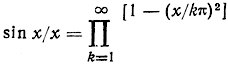
и ограничиться квадратичными членами двух первых сомножителей, то для nb₂ ≤ 2,5 (5.158) аппроксимируется более простым выражением

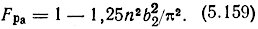
С точностью не хуже 5% в интервале 0 ≤ nb₂ ≤ π (5.158) описывается другой формулой

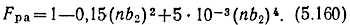
Зависимости (5.159), (5.160) могут быть использованы для расчета и оптимизации АЧХ каскада.

Ограничивая спад Fр значением 0,9, можем оценить допустимую расфазировку передающих линий. Разлагая числитель (5.158) в степенной ряд и ограничивая его составляющими первого и второго порядка малости, получим

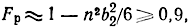
откуда следует, что

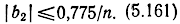
При выполнении неравенства (5.161) расфазировка передающих линий будет вызывать уменьшение коэффициента усиления не более, чем на 10%. Поскольку β_1,2 зависят от частоты, то необходимо требовать выполнения неравенства (5.161) на граничной частоте полосы пропускания. Собственно, настройка каскада УРУ и состоит в обеспечении идентичности фазовых постоянных путем варьирования емкостей или индуктивностей фильтров передающих линий при постоянном контроле за коэффициентами стоячей волны и полосами пропускания линий. Поэтому, как правило, неравенство (5.161) обеспечивается практически.

Неточность изготовления фильтров по расчетным значениям индуктивностей и емкостей вызывает взаимное смещение частот среза фильтров входной и выходной линий и, следовательно, расфазировку. Интересно оценить, каково же допустимое взаимное смещение частот среза, определенное по (5.161). Например, при использовании ФНЧ типа k, для которых фазовая постоянная определяется формулой (4.9), неравенство (5:161) принимает вид

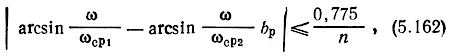
где

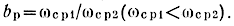
На частоте, равной 0,9ω_c.p1

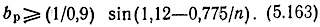
Расчет по (5.163) дает следующие результаты:

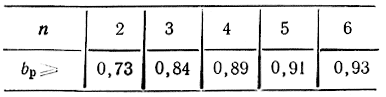
но которым нетрудно судить, используя (4.10), о допустимом взаимном отличии элементов фильтров входной и выходной линии.