6.3.1. Составляющие коэффициента шума наружных источников.

Подставляя (5.91), (5.92) в (6.15), получим

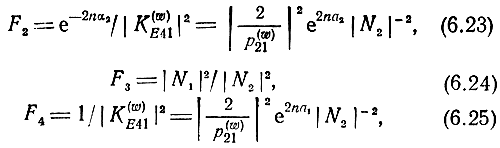
где

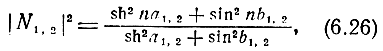
a_1,2 и b_1,2 определяются по (5.139).

Если в выражениях для F_2,4 перейти к ненормированному рабочему коэффициенту усиления^*

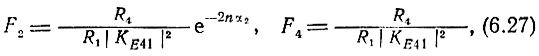
^* ( При полном согласовании каскада нормирование относительно w_H1,2 равносильно нормированию относительно R_i)

то становится ясно, что для уменьшения F_2,4 необходимо увеличивать отношение R₁/R₄(в результате увеличения R₁) и коэффициент усиления каскада (в результате увеличения числа секций и усиления одной секции); частотные зависимости F_2,4 определяются в основном АЧХ каскада. Поскольку абсолютное значение коэффициента усиления (по напряжению) каскада обычно равно трем или более трех, а АЧХ выравнивается с помощью различных способов, то величины F_2,4 находятся в пределах 0,1 и коэффициент усиления для практических расчетов по (6.27) можно считать постоянным в диапазоне частот. Данный вывод подчеркивается еще тем обстоятельством, что F_2,4 значительно меньше единицы и составляющих внутренних шумов.

Из составляющих наружных шумов наибольший интерес представляет F₃. Учитывая (5.143) - (5.145), из формулы (6.24) получаем

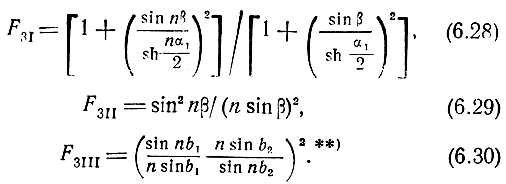
^** (Римские цифры соответствуют номерам условий (5.143) - (5.145).)

Формулы (6.28) - (6.30) могут быть использованы для расчета частотных зависимостей F₃. Для каждого конкретного типа фильтров необходимо использовать соответствующие формулы зависимостей от частоты β_1,2 и α_1,2. Анализ (6.28) - (6.30) показывает, что зависимости F_3I,II(β) четны и при изменении β в пределах от 0 до π симметричны относительно вертикальной оси, проведенной через β = π/2; β = 0, π F₃₁, n = 1; с ростом β от 0 и с уменьшением β от π F_{3I,II (β)} уменьшаются, и тем интенсивнее, чем больше n; в середине интервала 0 < β < π величина F_3I,II измеряется десятыми долями единицы; увеличение затухания приводит к росту составляющей. Зависимости F_3I,II от Р для различных n показаны на рис. 6.3,а, б, в, г. Проведенный анализ позволяет сделать благоприятный вывод о том, что составляющей F_3II в середине некоторого интервала в принципе можно пренебречь. Если ограничить F_3II величиной 0,2, то β₀ для различных n равно:

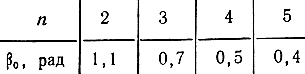
что соответствует при n > 2 достаточно близким к нулю и к единице относительным частотам. Например, при использовании ФНЧ типа k x₀ = ω₀/ω_ср: n = 2 х₀ = 0,52(0,84); n = 3 x₀ = 0,34(0,93); n = 4 x₀ = 0,25 (0,96); n = 5 x₀ = 0,2 (0,97). Поскольку, как правило, конец полосы пропускания (x > 0,9) не реализуется в результате влияния различных факторов, то, как видно из приведенных значений x₀, близких к единице, подъем F_3II до единицы вблизи β = π оказывается вне полосы пропускания. Таким образом, F_3II можно учитывать только при малых β < β₀.

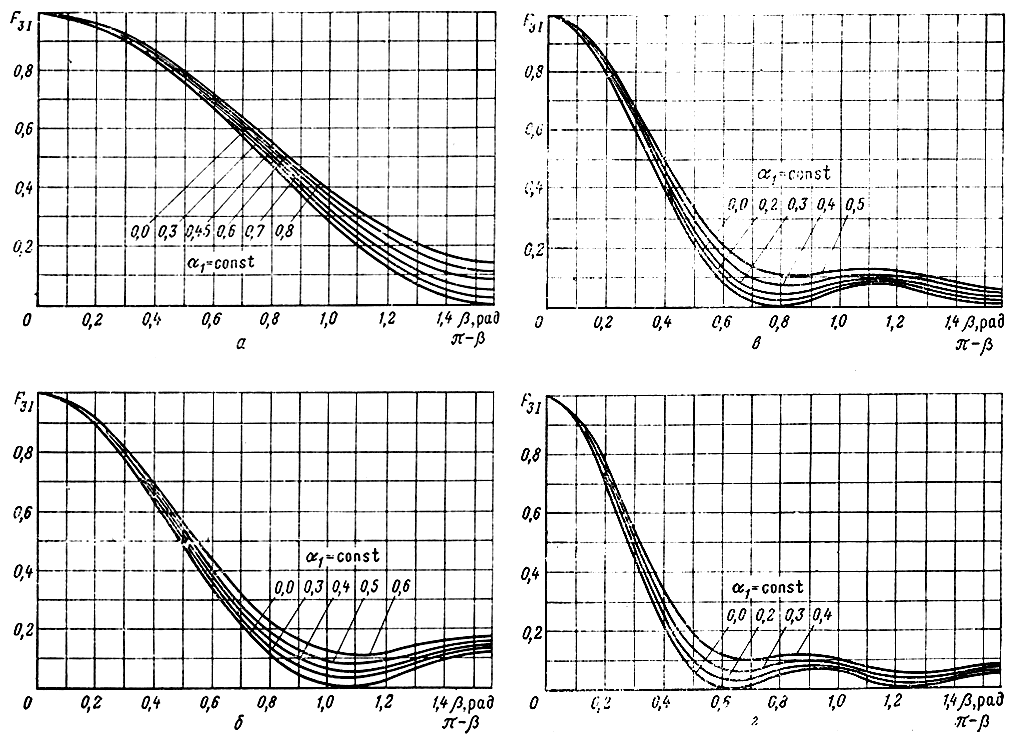
Рис. 6.3. Зависимости составляющей F_3I от фазовой постоянной при различных значениях собственного затухания фильтров входной линии и n: а) n = 2; б) n = 3; в) n = 4; г) n = 5

Для расчета F_3II (6.30) можно использовать F_3II (6.29), поскольку

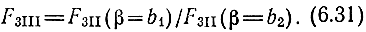
Расфазировка приводит к увеличению F_3II. Поэтому следует избегать искусственно вводимой расфазировки, применяя другие способы выравнивания АЧХ.

Обобщая сказанное, следует отметить, что несмотря на наличие в каскаде УРУ трех наружных источников шума, их влияние на общий F_ш незначительно.