
6.3.2. Составляющие коэффициента шума внутренних источников
Наиболее важной и в то же время наиболее сложной в своей функциональной зависимости от различных параметров каскада является составляющая шумов внутренних источников УЭ.
Рассмотрим случай отсутствия корреляционной связи между источниками шума в к-м УЭ. При этом исходными соотношениями являются (6.19), (6.21) и (5.109), (5.110).
Параметр прямой передачи УЭ p(w)21/2, содержащийся в ξ(k)46, введем в состав q(w)6. Новые величины обозначим:
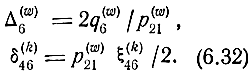
Тогда
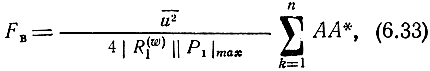
где
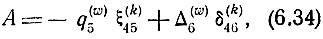
А* - комплексно-сопряженная величина.
Таким образом, параметры УЭ содержатся только в q5 и Δ6, которые от номера к не зависят.
Перемножая AA*, получаем
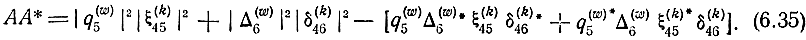
Если обозначить
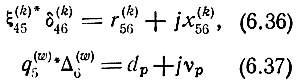
и развернуть в (6.35) последнее слагаемое, то подстановка (6.35) в (6.33) приводит к выражению
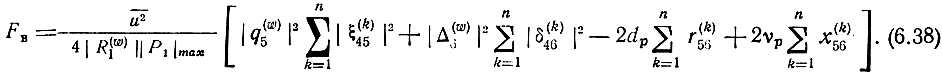
Первое и второе слагаемые (6.38) характеризуют доли FB, обусловленные прохождением шумового сигнала от УЭ на выход каскада соответственно по входной и выходной ПЛ. Последние два слагаемых являются результатом геометрического сложения сигналов, прошедших по входной и выходной ПЛ. Если источник шума сосредоточен на выходных полюсах УЭ, то q5 = 0 и в выражении (6.38) имеется только второе слагаемое. Если источник шума сосредоточен только на входных полюсах УЭ, то q6 = 0 (Δ6 = 0) и выражение (6.38) содержит только первое слагаемое.
В общем случае, когда источники шума находятся в УЭ, все четыре слагаемые присутствуют одновременно.
Исключение составляет случай, когда в результате взаимного сравнения слагаемых некоторыми можно пренебречь.
Вводя обозначения
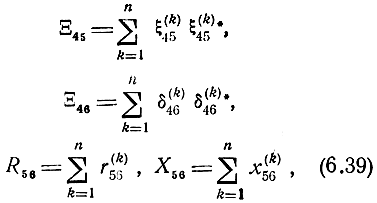
запишем (6.38) в виде
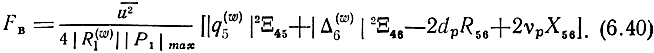
Для случая I (5.143)
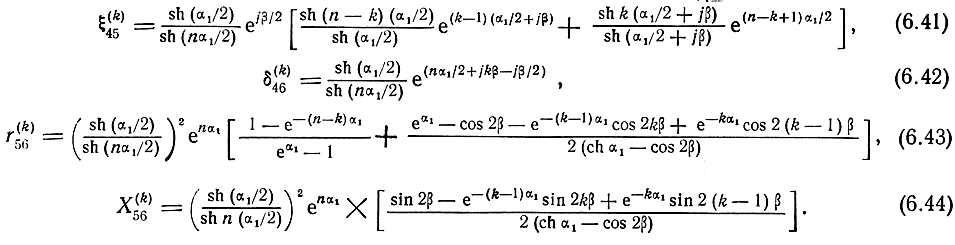
Функцию Ξ46 легко определить для общего случая, без условий (5.143) - (5.145):
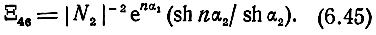
При использовании (6.42) или из (6.45) при b2 = 0, α2 = 0, a1,2 = α1/2 имеем
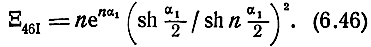
Для случая II при отсутствии потерь во входной линии (α1 = 0)
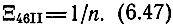
Для случая III (5.145)
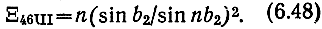
Сравнивая (6.48) с (6.29), видим, что для расчета Ξ46II можно использовать F3II (рис. 6.3, а - г при α1 = 0), заменяя β на b2
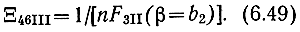
Как видно из (6.47), функция Ξ3II обратно пропорциональна числу секций. Ее можно отождествить с FВ только в том случае, если потери в линиях отсутствуют и источники шума сосредоточены на выходных полюсах УЭ. При наличии потерь обратная пропорциональность нарушается.
Выражение (6.46) можно записать в виде
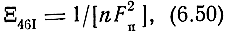
где FП - функция потерь, аппроксимируемая зависимостью (5.155).
Тогда
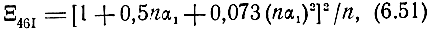
откуда видно, насколько сильно потери во входной линии влияют на величину Ξ46I. Формула (6.51) вполне может использоваться для практических расчетов.
С увеличением расфазировки (b2 ≠ 0) Ξ46 растет (6.45), (6.48), (6.49).
Функция Ξ45 имеет громоздкое выражение. Однако и она может быть приведена к достаточно простому виду. При α1 = 0 свертка суммы приводит к формуле (6.52)
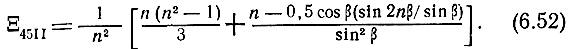
Для наглядности раскроем (6.52) при n = 2, 3, 4
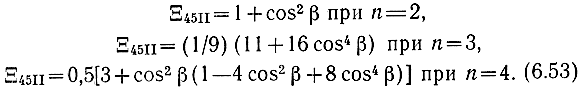
Анализ (6.52), (6.53), а также (6.41) показывает, что Ξ45I,II являются четными функциями относительно β, обладают симметрией относительно вертикальной оси, проведенной через β = π/2, имеют два максимума при β = 0, π и один минимум при β = π/2. Зависимости Ξ45I, рассчитанные на ЭЦВМ для n = 2, 3, 4, 5 и при α1 = const, представлены на рис. 6.4 a - г.
При α1 = 0
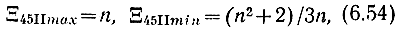
в чем можно убедиться из (6.52), (6.53). Таким образом, перепад в диапазоне частот достаточно большой:
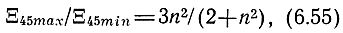
и при n → ∞ стремится к трем. Зависимость (6.52) с точностью не хуже 10% может быть аппроксимирована функцией
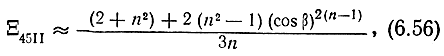
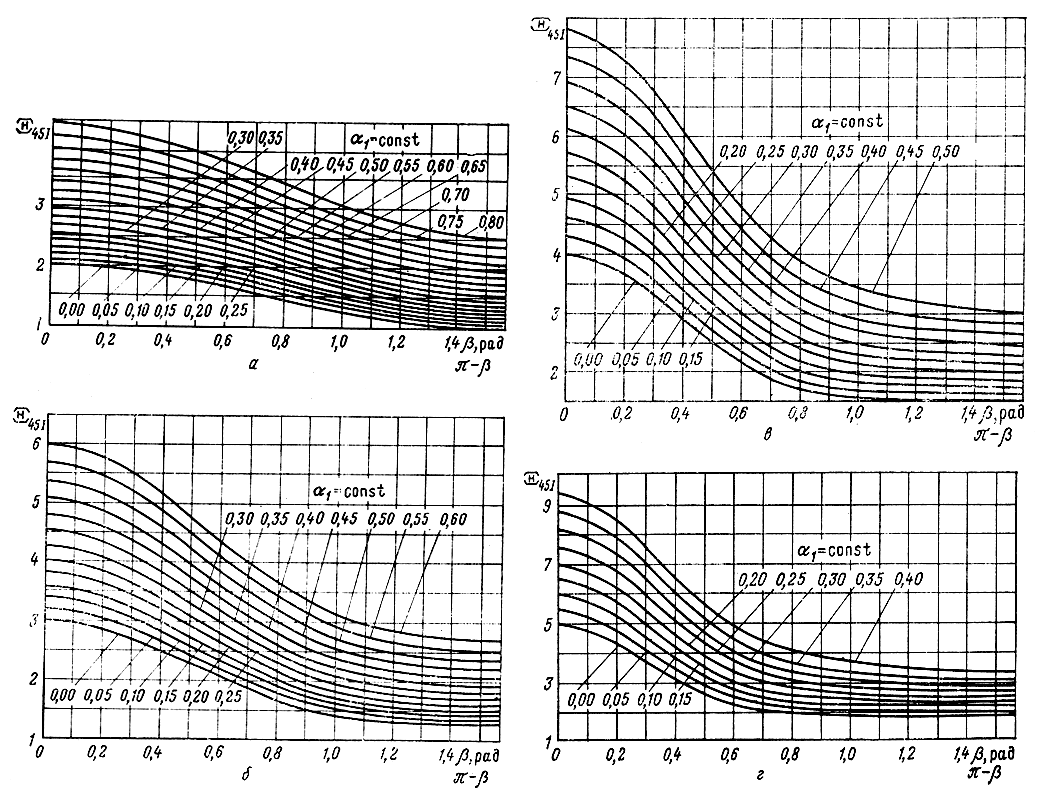
Рис. 6.4. Зависимости функции Ξ45I от фазовой постоянной при различных значениях собственного затухания фильтров входной линии и n: а) n = 2; б) n = 3; в) n = 4; г) n = 5;
Ξ45 = f(n, α, β) может быть представлена приближенным выражением с точностью также не хуже 10%:
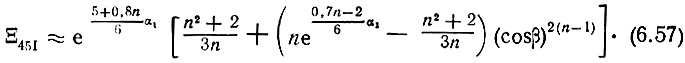
Формулы (6.56), (6.57) могут использоваться для практических расчетов.
Из приведенного анализа следует вывод, что шумы, проникающие из УЭ во входную линию, могут оказаться весьма существенными, поскольку в результате усиления шумов всех УЭ всеми УЭ Ξ45 имеет величину приблизительно в т2 раз большую, чем Ξ46. В этих условиях единственным выходом является применение УЭ с малым значением квадрата модуля параметра q5(w) величина которого должна быть меньше 1/n2. В ряде случаев такое соотношение выполняется.
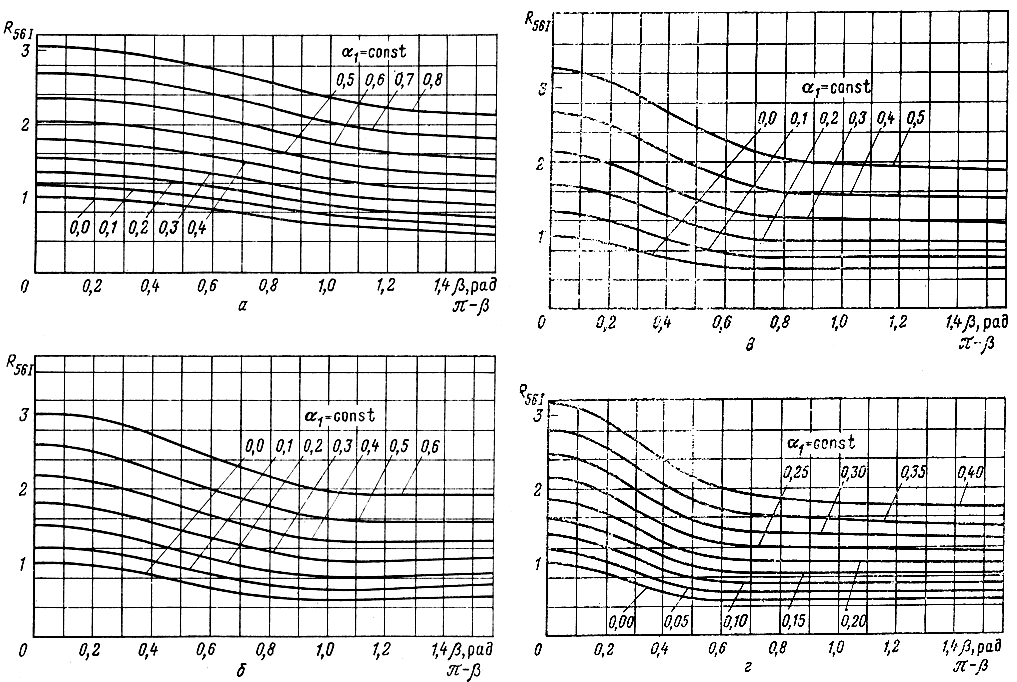
Рис. 6.5. Зависимости функции R56I от фазовой постоянной при различных значениях собственного затухания фильтров входной линии и n: а) n = 2; б) n = 3; в) n = 4; г) n = 5
Как показывает анализ и расчет на ЭЦВМ, функция R56I,II,и симметрична, a X56I,II антисимметрична относительно оси, проведенной через β = π/2, т. е.
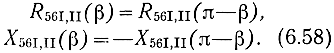
Зависимости R56 и Х56 как функции β и α1 для различных n построены на рис. 6.5, 6.6. Параметр α1 меняется дискретно. При α1 = 0 R45II и X56II равны
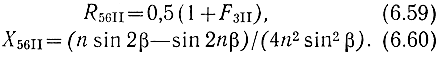
Из всех приведенных расчетных формул и графических зависимостей следует, что потери во входной передающей линии каскада УРУ значительно влияют на величину составляющей коэффициента шума FB. Потери в каскаде УРУ в ряде случаев существенны и их необходимо учитывать.
При отсутствии потерь и при взаимной расстройке ПЛ формулы для Ξ45, R56, X56 (случай III) имеют вид
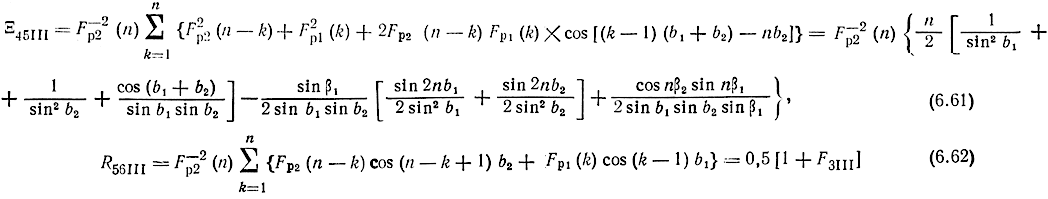
m принимает любое целое значение, например, n, n - k или k; Fp2(n) -совпадает с функцией расфазировки (5.151); Fh1,22(m) могут быть вычислены по формуле (6.29) или с помощью графиков рис. 6.3 при α1 = 0, если место β взять β1,2; X56II (b1,2)-функции (6.60), в которых β заменяется на b1,2.
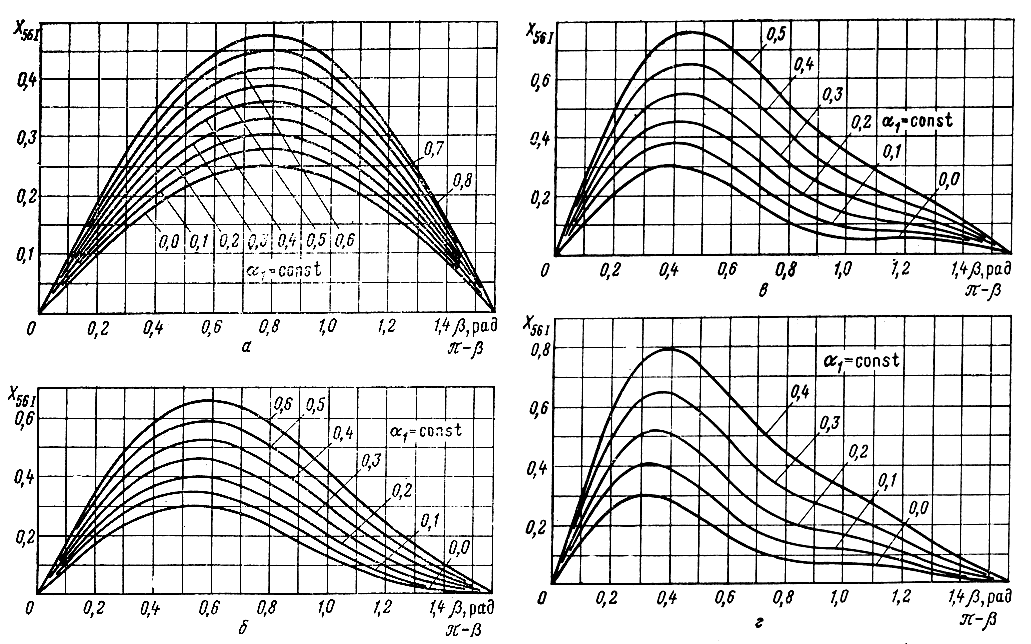
Рис. 6.6. Зависимости функции X56 от фазовой постоянной при различных значениях собственного затухания фильтров входной линии и n: а) n = 2; б) n = 3; в) n = 4; г) n = 5
Расчеты на ЭЦВМ и анализ (6.61)-(-6.63) показывают, что все слагаемые FH увеличиваются с увеличением расфазировки. Отсюда следует вывод о нецелесообразности применения способа расфазировки для выравнивания АЧХ ,в каскаде УРУ, предназначенном для усиления с малым коэффициентом шума.
Анализ приведенных формул и графических зависимостей, а также расчет составляющих FH конкретных схем каскада УРУ показывают, что коэффициент шума с увеличением частоты вначале уменьшается, а затем увеличивается, т. е. в середине полосы пропускания имеет место минимум. Если потери в ПЛ большие или для данного диапазона частот взят сравнительно низкочастотный УЭ, то минимум Fш имеет место в начале диапазона. Если потери небольшие и передающие линии достаточно хорошо сфазированы, то коэффициент шума при увеличении частоты уменьшается или остается приблизительно постоянным и только в конце диапазона (на частотах, близких к частоте среза) начинается быстрый подъем Fш. Вопрос оптимизации частотной зависимости Fш является весьма сложным, а на этапе общего анализа практически невозможен.
Для быстрой количественной оценки составляющих коэффициента шума (и их слагаемых) конкретных схем УРУ приведем инженерные формулы для частот, на которых β = 0, α1 = 0 и β = π/2, α1 ≠ 0 (табл. 6.1). Например, при использовании ФНЧ типа k данные значения соответствуют низким частотам и f/fcр = 0,7. При β = 0 потери обычно можно не учитывать. В том и другом случае расфазировка ПЛ считается пренебрежимо малой.

Таблица 6.1

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
