9.3. Динамический диапазон по комбинационным составляющим каскадов различных структур

Динамический диапазон по комбинационным составляющим второго и третьего порядка определяется по формуле (1.11) или как отношение амплитуд напряжений

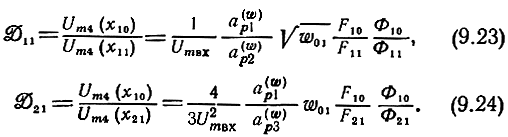
Следует заметить, что поскольку динамический диапазон, как правило, измеряется в децибелах, то определение его как отношение мощностей равноправно определению в виде отношения амплитуд напряжений.

Рассмотрим влияние частотных зависимостей волновых сопротивлений ПЛ каскада на изменение динамического диапазона в рабочей полосе частот, которое определяется сомножителем

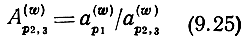
в выражениях (9.23), (9.24). Относительное изменение D, обусловленное изменением волновых сопротивлений, характеризуется отношением

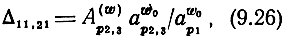
где индекс (w₀) означает нормировку коэффициентов относительно волновых сопротивлений на низкой частоте.

В табл. 9.1 приведены возможные варианты включения входа и выхода УЭ в соответствующие сечения фильтров, обозначаемые, например, как Т-П, что означает: вход УЭ подключен в Т-образное сечение, а выход в П-образное сечение фильтра. Для различных структур УРУ приведены общие формулы развернутого выражения (9.26), а также частные формулы для случая включения УЭ в П-П-образное сечение ФНЧ типа k. Индексы (01), (10), (И) и (21) над w_В в таблице означают волновые сопротивления на соответствующих частотах.

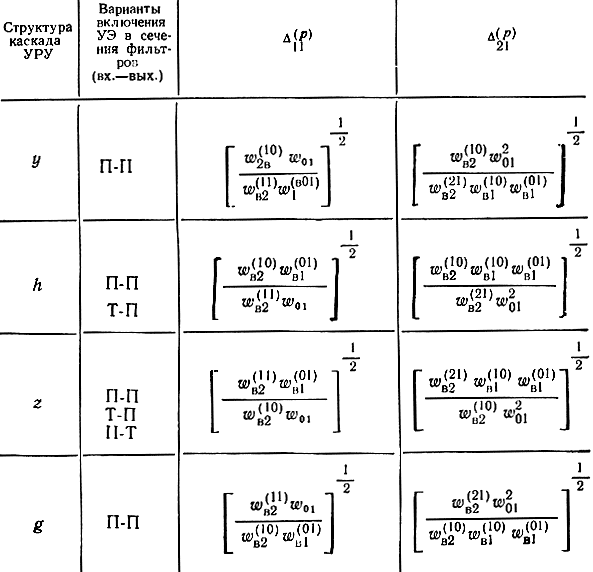
Таблица 9.1а. Общие формулы для Δ

Примечание: при включении в П-сечение w_B = w_Π, при включении р Т-сечение w_В = w_Н.

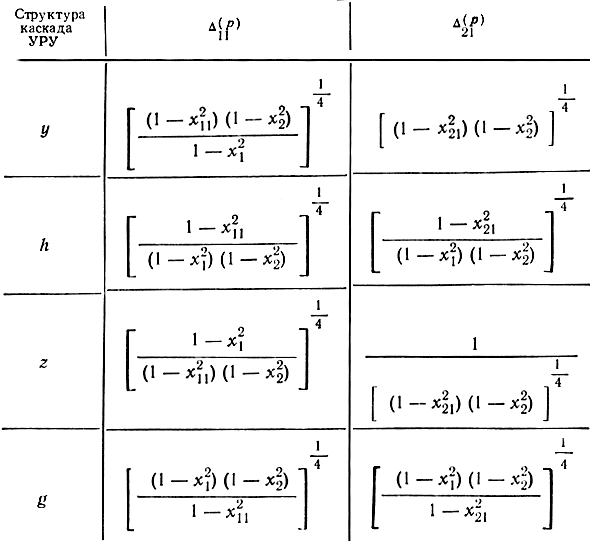
Таблица 9.1б. Формулы для Δ = f(х) при включении УЭ в П-П-образные сечения ФНЧ типа k

Из рассмотрения полученных результатов можно сделать следующие выводы. Частотная зависимость волновых сопротивлений звеньев передающих линий приводит к неравномерности величины нелинейных искажений в рабочем диапазоне частот усилителя. Для УРУ y и h - структур при включении УЭ в П-П-образные сечения фильтров величина D_qp с ростом комбинационной частоты (x_qp = qx₁ ± px₂) уменьшается. Величина D_oq, измеренная на одной и той же комбинационной частоте, зависит от соотношения испытательных частот x₁/x₂ и изменяется в пределах 6 дБ. В целом неравномерность величины D_pq в рабочем диапазоне частот составляет 9 дБ. С точки зрения характера неравномерности предпочтительным является усилитель h-структуры, так как в большей части частотного диапазона неравномерность носит положительный характер (величина D_pq возрастает). На величину динамического диапазона по комбинационным составляющим положительно влияют частотные свойства передающих линий в каскаде z-структуры при включении УЭ в П-П и П-Т-образные сечения фильтров.

Оценим влияние фазовой характеристики на величину нелинейных искажений. При линейной фазовой характеристике, когда β₁(x) = β₂(x) = сх, где c = const, как видно из выражений (9.14) -(9.16) β_qp = 0, а Φ_qp = 1. При изменении фазы по нелинейному закону β/2 = arcsin х и отсутствии расфазировки между линиями Φ₁₀ = 1, а Φ₁₁ и Φ₂₁ могут отличаться от единицы. Определим наибольшее значение фазовой постоянной 0,5β₁₁, когда одна из частот, например, x₁₁ = 0,9, а две другие связаны равенством x₁ = 0,9 - х₂. Из (9.15) β₁₁ = β₁(x₁) + β₁(x₂) - β₂(x₁₁) или

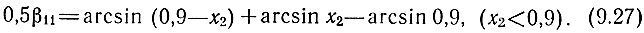
Разлагая в степенной ряд правую часть (9.27) и ограничиваясь первыми двумя слагаемыми, находим максимальное значение 0,5β₁₁, которое оказывается равным 10°40' при х₁ = х₂ = 0,45. Например, при α₁ = 0 и n = 5 можно практически считать, что влияние фазовой характеристики наибольшее и составляет 1 /Φ₁₁ = 1,14 (1,2 дБ). Расфазировка для комбинации x₂₁ = 0,9 достигает примерно той же величины при образующих частотах x₁ = 0,5 и x₂ = 0,1. На рис. 9.2 приведены графики зависимостей 1 /Φ₁₁ и 1/Φ₂₁ от си при различных, n для случая, когда 0,5β₂₁ ≈ 0,5β₁₁ = 10°40'.

Как видно из графиков, влияние фазовой функции на величину динамического диапазона увеличивается с ростом числа секций и уменьшается с возрастанием потерь во входной линии. Обычно УРУ состоят из трех-четырех секций, а потери во входной линии отличны от нуля (α₁ ≠ 0). Поэтому на практике влиянием фазовой функции на величину динамического диапазона (которая < 1дБ) можно пренебречь, а фазовую характеристику можно считать линейной, т. е. β₁(x) = β₂(х) = сх. Это позволяет на основании выражений (9.14) - (9.16) сделать следующий вывод: если в каскаде УРУ выполняются фазовые соотношения для частоты полезного сигнала, то они практически будут выполняться и для продуктов нелинейного преобразования, в результате чего на выходе усилителя будет иметь место синфазное сложение соответствующих комбинационных составляющих от различных УЭ.

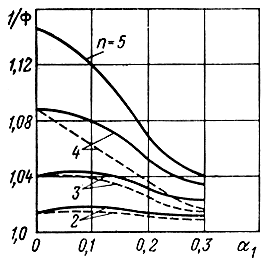
Рис. 9.2. Изменение фазовой функции в зависимости от собственного затухания и числа секций: ______ 1/Φ_u; - - - 1/Φ₂₁

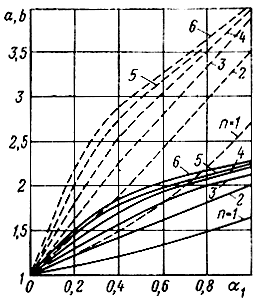
Рис. 9.3. Зависимости отношений функций потерь от собственного затухания и числа секций: _________ a = F(n, α₁)/F(n, 2α₁); - - - b = F(n, α₁)/F(n, 3α₁)

Рассмотрим влияние потерь на величину НИ. Из выражений (9.20), (9.23), (9.24) видно, что при отсутствии потерь в передающих линиях динамический диапазон по комбинационным составляющим не зависит от числа усилительных элементов n, так как lim_α1→0 (F₁₀/F_11,22) → 1 и определяется лишь величиной коэффициентов аппроксимации вольт-амперной характеристики, входного напряжения, частотно-зависимыми свойствами волнового сопротивления входной линии и фазовой характеристикой. При наличии потерь во входной линии (α₁ ≠ 0) D₁₁ и D₂₁ растут с увеличением n и α₁. На рис. 9.3 приведены зависимости отношений a = F(n, α₁)/F(n, 2α₁) и b = F(n, α₁)/F(n, 3α₁) от величины потерь и числа секций при близких частотах ω₁ и ω₂ (9.22). Рассматривая кривые, приходим к заключению, что при α₁ ≠ 0 рост динамического диапазона за счет увеличения числа УЭ ограничен. Увеличивать потери для получения максимального D_j нецелесообразно, так как это приведет к уменьшению коэффициента усиления УРУ. Поэтому при наличии потерь во входной линии к вопросу о выборе оптимального числа УЭ n_opt надо подходить из условия равномерности АЧХ усилителя. Полагая, что затухание во входной линии изменяется в соответствии с формулой 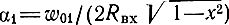, где R_BX - активная составляющая входного сопротивления УЭ, и используя приведенные графики, можно оценить влияние потерь на величину НИ в рабочем диапазоне частот.

Для величин D₁₁ и D₂₁ с отрицательной неравномерностью потери во входной линии и нелинейность фазовой характеристики УРУ играют роль корректирующих факторов.