3.2. Низкочастотная модель. Эквивалентные схемы. Методы расчета параметров ГГ

В области низких частот, где размеры громкоговорителя существенно меньше длины волны в воздухе d_ГГ << λ, и колебания диафрагмы носят поршневой характер, для анализа процессов преобразования сигнала в ГГ используется метод электромеханических аналогий. Теория этого метода постоянно совершенствуется, разрабатываются его прикладные приложения для расчета и проектирования электроакустических преобразователей (громкоговорителей, микрофонов, телефонов и т. д.). В его основе лежит сходство уравнений колебаний механических систем и электрических цепей, позволяющее установить соответствие между элементами электрической цепи и параметрами механической системы, если она может быть представлена системой с сосредоточенными параметрами, т. е. с конечным числом степеней свободы [45]. Поскольку электродинамический громкоговоритель представляет собой электромеханоакустический преобразователь, можно считать, что в области низких частот он содержит три типа сосредоточенных элементов: акустические, механические, электрические, поэтому для анализа его работы могут использоваться эквивалентные акустические, механические или электрические схемы, представляющие во всех случаях электрические цепи, элементы которых соответствуют определенному типу элементов ГГ (они могут с помощью соответствующих коэффициентов переводиться друг в друга) [25]. Принципы построения эквивалентных схем громкоговорителей детально рассмотрены в [5, 25, 45], поэтому приведем только некоторые основные соотношения для ГГ, полученные на основе разработанных за последние годы методов анализа и синтеза параметров акустических систем в области низких частот (теория Small-Thiele).

Развитие техники высококачественной аппаратуры категории HI-FI потребовало пересмотра подходов к разработке акустических систем, а именно перехода к их системному проектированию. Основа метода заключается в том, что электромеханические параметры низкочастотного громкоговорителя, конструктивные параметры корпуса и электрические параметры корректирующих цепей рассматриваются совместно и требования к каждому элементу определяются из общих требований на акустическую систему в целом на основе анализа ее обобщенной эквивалентной схемы. Такой подход оказался на практике значительно более эффективным в улучшении объективных характеристик и качества звучания АС, чем существовавшая ранее практика отдельного проектирования ГГ, корпусов и фильтров. Теоретической основой такого подхода явилось проведение аналогий между характеристиками эквивалентных схем, описывающих работу АС в области низких частот и характеристиками соответствующих электрических фильтров, что позволило применить хорошо разработанные методы анализа и оптимального синтеза фильтров к оптимизации параметров всех элементов АС, в том числе и громкоговорителей. Именно это направление в проектировании АС и ГГ с использованием ЭВМ интенсивно развивается в настоящее время.

Обобщенная эквивалентная акустическая схема ГГ в корпусе (учтены только наиболее распространенные типы оформления: закрытое, с фазоинвертором, с пассивным излучателем) показана на рис. 3.3, а. В данной схеме напряжения соответствуют звуковым давлениям, а токи - объемным скоростям, поэтому расчет токов и напряжений обычными методами теории цепей позволяет определить основные характеристики акустической системы - АЧХ, ФЧХ, КПД и др., а отсюда и требуемые параметры ГГ и корпуса. Для анализа электрических схем обычно используется понятие передаточной функции. Последняя может быть определена как отношение комплексного выходного сигнала, т. е. звукового давления p_вых(s) к комплексному входному сигналу, т. е. напряжению U_вх(s), H(s) = p_вых(s)/U_вх(s) (s - комплексная частота). Как известно, из теории цепей передаточная функция любой линейной системы может быть аппроксимирована дробно-рациональной функцией типа H(s) = W_m(s)/G(s) (W_m(s), G(s) - полиномы степени m и n, m ≥ n). Анализ эквивалентных акустических схем показывает, что, например, для закрытых АС (без корректирующих цепей) передаточная функция может быть аппроксимирована в виде

где А₁, a₀, а₁, а₂ - коэффициенты, зависящие от электромеханических параметров ГГ и корпуса. Вид этой функции аналогичен передаточной функции фильтра верхних частот полиномиального типа второго порядка (со спадом 12 дБ/окт в сторону низких частот). Для АС фазоинверсного типа функция H(s) имеет более сложный вид [5] и соответствует передаточным функциям фильтров четвертого порядка.

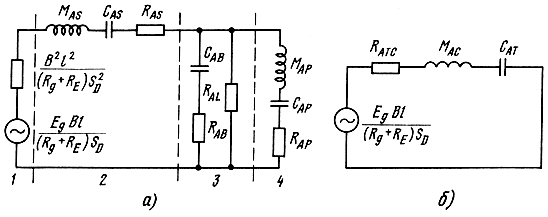
Рис. 3.3. Эквивалентная акустическая схема громкоговорителя в корпусе (а), эквивалентная акустическая схема громкоговорителя в закрытом оформлении (б): 1 - источник сигнала, 2 - громкоговоритель, 3 - корпус, 4 - фазоинвертор или пассивный излучатель

Из выражения (3.1) для передаточной функции можно определить АЧХ, ФЧХ, ГВЗ и КПД акустической системы:

где Re[H(s)], Im[H(s)] - реальная и мнимая части передаточной функции H(s). В условиях свободного поля КПД выражается через H(s):

где R_E - активное сопротивление, M_MS, S_D - механическая масса и площадь диффузора, Вl - коэффициент электромеханической связи в ГГ, ρ₀с - плотность и скорость звука в воздухе. В области частот, где АЧХ выходит на плоский участок, т. е. |H(s)| = 1

Задавая определенные требования к выходным характеристикам АС, можно с помощью анализа эквивалентных схем синтезировать требования к параметрам ГГ.

Рассмотрим синтез требований к параметрам низкочастотного громкоговорителя на примере АС с закрытым оформлением (рис. 3.3, б). Определенная из эквивалентной схемы передаточная функция имеет следующий вид:

где C_AT = C_ABC_AS/(C_AB + C_AS) - акустическая гибкость ГГ в закрытом корпусе; ω_C = 2πf_с = 1/Т_C = (С_АТМ_АС)^-0,5 - резонансная частота ГГ в закрытом корпусе; Q_TC = Q_ECQ_MC/(Q_EC + Q_MC) = 1/(ω_CC_ATR_AT) - полная добротность ГГ в закрытом корпусе; R_AT(R_AB + R_AS + B²l²)/(R_g + R_E)S²_D - активное сопротивление потерь в корпусе; R_AS - акустическое сопротивление потерь в подвижной системе; Q_MS = 1/(R_ATC_ATω_C) - механическая добротность ГГ в закрытом корпусе; Q_EC = ω_CR_EM_ACS²_D - электрическая добротность в закрытом корпусе; α = C_AS/C_AB - отношение гибкости подвеса C_AS и гибкости воздуха в закрытом ящике С_АВ. Поскольку гибкость воздуха в закрытом ящике пропорциональна V_B, α = V_AS/V_B, где V_AS - эквивалентный объем, V_B - внутренний объем корпуса.

Основными требованиями, задаваемыми при проектировании высококачественных акустических систем, является форма АЧХ в области низких частот, которая выбирается из совокупности требований к уровню линейных (фазовых, переходных и др.), нелинейных искажений и качеству звучания АС. Выбранная форма АЧХ аппроксимируется с помощью передаточной функции фильтра верхних частот определенного типа (например, Баттерворта, Чебышева и т. д.). При известном типе передаточной функции форма АЧХ может быть описана двумя параметрами Q_TC И f_C - полной добротностью и резонансной частотой. Например, вид АЧХ для АС закрытого типа (что соответствует передаточным функциям фильтра Баттерворта второго порядка) при разных значениях добротности показан на рис. 3.4. Обычно в требованиях на АС приводится нижняя граничная частота f_N при заданной неравномерности N. Эта частота может быть пересчитана в f_C по формуле, приведенной ниже. Кроме того, должен быть задан или максимальный объем АС V_B или требуемый КПД η₀ (может быть задан соответствующий ему уровень характеристической чувствительности S). Следует отметить, что эти величины не могут задаваться произвольно, так как для закрытых АС они связаны следующим предельным соотношением:

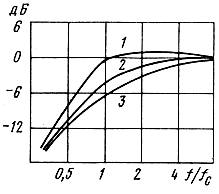
Рис. 3.4. Вид АЧХ при разных значениях добротности: 1 - Q = 1; 2 - Q = 0,707; 3 - Q = 0,5

Уровень характеристической чувствительности определяется через КПД соотношением: S = 20lg[(η₀ρ₀c/4π)^0,5/2⋅10^-5], поэтому (3.4) связывает допустимые значения объема V_B, граничной частоты f₃ (т. е. значение частоты на уровне -3 дБ от стационарного уровня) и уровня характеристической чувствительности S.

Наконец, для расчетов необходимо задать максимальный уровень звукового давления (max SPL) или максимально допустимую электрическую мощность Р_Emax (эти величины выбираются из требований на нелинейные искажения, а также механическую и тепловую прочность АС).

Перед началом расчета необходимо принять некоторые реальные значения α и Q_MC. Для компрессионных закрытых АС отношение гибкостей α должно быть больше 3. Обычно α выбирается 3...10 (как показал опыт расчетов АС, выбор значений в этих пределах некритичен для расчета параметров ГГ), значение Q_MS для закрытых АС рекомендуется выбирать равным 5. По вышеперечисленным параметрам акустической системы рассчитываются электромеханические параметры низкочастотного громкоговорителя.

Рассмотрим этот процесс на примере расчета параметров низкочастотного громкоговорителя по заданным требованиям к закрытой АС нулевой категории: требуемая (например, гладкая в области низких частот) форма АЧХ аппроксимируется передаточной функцией фильтра Баттерворта второго порядка с общей добротностью Q_TC = 0,707, нижняя граничная частота f_N = 31,5 Гц с неравномерностью N = -12 дБ; уровень характеристической чувствительности 88 дБ (можно было бы задать максимально допустимый внутренний объем, в данном случае 65 дм³); максимальный уровень звукового давления 110 дБ.

На первом этапе определяется значение f_C по заданным значениям f_N:

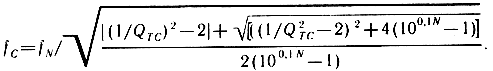
Значения f_C при f_N = 31,5 Гц и N = -12 дБ оказываются равными 61,8 Гц. Затем по (3.3) рассчитывается значение электрической добротности: при Q_MC = 5 и Q_TC = 0,707 Q_EC получается равной 0,823. Из соотношения Q_TC/Q_TS ≈ Q_EC/Q_ES ≈ f_C/f_S ≈ √(α + 1) определяется резонансная частота ГГ без оформления (при α = 4), f_S = 27,7 Гц и его электрическая добротность Q_ES = 0,368. По заданному значению характеристической чувствительности S = 88 дБ определяется значение КПД: η₀ = 0,758%. Поскольку формула для КПД для ГГ в закрытом корпусе может быть преобразована к виду [5]: η₀ = 2π²f³_CV_AT/(c³Q_EC), где V_АT = ρ₀c²С_АТ, то пользуясь этой формулой и соотношением V_АT = V_ASV_B/(V_AS + V_B), можно определить эквивалентный и внутренний объемы V_AS = 270 дм³ и V_B = 65 дм³ (с учетом толщины стенок этот внутренний объем соответствует внешнему объему порядка 100 дм³).

Из выражения

p = [P_ARρ₀c/(4πr²)]^0,5 = [P_Eη₀ρ₀c/4πr²]^0,5,

связывающего величину звукового давления р, Па, на расстоянии r от громкоговорителя с акустической мощностью P_AR (в условиях свободного поля) и с электрической мощностью Р_E, можно по заданному уровню максимального звукового давления max SPL, равного 110 дБ, определить максимальную электрическую Р_E = 154 Вт и максимальную акустическую мощность P_AR = 1,23 Вт. Затем с помощью формулы

где |X(jω)|²_max = Q⁴_TC/(Q²_TC - 0,25), определяется максимально допустимое объемное смещение V_D = 0,621 ⋅ 10^-3 дм³.

Поскольку V_D = X_DmaxS_D, необходимо задать либо X_Dmax - максимально допустимое смещение подвижной системы, либо S_D - эффективную площадь громкоговорителя. Обычно при расчетах задается S_D - эффективная площадь ГГ: во-первых, потому, что размеры низкочастотных ГГ выбираются из ограниченного стандартизованного ряда: 200, 250, 315, 380 мм, во-вторых, статистический анализ серийно выпускаемых АС отечественных и зарубежных позволяет установить четкую корреляцию объема системы с размерами низкочастотного громкоговорителя (рис. 3.5, а). Для систем с объемом порядка 65 дм³ обычно используется ГГ диаметром 315 мм. Этот размер соответствует S_D = 5,76⋅10^-8 м² (связь внешнего диаметра и эквивалентного диаметра показана на рис. 3.5, б), что позволяет получить значение максимального смещения ГГ X_Dmax = 0,108 × 10^-1 м. Существует и другой подход, когда из заданного уровня нелинейных искажений задается допустимое максимальное смещение и из него определяется площадь ГГ. В итоге рассчитываются следующие параметры низкочастотного ГГ: механическая гибкость подвеса: C_MS = C_AS/S²_D = V_AS/ρ₀c²S²_D = 0,584⋅10^-3 м/Н; полная механическая масса: M_MS= 1/[(2πf_s)²C_MS] = 0,0567 кг; (без присоединенной массы M_MS = M_MS - (M_M1 + M_MB1]), M_M1 = 3,14r³_D; M_MB1 = 0,65πρ₀r³_D она оказывается равной М_МS = 0,0428 кГ); коэффициент электромеханической связи A(х₀). Таким образом, параметры рассчитываемого низкочастотного громкоговорителя оказываются равными: S_D = 5,76⋅10^-2 м² (D = 315 мм), f_S = 27,7 Гц, Q_ES = 0,368, X_Dmax = 10,8 мм, Р_Еmax = 154 Вт, P_ARmax =1,23 Вт, S = 88 дБ/Вт, η₀ = 0,758%, C_MS = 0,584⋅10^-3 м/H, M_MS = 0,0567 кг (М′_MS = 0,0428 кг), А(х₀) = 14,6 Тм, R = 8 Ом. Эти данные хорошо согласуются с измеренными электромеханическими параметрами низкочастотного громкоговорителя диаметром 315 мм (см. гл. 5).

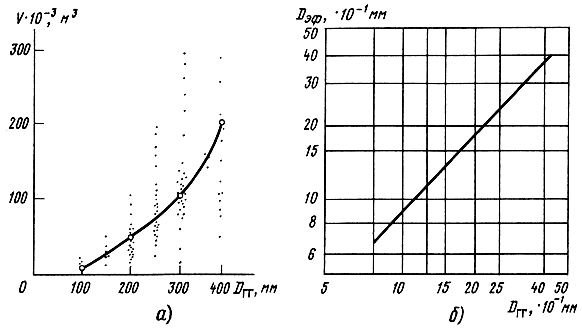
Рис. 3.5. Статистическая зависимость объема оформления V и диаметра диффузора D_ГГ (а); связь эффективного D_эф и выходного диаметра D_ГГ (б)

Аналогичная методика расчета параметров ГГ в корпусе с фазоинвертором приведена в [5, 25]. Как уже отмечалось, такой подход к расчету параметров громкоговорителей широко используется в отечественной и зарубежной практике разработок выносных АС, студийных агрегатов и т. д. Расчет параметров АС по заданным электромеханическим параметрам ГГ (в случае, если приходится разрабатывать АС под готовый громкоговоритель) изложен в [5, 25]. При проектировании массовых ГГ, каждый из которых применяется в нескольких видах аппаратуры, основные параметры задаются в техническом задании на разработку (перечень необходимых параметров задан в ОСТ4.383.001-85). В технической литературе имеется несколько различных вариантов методик расчета параметров массовых ГГ в области низких частот, позволяющих производить расчет из разных исходных предпосылок.

После определения вышеуказанных сосредоточенных параметров, выполненного на основе анализа соответствующих эквивалентных схем, необходима реализация следующего этапа - синтеза конструктивных параметров элементов подвижной системы (подвеса, диффузора, шайбы, звуковой катушки) и магнитной цепи. Решение этой проблемы представляет в настоящее время значительные трудности, прежде всего потому, что эта связь между полученными выше сосредоточенными параметрами (f_S, Q_ES, X_Dmax, C_MS, M_MS, A(X₀)) и конструктивными параметрами распределенных механических систем является неоднозначной, т. е. каждый из сосредоточенных параметров является функцией многих конструктивных переменных, например C_MS = C_MS(R, H, h, E, ρ и др.), т. е. гибкость зависит от глубины H, толщины h гофрировки на подвесе, модуля Юнга Е и плотности материала ρ и т. д. Поэтому одно и то же значение каждого из сосредоточенных элементов может быть реализовано с помощью различной совокупности конструктивных параметров. Кроме того, для установления этой зависимости необходимо решение комплекса задач, позволяющих установить аналитические или численные связи полученных сосредоточенных параметров с полным набором конструктивных параметров всех элементов ГГ. Состояние решения этих задач отражено в соответствующих разделах гл. 3. В настоящее время для этого используются различные приближенные методики, базирующиеся на имеющемся опыте разработок ГГ. Обычно по рассчитанным значениям электромеханических параметров подбирается конструкция ГГ, имеющая наиболее близкую совокупность измеренных параметров, она принимается за базовую и от нее с помощью созданных к настоящему времени методов с той или иной степенью приближения рассчитываются конструктивные параметры, затем конструкция экспериментально проверяется и доводится на моделях.