3.3. Процесс электромеханического преобразования сигнала в ГГ. Методы расчета параметров звуковых катушек и магнитных цепей

Как было показано в § 3.1, в подсистеме "магнитная цепь + звуковая катушка" происходит процесс электромеханического преобразования сигнала. Если рассматривать ГГ как преобразователь электрических колебаний в механические, то он может быть представлен в виде четырехполюсника (рис. 3.6, а), входные и выходные параметры которого описываются системой уравнений [45]:

где А - коэффициент электромеханической связи, Z_E - электрическое сопротивление, z_m - механическое сопротивление. С учетом специфики преобразования сигнала в электродинамических громкоговорителях (проводник с током в постоянном магнитном поле) коэффициент электромеханической связи А оказывается равным Вl [11], если ввести сосредоточенные электромеханические параметры громкоговорителя и значения коэффициента A, то схема рис. 3.6, а может быть приведена к виду, представленному на рис. 3.6, б. Из нее может быть получена как механическая эквивалентная схема ГГ (рис. 3.6, в), так и электрическая эквивалентная схема (рис. 3.6, г) путем соответствующего пересчета коэффициентов (акустическая эквивалентная схема приведена в § 3.2).

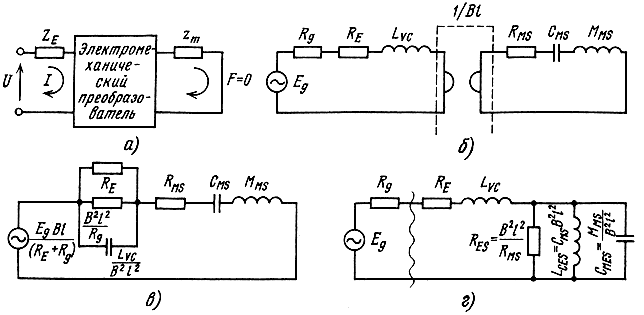
Рис. 3.6. Общая схема электромеханического преобразования сигнала (а), схема трансформации сигнала в ГГ (б), эквивалентная механическая схема (в), эквивалентная электрическая схема (г)

Полное электрическое сопротивление ГГ (без оформления), как следует из анализа его эквивалентных схем:

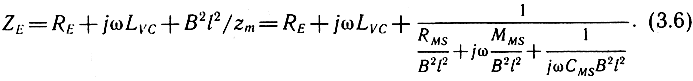
Форма амплитудно- и фазочастотной характеристики ГГ зависит как от упругих свойств подвижной системы, так и от частично-зависимого характера вынуждающей механической силы, который в значительной степени определяется функциональной зависимостью комплексного полного входного сопротивления от частоты Z_E(ω). Рассмотрим ее более подробно. Выражение (3.6) может быть преобразовано к виду:

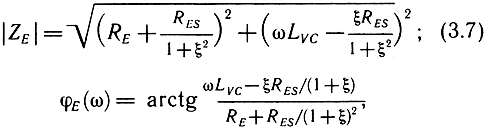
где |Z_E| - модуль полного входного сопротивления, φ_E - фазовый угол, Q_MS = R_E/ω_sL_CES; ξ = Q_MS(ω/ω_s - ω_s/ω); R_ES = B²l²/R_MS; L_CES = C_MSB₂l₂; C_MES = M_MS/B²l²; Q_MS - механическая добротность ГГ, ω_s =(1/L_CESC_LES) - частота механического резонанса. Характер зависимости модуля полного электрического сопротивления (АЧХ) и фазового угла (ФЧХ) от частоты показан на рис. 2.8. В области низких частот, где ω <ω>_s, система управляется в основном упругостью и Z_E ≈ (R_E + jωL_VC + jωC_MSB²l²). На частоте резонанса ω_s модуль |Z_E| достигает максимума, равного R_E + R_ES. Как следует из эквивалентной схемы (рис. 3.6), кроме резонанса на частоте ω_s данная электрическая цепь имеет резонанс на частоте ω_э = (ω²_S + 1/L_VCC_MES)^0,5. Эта частота называется частотой электромеханического резонанса, на ней модуль |Z_E| достигает своего минимального значения: |Z_E|_min = R_E + Δ, где

При этом Δ ≈ 0,1R_E, а ФЧХ проходит через нуль. В частотном диапазоне ω_S < ω < ω_э полное электрическое сопротивление носит емкостной характер, выше частоты ω > ω_э приобретает индуктивный характер и возрастает с повышением частоты, причем зависимость |Z_E| от частоты определяется в основном ростом индуктивности звуковой катушки L_VC. Поскольку увеличение |Z_E| приводит к уменьшению излучаемой мощности, для компенсации возрастания индуктивности звуковой катушки L_VC применяют различные конструктивные меры, в частности медные колпачки на керне и другие виды короткозамкнутых витков.

Таким образом, полное электрическое сопротивление Z_E имеет сложный характер частотной зависимости. Это приводит к тому, что даже при замене подвижной системы системой с сосредоточенными частотно-независимыми параметрами и подведением напряжения, не зависящего от частоты, амплитудно-частотная характеристика по звуковому давлению имеет вид, показанный на рис. 3.7.

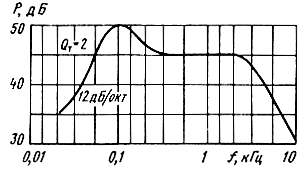
Рис. 3.7. Амплитудно-частотная характеристика поршневого излучателя (Q_T = 2)

В среднечастотной области, где находятся резонансные частоты колебаний диффузора, понятие сосредоточенных параметров становится неопределенным. Распределенная масса, гибкость и упругость диффузора имеют сложные характеры частотной зависимости (что соответственно определяет форму АЧХ и ФЧХ). Попытки построения эквивалентных схем для описания работы ГГ в этой области частот предпринимались неоднократно, например, использовались схемы в виде набора параллельных контуров [11]. Расширение частотного диапазона применимости эквивалентных схем и использование современных методов их оптимизации является актуальной проблемой в создании теории расчета ГГ (поскольку методы оптимизации в теории цепей значительно лучше разработаны, чем в теории механических систем), поэтому они активно развиваются в настоящее время с использованием теории идентификации.

Значительный вклад в формирование частотной зависимости электромеханической силы вносят конструктивные параметры звуковой катушки и магнитной цепи, поскольку процесс электромеханического преобразования происходит именно в этом узле ГГ. Исходными данными для их проектирования служат набор электромеханических параметров ГГ, полученный в § 3.2, а также ряд дополнительных требований по тепловой, механической прочностям и т. д. В практике проектирования серийных громкоговорителей используются в настоящее время достаточно хорошо опробированные методики инженерного расчета этих элементов ГГ. Остановимся на их рассмотрении более подробно.

Методы расчета параметров звуковой катушки. При выборе параметров ЗК разработчику приходится учитывать большой комплекс требований, основные из которых следующие: обеспечение заданного значения коэффициента электромеханической связи (полученное при расчетах электромеханических параметров ГГ исходя из общих требований к АС или параметров, заданных в техническом задании на ГГ, см. § 3.2); создание необходимых условий теплообмена исходя из подводимой к ГГ электрической мощности; обеспечение требуемых значений номинального электрического сопротивления; минимизация нелинейных искажений, возникающих при перемещениях ЗК в магнитном поле; оптимизация массы ЗК и обеспечение ее механический и климатической устойчивости.

Методики расчета параметров ЗК рассмотрены в [2, 45, 46], все они позволяют производить расчет с определенной степенью приближения и используются в настоящее время в практике разработок ГГ различного назначения. Исходными данными для расчетов параметров ЗК являются расчетная электрическая мощность Р_р, номинальное электрическое сопротивление R_н, коэффициент электромеханической связи А(х₀).

Расчетная электрическая мощность во всех вышеуказанных методиках принимается равной номинальной мощности ГГ с некоторым коэффициентом перегрузки К = 1,2...1,6. Учитывая, что в настоящее время номинальная мощность в стандартах на ГГ не указывается, а значения КР_н приближенно равны паспортной мощности Р_п, то в качестве расчетной мощности для массовых ГГ целесообразнее выбирать Р_п. При расчетах электромеханических параметров ГГ по методике, изложенной в § 3.2, задаются требования к максимальному звуковому давлению max SPL или максимальной электрической мощности, которая примерно соответствует Р_д.м - максимальной долговременной мощности (как показано в гл. 2, Р_{д. м} в 1,5...2 раза больше Р_п). Использование значений Р_{д. м} в качестве расчетной мощности требует значительного увеличения габаритов ЗК и магнитной цепи и может применяться только в особых случаях (при разработке мощных ГГ для специальных целей - озвучания больших помещений, концертно-театральной аппаратуры и т. д.).

Из заданного значения мощности Р_р определяется масса провода ЗК: m′_пр = (P_pγ)/(j²ρ) и его объем по металлу V′_пр = m′_пр/γ₃, где γ - плотность материала проводника (для меди 8,6 ⋅ 10³ кг/м³, для алюминия 2,5 ⋅ 10³ кг/м³); ρ - удельное сопротивление провода (для меди 1,75 ⋅ 10^-8 Ом/м, для алюминия 3,0 ⋅ 10^-8 Ом/м); j - плотность тока.

Катушка размещается внутри узкого зазора вблизи массивных металлических фланцев, поэтому условия охлаждения у нее относительно хорошие, что позволяет использовать высокие плотности тока. Результаты измерений серийных ГГ для бытовой радиоаппаратуры показали, что в них используются следующие значение j: для низкочастотных ГГ - 40...90 А/мм²; для высокочастотных - 80...120 А/мм², для широкополосных 50...100 А/мм².

Значение номинального электрического сопротивления R_H выбирается из стандартизованного ряда: 4, 8, 16, 25, 50 Ом. В бытовой акустической аппаратуре обычно используются ГГ с R_н = 4 или 8 Ом. Как уже было показано в гл. 2, обеспечение заданного значения R_H проверяется по измерению |Z|_min, которое не должно отличаться от R_H больше чем на 20%. Активное сопротивление ЗК R_E отличается от |Z|_min вследствие индуктивности катушки еще примерно в 1,1...1,4 раза. Поскольку для расчетов параметров ЗК необходимо исходя из заданных значений R_H выбрать допустимую величину R_E, практически допускать слишком низкое значение R_E невыгодно из-за ухудшения условий теплообмена (так как уменьшение R_E может быть выполнено за счет уменьшения длины провода, т. е. поверхности охлаждения, или увеличения его диаметра, т. е. ширины зазора). В то же время слишком большое значение R_E также нецелесообразно, так как при испытаниях напряжение, подводимое к ГГ, рассчитывается из заданного значения R_H и к ГГ, у которых выбраны слишком большие значения R_E, подводится меньший ток и, следовательно, получается меньший уровень звукового давления. В серийных ГГ обычно различие R_H и R_E, как показывает анализ статистических данных, составляет для низкочастотных ГГ примерно 20%, для высокочастотных 15%, для широкополосных 15%.

Из полученного значения сопротивления звуковой катушки R_E определяется длина провода l_п и диаметр провода d_п: R_E = (ρl_п)/q′ = (ρl_п)²/V′_пр(q′ = (πd′²_пр)/4 - сечение провода, V_пр = l_пq - объем провода). Отсюда: l_п = √(R_EV′_пр)/ρ и d′_пр = [(16ρV²_пр)π²R_E]^0,25. Исходя из рассчитанного значения d′_пр выбирается ближайшее нормированное значение диаметра провода d_пр и соответствующее значение диаметра провода в изоляции d_из. По полученным значениям корректируются сечение провода q, а также его объем и масса по формулам: V_пр = (q²R_E)/ρ; m′_пр = V_прγ. Эти величины используются в дальнейших расчетах.

Определение геометрических размеров и моточных данных ЗК (рис. 3.8) начинается с выбора числа слоев намотки N. Во всех серийно выпускаемых ГГ число слоев равно 2 (существует описание конструкций с числом слоев 3 и 4, однако они по различным технологическим причинам в серийных конструкциях не используются). При известном числе слоев могут быть определены толщина намотки ЗК: b_K = Nd_из и площадь ее цилиндрической боковой поверхности S_K = (V_пр/k_пр)b_K, где k_пр - коэффициент заполнения сечения катушки проводом. Коэффициент заполнения зависит от формы провода и толщины изоляции, он может быть увеличен за счет применения плоского прямоугольного провода.

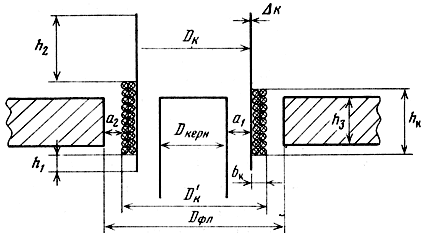
Рис. 3.8. Расчетная схема звуковой катушки

Для проверки условий охлаждения подсчитывается ориентировочная поверхность охлаждения: S″_охл и удельная мощность Р_уд = Р_р/S″_охл, при этом тепловой режим считается нормальным, если на каждую единицу мощности приходится определенная площадь боковой поверхности катушки. Статические данные для серийных ГГ показывают, что в низкочастотных ГГ используется 1/Р_уд = 0,42 ⋅ 10^-4 м²/Вт, в высокочастотных 0,9 ⋅ 10^-4 м²/Вт, в широкополосных 0,44 ⋅ 10^-4 м²/Вт. Величина S″ связана с величиной боковой поверхности катушки S_К (для бескаркасной намотки это соотношение может быть принято равным S″ = 2S_K, для теплопроводных каркасов S″ ≥ 2S_K, для нетеплопроводных S″ ≤ 2S_K).

Для расчета оставшихся размеров ЗК: среднего диаметра D_cp и высоты h_K необходимо определить радиальную ширину зазора магнитной цепи δ_З, диаметр керна D_кeрн и толщину верхнего фланца h_ф = h_З. Выбор этих величин в первую очередь диктуется требованиями к максимальной эффективности использования магнитного потока в конструкции магнитной цепи [47]. Эффективность определяется величиной коэффициента использования:

где В₃ - индукция в рабочем зазоре; V_З - объем зазора; (B_mH_m)_max - максимальное энергетическое произведение материала магнита, соответствующее оптимальной рабочей точке на кривой размагничивания; V_m - объем магнита. Как следует из (3.8), коэффициент χ зависит от отношения магнитной энергии в объеме рабочего зазора к максимальной магнитной энергии, которая может быть получена от магнита объемом V_m. Магнитный поток, развиваемый магнитом Ф_m, может быть представлен как Ф_m = Ф_З + Ф_рас, где Ф_З - магнитный поток в рабочем зазоре, Ф_рас - магнитный поток рассеяния. Если ввести коэффициент использования магнита по потоку:

где S_З - площадь рабочего зазора; S_m - площадь магнита, а также коэффициент использования магнита по магнитодвижущей силе к₂ = F_З/F_m = B_Зδ_З/H_ml_m, где δ_З - радиальная ширина рабочего зазора, l_m - длина магнита, то выражение (3.8) может быть преобразовано к виду:

Как следует из (3.10), коэффициент χ зависит от выбора рабочей точки В_mН_m на кривой размагничивания (чем ближе она к (B_mH_m)_max, тем больше значение χ), от коэффициентов использования к₁ - по потоку, к₂ - по магнитодвижущей силе и от значения B_mH_m)_max. Конструкции магнитных цепей, используемых в настоящее время, и значения к₁ и χ для них показаны на рис. 3.9. Как следует из этих данных, для всех используемых цепей к₁ ≤ 0,6. Наибольший к₁ имеют керновые цилиндрические магниты с плоским полюсным наконечником, однако в них не удается получить высокую индукцию в зазоре из-за ограниченности диаметра магнита. Магнитные цепи с кольцевыми ферритовыми магнитами имеют меньший коэффициент использования к = 0,3...0,35, однако они широко используются из-за низкой стоимости. Если считать, что практически весь магнитный поток проходит через керн, то выражение (3.9) может быть записано в виде к₁(S_кepнB_нac) = B_ЗS_З, где B_нac - индукция насыщения керна (для стали 10 она составляет примерно 1,5...2 Тл). Для определения по этому выражению диаметра керна необходимо задать значение индукции в зазоре В_З. Однако из результатов расчетов, полученных в § 3.2, определяется коэффициент электромеханической связи А(х₀), который связан с индукцией В_ср(х⁰), т. е. индукцией, усредненной по высоте катушки: А(х₀) = В_ср × (x₀)l_к. В этом случае выражение (3.9) следует преобразовать к виду π/4D²_кернB_нас = 1/к_пВ_ср(x₀)S_к, где к_п - коэффициент рассеяния по потоку, усредненному по высоте катушки (для кинотеатральных и мощных низкочастотных ГГ он составляет 0,6...0,8, для массовых к_п ≈ к₁). Отсюда диаметр керна

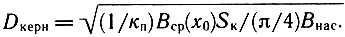
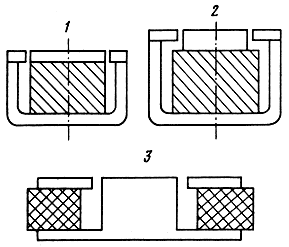
Рис. 3.9. Различные типы магнитных цепей: 1 - кернового типа - к₁ = 0,5...0,6; χ = 0,32...0,36; 2 - кернового типа к₁ = 0,4...0,45; χ = 0,22...0,32; 3 - кольцевого типа к₁ = 0,33...0,43; χ = 0,17...0,25

Полученные соотношения пригодны только для ненасыщенных магнитных цепей, однако стремление получить большую индукцию при минимальных габаритных размерах заставляет нередко использовать конструкции цепей с перенасыщенными магнитопроводами, особенно для малогабаритных массовых ГГ. В этом случае расчет коэффициентов рассеяния может производиться только численными методами на ЭВМ. Поскольку при серийном изготовлении ГГ керны изготавливаются из калиброванного стального прута, рассчитанный диаметр керна корректируется под соответствующий номинал (в массовых ГГ используются керны с диаметром 12, 15, 25 и 50 мм).

Основное влияние на коэффициенты рассеивания оказывает радиальная ширина рабочего зазора, при ее уменьшении возрастает доля полезного потока, увеличивается индукция в зазоре. Общая ширина зазора δ_З = b_к + Δ_к + a₁ + а₂, где b_к - ширина намотки катушки; Δ_к - толщина каркаса; а₁, а₂ - величина люфтов между катушкой и деталями магнитопровода (см. рис. 3.8). Если на керн одет медный колпачок, то ширина зазора увеличится на толщину колпачка. Толщина каркаса ЗК зависит от мощности ГГ и выбранного материала. В большинстве серийных ГГ используется для каркасов кабельная бумага, толщина которой составляет для массовых ГГ 0,08...0,12 мм (см. табл. 3.1). Величина люфтов выбирается на основе компромисса между стремлением увеличить индукцию в зазоре и увеличением числа бракованных ГГ из-за дребезжания, которое возрастает при малых люфтах. При современном уровне автоматизации производства величина а₁/а₂ составляет в среднем 0,15/0,3 для малогабаритных и 0,3/0,6 для больших ГГ (подробные данные приведены в табл. 3.1).

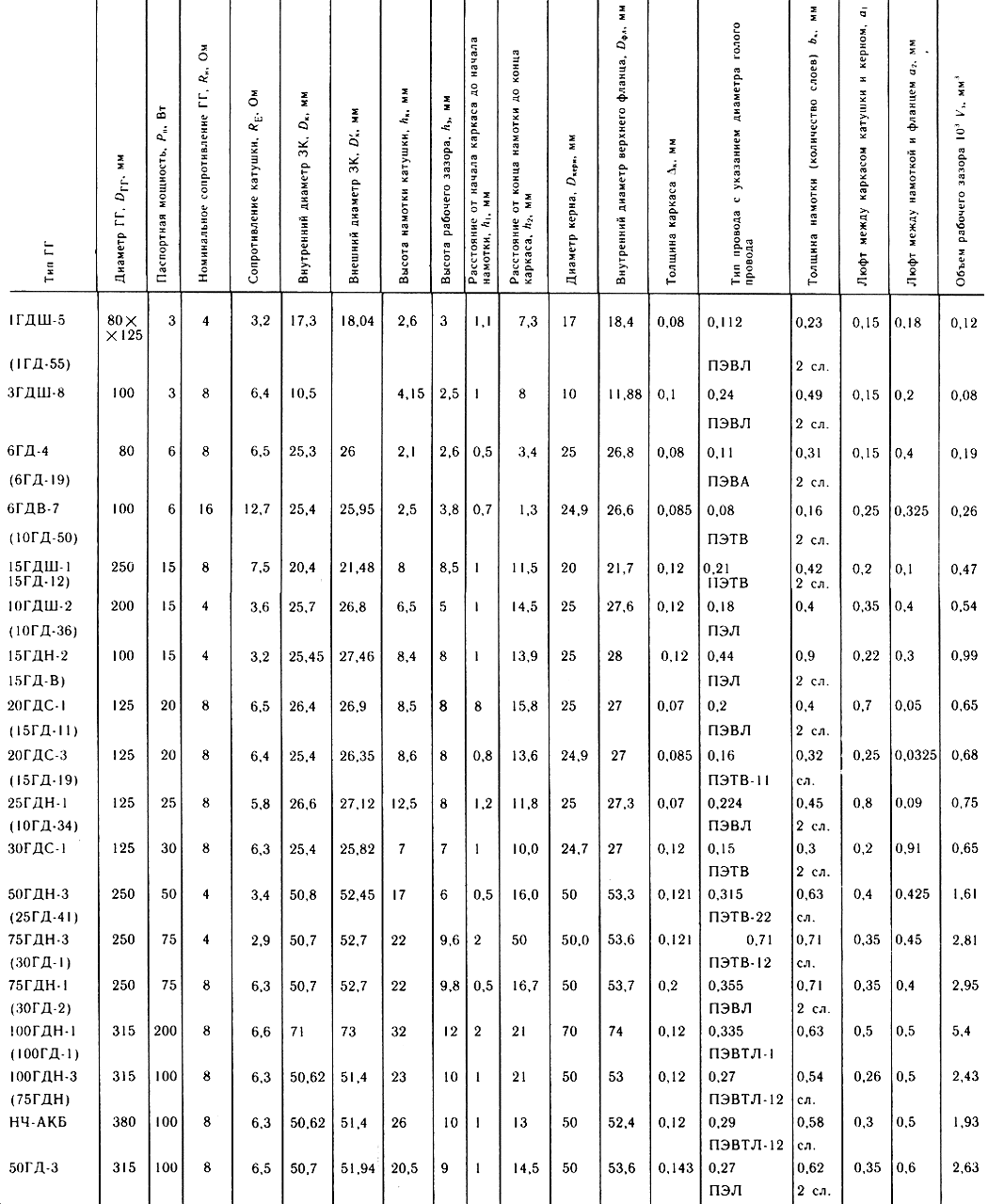
Таблица 3.1

После определения ширины зазора δ_З может быть определен средний диаметр звуковой катушки: D_ср = D_керн + 2(а₁ + Δ_К + b_к/2), и диаметр верхнего фланца: D_фл = D_керн + 2δ_З. В современных мощных ГГ при выборе диаметра катушки необходимо учитывать требования по обеспечению режимов теплообмена. Как показали исследования тепловых режимов работы ГГ, существует четкая корреляция между подводимой мощностью и диаметром ЗК, показанная в табл. 3.7 (см. § 3.9). Поэтому значения D_cp должны быть проверены в соответствии с табл. 3.7 и при необходимости откорректированы.

Из полученного значения D_cp уточняется высота намотки h_к и число витков в слое n: площадь боковой поверхности ЗК S_K = nπD_cph_K в то же время ее можно определить как S_K = l_Kd_из/n (l_к - длина провода). Из этих формул следует, что высота намотки h_K = S_K/πD_cp = l_кd_из/nπD_cp, общее число витков n = l_K/nπD_cp, при этом среднее число витков в слое n_cp = n/N (для двуслойных катушек обычно в первом слое n_ср + 1, во втором n_ср - 1).

Важнейшим параметром, влияющим на уровень нелинейных искажений, является отношение высоты катушки к высоте зазора. В [46] построены эмпирические зависимости высоты зазора от его радиальной ширины для определенных типов ГГ. В современных серийных ГГ для бытовой радиоаппаратуры используемые соотношения h_K/h_З даны в табл. 3.1. Анализ этих данных показывает, что в массовых ГГ используются следующие соотношения: для низкочастотных h_K/h_З = 2,0...2,4; для средне-частотных 1,2...1,4; для высокочастотных 1,0...1,2; для широкополосных 1...1,5. Величина h_K определяет высоту намотки ЗК, общая высота каркаса H_к выбирается из конструктивных соображений таким образом, чтобы обеспечить приклейку диффузора и шайбы в верхней части каркаса и оставить в нижней части примерно 1 мм. Расчет индуктивности ЗК выполняется по формулам, приведенным в § 3.8. Данные по конструкциям звуковых катушек для некоторых серийных ГГ приведены в табл. 3.1 (наименования ГГ приведены в новых и применяемых до настоящего времени обозначениях).

Приведенные выше соотношения могут быть проиллюстрированы на примере расчета звуковой катушки ГГ с электромеханическими параметрами, полученными в § 3.2: A(x₀) = 14,6 Тм; R_н = 8 ОМ; Р_maх = 150 ВТ (что соответствует P_п ≈ 100 Вт); масса провода m′_пp = (P_pγ/j²pρ) = 100 ⋅ 8,6 ⋅ 10³/6,8² ⋅ 10¹⁴ ⋅ 1,75 ⋅ 10^-8 = 10,6 ⋅ 10^-3 кг; объем провода по металлу V′_пp = m′_пp/γ = 10,6 ⋅ 10^-3/8,6 ⋅ 10³ = 1,23 ⋅ 10^-6 м³; сопротивление катушки R_E = R_H/к = 8/1,17 = 6,83 Ом; длина провода l_к = (R_EV_пp/ρ)^0,5 = (6,83 ⋅ 1,23 ⋅ 10^-6/1,75 ⋅ 10^-8)^0,5 = 22,0 м; диаметр провода без изоляции d′_пp = (16ρV′_пp/π²R_E)^0,25 = (16 ⋅ 1,75 ⋅ 10^-8 ⋅ 1,23 ⋅ 10^-6/лπ² ⋅ 6,83)^0,25 = 0,27 ⋅ 10^-3 м; d_из = 0,3 ⋅ 10^-3 м; число слоев намотки N = 2; толщина намотки b_K = Nd_из = 2 ⋅ 0,31 ⋅ 10^-3 = 0,62 ⋅ 10^-3 м; площадь поверхности катушки S_K = V_пр/к_прb_к = 1,23 ⋅ 10^-6/0,59 ⋅ 0,62 ⋅ 10^-3 = 34,5 ⋅ 10^-4 м², где к_пр = π/4d²_пр/d²_из = π/4 × (0,27/0,31)² = 0,59; площадь поверхности охлаждения S″_oxл = 2S_K = 2 ⋅ 37 ⋅ 10^-4 = 69 ⋅ 10^-4 м²; удельная мощность 1/Р_уд = S″_охл/Р_р = 69 ⋅ 10^-4/100 = 69 ⋅ 10^-6 м²/Вт; Р_уд = 14,4 ⋅ 10³ Вт/м²; диаметр керна D_керн = [(1/к_п)(A(x₀)/l_к)S_к/(B_насπ/4)]^0,5 = (0,83 ⋅ 0,66 ⋅ 34,5 ⋅ 10^-4/l,5 ⋅ 0,78)^0,5 = 48 ⋅ 10^-3 м; D^H_керн = 50 ⋅ 10^-3 м; общая ширина рабочего зазора δ_З = b_к + Δ_к + а₁ + а₂ = (0,62 + 0,12 + 0,26 + 0,5) ⋅ 10^-3 = 1,5 ⋅ 10³ м; средний диаметр ЗК: D_cp = D_кepн + 2(a₁ + Δ_K + b_K/2) = 50 + 2(26 + 0,12 + 0,31) × 10^-2 = 5,138 ⋅ 10^-2 м; диаметр верхнего фланца (внутренний): D_фл = D_кepн + 26,δ = (50 + 2 ⋅ 1,5) ⋅ 10^-2 = 5,3 ⋅ 10^-2 м; число витков в катушке n = l_K/nπD_cp = 22,0/лπ ⋅ 51,38 ⋅ 10^-3 = 136; высота намотки h_K = S_K/nπD_cp = 34,5 ⋅ 10^-4/π ⋅ 51,38 × 10^-3 = 21,4 ⋅ 10^-3 м; число витков по слоям n₁ = 69; n₂ = 67; высота зазора: h₃ = h_к/2,3 = 9,3 ⋅ 10^-3 м.

Методы расчета параметров магнитной цепи. При проектировании конструкции магнитной цепи исходными являются следующие требования: обеспечение заданного значения индукции в рабочем зазоре при минимальном объеме магнита (поскольку постоянные магниты являются наиболее дорогим элементом в ГГ); обеспечение требований к полям рассеяния (так как в ряде случаев применения ГГ, например, в телевизорах, приемниках и другие требования к минимизации полей рассеяния являются чрезвычайно жесткими); снижение уровня нелинейных искажений за счет обеспечения соответствующего распределения постоянных и переменных магнитных полей; оптимизация тепловых режимов работы звуковой катушки в магнитных цепях ГГ.

Как уже было отмечено в гл. 1, практически во всех промышленных типах ГГ используются следующие типы магнитных цепей с постоянными магнитами: кернового типа (различные: варианты конструкций показаны на рис. 3.9), кольцевого типа с феррит-бариевыми магнитами (рис. 3.9 и в табл. 3.2) и кольцевого типа с литыми магнитами (см. рис. 1.2). Выбор типа цепи зависит от конструктивных и экономических требований: применение керновых цепей позволяет уменьшить габаритные размеры и снизить интенсивность полей рассеивания, однако они дороже и технологически сложнее в изготовлении, чем цепи с кольцевыми магнитами, поэтому применяются в основном для ГГ в телевизионной и переносной радиоприемной аппаратуре. Параметры применяемых в ГГ магнитомягких (магнитопроводов) и магнитотвердых (постоянных магнитов) материалов рассмотрены в гл. 4. Расчеты магнитных цепей выполняются в настоящее время как по приближенным методикам [47], так и точными численными методами на ЭВМ [48]. Приближенные методы расчета базируются на аналогиях между магнитными и электрическими цепями, по которым закон Ома для магнитной цепи может быть записан в виде: Ф_m = F_m/(R_m + R_н), где Ф_m - полный магнитный поток, проходящий через нейтральное сечение магнита, F_m - намагничивающая сила постоянного магнита, R_m, R_H - магнитные сопротивления соответственно магнитопровода и воздушных участков магнитной цепи. Магнитный поток, проходящий через нейтраль магнита, разветвляется в цепи на множество потоков рассеяния. В соответствии с этим схема электрического замещения магнитной цепи может быть представлена в виде параллельного соединения n ветвей, проводимости которых соответствуют магнитной проводимости различных путей магнитного потока. Часть создаваемого магнитного потока проходит через рабочий зазор (проводимость его g_δ), она называется полезным магнитным потоком. Остальная часть рассеивается внутри магнитной цепи и в окружающем пространстве. Доля полезного магнитного потока определяется соотношением проводимости g_δ и проводимостей рассеяния g₂, ..., g₁₁. Магнитная цепь с обозначением основных зон проводимости и ее схема замещения показаны на рис. 3.10.

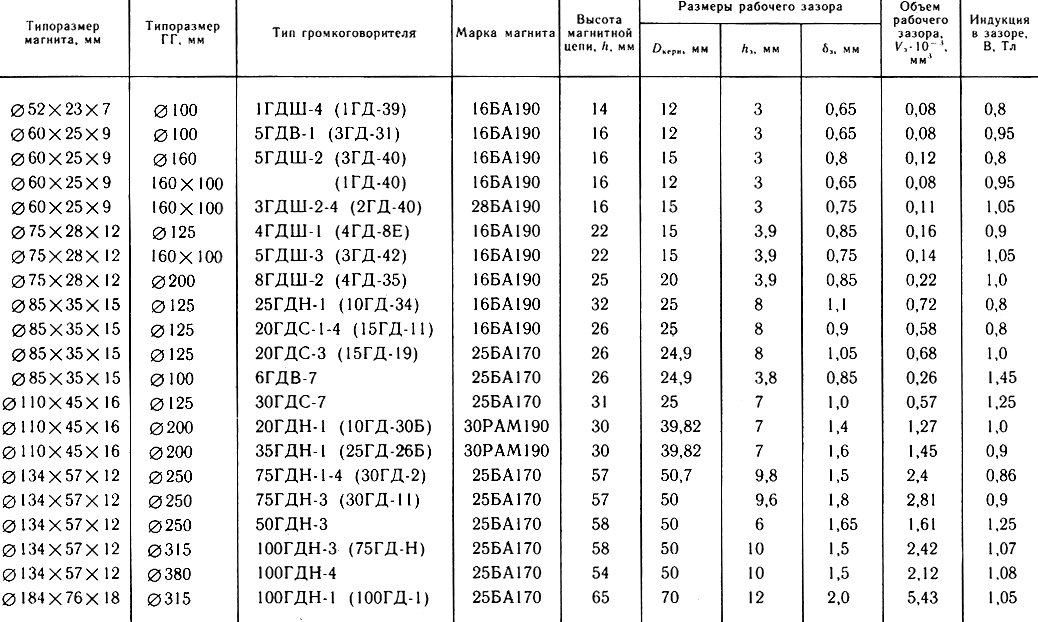
Таблица 3.2

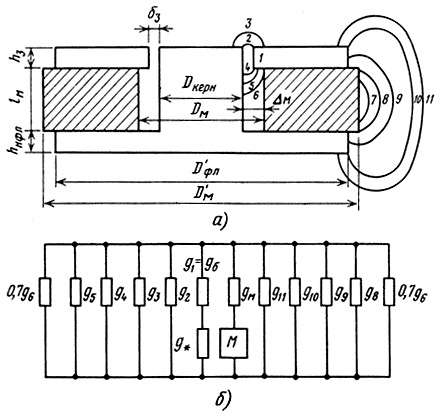
Рис. 3.10. Расчетная схема магнитной цепи (а), схема замещения (б)

Исходными данными, необходимыми для расчетов параметров магнитной цепи, являются: высота и радиальная ширина рабочего зазора h_З и δ_З; диаметр керна D_керн и требуемая расчетная индукция в зазоре В_З. Их значения могут быть заданы или получены в процессе проектирования звуковой катушки. Особо следует остановиться только на значениях индукции. При расчетах ГГ [46] используются различные значения индукции: В_л(х) - локальная индукция, т. е. индукция в заданном сечении зазора (такая величина получается в процессе измерений, например, с помощью датчиков Холла или расчетов магнитных полей численными методами на ЭВМ); В_ср(х) - индукция, усредненная в некоторой области (например, при расчетах ЗК используется значение индукции, усредненное по высоте катушки при любом ее положении в зазоре В_ср(x₀)). Связь полученных из расчетов ЗК значений В_ср(х₀) с необходимыми для расчетов магнитной цепи значениями В_З (т. е. значениями локальной индукции В_л(х), усредненными по высоте зазора) показана на рис. 3.11. Кроме того, необходимыми данными для расчетов являются параметры, полученные из представленных на рис. 4.5 кривых размагничивания применяемых в производстве ГГ марок магнитов (28РА 180, 25 БА 170, 22РА 220 и др.) и магнитопроводов (сталь 10).

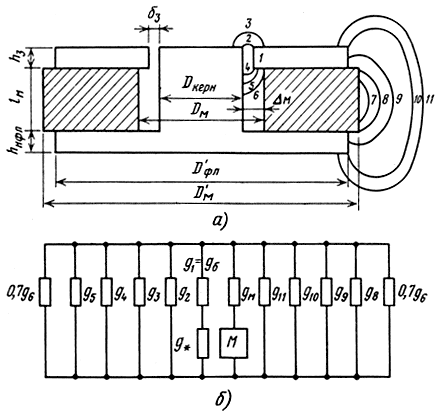
Рис. 3.11. Зависимость В_ср(х_с)/В_З от h_K/h_З

Процесс расчета магнитной цепи состоит из двух этапов. На первом этапе ставится задача определения наименьших размеров магнита, позволяющих обеспечить требуемую индукцию в рабочем зазоре. На втором этапе выбирается стандартизованный типоразмер магнита, ближайший к рассчитанному, и проверяется индукция, которую он может обеспечить. Расчет параметров магнитной цепи начинается с выбора на кривой размагничивания магнита рабочей точки с координатами Н_m и В_m (Н_m - напряженность поля, В_m - индукция). Обычно рабочая точка задается как можно ближе к оптимальной точке кривой размагничивания выбранного материала магнита, так как это соответствует максимальной удельной магнитной энергии и позволяет получить наименьший объем магнита для заданной индукции. Однако для феррит-бариевых магнитов выбор рабочей точки определяется тем, что их свойства сильно зависят от температуры [3.16]. Характер изменения кривых размагничивания при изменении температур в интервале +20...- 40°С показан на рис. 3.12. Если рабочая точка выбирается на участке кривой, находящейся выше оптимальной, то изменения магнитных свойств, наступившие при охлаждении магнита, при последующем повышении температуры, будут обратимыми.

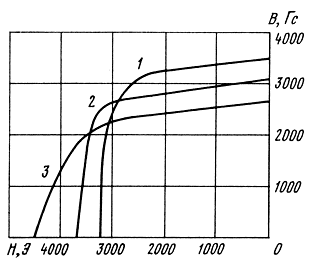
Рис. 3.12. Кривые размагничивания при разных Т°: 1 - Т = -40°; 2 - Т = +20°; 3 - Т = + 130°

Кроме того, феррит-бариевые магниты отличаются неоднородным распределением поля внутри магнита, поэтому магнитное состояние их характеризуется не одной точкой, а некоторой областью на кривой размагничивания. Выбор рабочей точки обычно производится для некоторой средней зоны магнита, при этом учитывается условие, чтобы для всех зон магнита рабочие точки были не ниже оптимальной, иначе в них могут иметь место необратимые температурные изменения. Все эти соображения заставляют выбирать рабочую точку для ферритовых магнитов несколько выше оптимальной. Для литых магнитов зависимость от температуры слабая и рабочая точка может практически совпадать с оптимальной. Дальнейший расчет выполняется методом последовательных приближений, различные процедуры расчета для литых керновых магнитов и кольцевых феррит-бариевых рассмотрены в [2, 46, 47].

Рассмотрим более подробно основные этапы расчета магнитных цепей с феррит-бариевыми магнитами по методике, имеющей наибольшее использование в практике расчетов промышленных типов ГГ. После выбора на кривой размагничивания рабочей точки с координатами H_m, В_m ориентировочно рассчитываются длины магнита l_m и поперечное сечение S_m:

где к - коэффициент потерь магнитодвижущей силы (МДС) на преодоление магнитного сопротивления магнитопровода (к = 1/к₂);

где S_З - площадь рабочего зазора, равная S_З = nπ(D_керн + δ_З)h_З; δ - коэффициент рассеяния магнитного потока (δ = 1/к₁). Начальные значения к и σ выбираются равными k = 1...2; σ = 2...3.

Далее определяется внешний диаметр магнита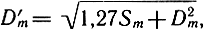  

где D_m - внутренний диаметр магнита, равный D_m = D_керн + 2Δ_m величина люфтов Δ_m выбирается обычно от 3 до 7 мм (см. табл. 3.1); и внешний диаметр фланца D′_фл = D′_m - l_m/2 (толщина нижнего фланца принимается равной толщине верхнего фланца h_фл = h_З). После этого для магнитной цепи с определенными выше параметрами производится расчет проводимостей по следующим формулам (см. рис. 3.10, а): рабочий зазор (участок 1): g_δ = π(D_керн + δ_З)h_З/δ_З;

участок 2: g₂ = 0,25π(D_керн + 2δ_З)δ_З;

участок 3: g₃ = (D_керн + δ_З)ln[(D_керн + 2δ_З)/δ_З];

участок 4: g₄ = 0,25π(D_керн + 2δ_З);

участок 5: g₅ = 2D_кeрнln[(D_m - D_керн)/2δ_З] + 4/π(D_m - D_кeрн - 2δ_З);

участок 6: g₆ = 2πl_m/{ln[(D_m + 0,4D′_m - 0,4D_m)]/D_кepн};

участок 7: g₇ = π^3/2l_mD′_m/S^0,5, где S = πD′l_m/2 + h₃πD′_фл + π/4[D′²_фл - (D_кepн + 2δ_З)²] + h₃π(D_керн + 2δ₃) + π(D_кeрн + 2δ₃)l_m/2;

участок 8: g₈ = 0,25πD′_фл;

участок 9: g₉ = π^3/2h_ЗD′_фл/S^0,5;

участок 10: g₁₀ = 0,25πD′_фл;

участок 11: g₁₁ = π^3/2[D′²_фл - (D_керн + 2δ_З)²]/4S^0,5.

Проводимость магнитопровода g_ж = S_K/(l_к/μ + γ) = π/4(D²_керн - d²_K)/(l_к/μ + γ), где γ - остаточный зазор в месте запрессовки керна, равный примерно 0,2 мм, l_к - длина керна l_к = l_m + h₃; μ - магнитная проницаемость материала керна; d_K - диаметр внутреннего отверстия в керне (если оно имеется в конструкции). Суммарная проводимость зазора и магнитопровода g′_δ = g_δg_ж/(g_δ + g_ж). Полная проводимость системы

По полученным значениям проводимостей вычисляется уточненное значение коэффициентов σ′ и к′: σ′ = Σg/g_δ,

где B_к - индукция в основании керна:

По уточненным значениям к′ и σ′ вновь рассчитываются размеры магнитной цепи S_m, l_m, D′_m, D′_фл, по ним пересчитываются значения проводимостей и определяются значения к″ и о″ во втором приближении. Цикл расчета повторяется до тех пор, пока разность между двумя последовательно вычисленными значениями l_m и S_m не станет меньше 0,01 ⋅ 10^-2 м (для l_m) и 10^-8 м² (для S_m). В результате расчета определяются минимальные размеры магнита, необходимые для обеспечения требуемой индукции в зазоре.

На втором этапе выбирается стандартизованный типоразмер магнита, ближайшего к вычисленному, и рассчитывается индукция в зазоре. Для реализации второго этапа расчета магнитной цепи созданы программы "Magnet" и "Realus" для ЭВМ типа СМ-4. Например, расчет по этим программам магнитной цепи с исходными данными: h₃ = 10 мм; δ₃ = 1,5 мм; D_кepн = 50 мм и B₃ = 1,07 Тл, магнит 25БА-170, магнитопровод - сталь 10 позволил получить следующие результаты: D_M = 57 MM, D″_M = 134 мм; l_m = 36 мм; S_m = 115,51 ⋅ 10² мм²; к = 1,324; σ = 1,917; B₃ = 1,138 Тл. Ближайший типоразмер был выбран со следующими размерами: D_M = 57 мм; D″_M = 134 мм, l_m = 24 мм. Уточненные значения величин с этими размерами оказались следующими: к = 1,158; σ = 1,83; В_cр = 1,1118 Тл. Следует отметить, что расчеты по этим приближенным методикам могут производиться только для ненасыщенных магнитных цепей со сравнительно простой конфигурацией. Более общие задачи расчета параметров магнитных цепей могут решаться только точными методами с помощью ЭВМ.

Бурный рост вычислительной техники за последние годы способствовал развитию численных методов расчета магнитных полей в цепях различной конфигурации [48]. Задача расчета характеристик постоянных магнитных полей сводится к решению уравнений Максвелла, которые для данного случая могут быть представлены в виде:

где Н - напряженность; В - индукция магнитного поля; М - намагниченность; μ - магнитная проницаемость. Задавая условия на границах различных сред (магниты, магнитопроводы, воздушные зазоры), можно свести задачу расчета магнитного поля к решению вариационной задачи минимизации функционала энергии, которая решается методом конечных элементов (МКЭ). Исходная область Ω покрывается регулярной треугольной сеткой (рис. 3.13, а), затем выбирается начальное приближение и организуется итерационный процесс. Созданный пакет программ для ЭВМ типа ЕС-1045 позволяет производить расчет распределения магнитных потоков в магнитных цепях, типичных для применения в ГГ керновых, кольцевых и других конфигураций. Пример расчета кольцевой магнитной цепи показан на рис. 3.13, б. Это дает возможность количественно оценить влияние конструктивных параметров (размеров и марки магнита и магнитопровода, высоты и ширины зазора, конфигурации фланцев и т. д.) на распределение магнитного потока в цепи. В настоящее время создаются программы для расчета переменных магнитных полей, индуцируемых током звуковой катушки, что дает возможность производить расчет нелинейных искажений, возникающих за счет взаимодействия постоянных и переменных полей, и тем самым оптимизировать конструкцию магнитной цепи с целью их минимизации. Параметры магнитных цепей с феррит-бариевыми магнитами ряда серийных ГГ показаны в табл. 3.2.

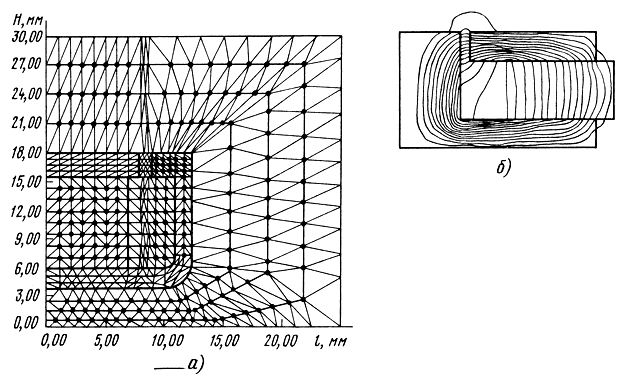
Рис. 3.13. Расчетная сетка (а) и распределение эквипотенциальных линий магнитного потока (б)