3.4. Линейные механические колебательные процессы в элементах подвижной системы ГГ

Общая структура колебательных процессов и ее связь с формой АЧХ. Как было показано в § 3.1, в следующей подсистеме - "подвижная система громкоговорителя" в электродинамических ГГ механическая сила F(t) преобразуется в распределенные механические смещения в элементах подвижной системы. Последняя представляет собой совокупность различных оболочек вращения (подвес, диффузор, шайба, колпачок, катушка), которые под действием приложенной силы совершают вынужденные линейные и нелинейные колебания. Структура распределения амплитуд и фаз смещений на поверхности диффузоров и подвесов (основных элементов подвижной системы) является определяющим фактором в формировании амплитудно- и фазочастотных характеристик ГГ (естественно, распределение смещения на поверхности корпуса, в котором установлен ГГ, также вносит свой вклад в формирование АЧХ и ФЧХ в области низких и средних частот). Исследование структуры распределения колебаний на поверхности диффузоров и подвесов и установление ее связи с формой АЧХ проводились на протяжении всего длительного периода развития производства ГГ. Применение современной измерительной техники, в частности голографической интерферометрии (см. гл. 2), позволило к настоящему времени получить следующие результаты.

Если рассмотреть типичную форму АЧХ широкополосного ГГ средних размеров (например, на рис. 3.14 показана форма АЧХ для ГГ диаметром 152 мм) и сопоставить ее с распределением структуры колебаний на поверхности диффузоров и подвесов, то можно выделить характерные частотные области:

область низких частот I - от нижней частоты воспроизводимого диапазона до частоты примерно 300...400 Гц для конусных ГГ средних размеров (с уменьшением диаметра ГГ эта частота увеличивается), колебания диффузоров носят поршневой характер (рис. 3.15, а, б), основное влияние на форму АЧХ и ФЧХ оказывают резонансные колебания подвесов, зависящие от их конструктивных и физико-механических параметров;

область средних частот II - примерно 300...1000 Гц, на диффузоре формируется волновая картина распределения амплитуд и фаз с радиальными узловыми линиями (рис. 3.16, а, б), по мере повышения частоты число волн по окружности возрастает от 4 до 8, причем устанавливаются они на некотором расстоянии от катушки ближе к подвесу. Следует отметить, что четкая волновая картина образуется только на дискретных резонансных частотах, между этими частотами волновая картина становится нечеткой и амплитуды значительно уменьшаются. Этот вид резонансных колебаний с радиальными узловыми линиями носит паразитный характер, так как в силу их симметричности радиальные резонансы компенсируют друг друга и мало влияют на форму АЧХ на оси. Однако при нарушении однородности диффузоров, перекосов при сборке симметричность нарушается и эти резонансы могут оказывать существенное влияние на неравномерность АЧХ, измеренной на оси и под углами, и уровень нелинейных искажений. Для борьбы с этими резонансами используют различные методы повышения жесткости диффузоров в окружном направлении: за счет направленной укладки бумажных волокон при отливке, нанесения кольцевых ребер жесткости, применения анизотропных материалов и т. д. В частности, влияние направленной укладки волокон вдоль окружности, проверенное на партиях серийных диффузоров, показало, что оно позволяет увеличить модуль Юнга в 1,5-2 раза в окружном направлении и поднять уровень АЧХ на 3...4 дБ в области средних частот;

область частот - III - 1...1,5 кГц, на диффузоре формируется первый осесимметричный резонанс с одной узловой окружностью (рис. 3.17, а, б), при этом колебания с радиальными узловыми линиями концентрируются на внешнем крае диффузора, а узловая окружность располагается примерно на расстоянии одной трети длины образующей от подвеса. В этой области частот характерно для многих конструкций ГГ появление на АЧХ пика-провала (рис. 3.17 а, б), который обусловливается тем, что первый резонанс осесимметричных колебаний диффузора совпадает со вторым резонансом подвеса, если они оказываются в фазе, на АЧХ появляется пик, в противофазе - провал. Для уменьшения неравномерности АЧХ в этой области частот применяют различные конструктивные и технологические меры: наносятся смазки и пропитки на подвес, выбираются специальные конфигурации подвесов, например тангенциальные, обеспечивающие значительный сдвиг второй резонансной частоты в область высоких частот;

область высоких частот - IV- 1,5 кГц и выше, по мере повышения частоты резонансы с радиальными узловыми линиями все больше смещаются к наружному подвесу, амплитуда их уменьшается и, начиная с частоты примерно 2 кГц, они перестают играть существенную роль. Основное влияние на АЧХ оказывают резонансы с окружными узловыми линиями (рис. 3.18). По мере повышения частоты волновая картина перераспределяется: на резонансных частотах (в воспроизводимом диапазоне обычно оказывается 10-13 резонансных частот диффузора) устанавливается целое число окружных узловых линий; при увеличении частоты их число увеличивается, расстояния между узловыми линиями сокращаются, и, когда оно становится меньше длины звуковой волны на той же частоте, уровень излучения падает. Резонансным частотам с окружными узловыми линиями обычно соответствуют пики-провалы в области средних и высоких частот на АЧХ (см. рис. 3.14) (на них накладываются интерференционные пики-провалы за счет дифракционных процессов на ГГ). Для уменьшения амплитуд на этих частотах применяются различные меры с целью увеличения демпфирования в материале диффузора (пропитки, смазки и т. д.); а также конструктивные меры (выбор формы образующей, распределение толщины и плотности и т. д.). Методы теоретического анализа и разработка программ на ЭВМ для расчета вышеуказанных колебательных процессов в элементах подвижной системы ГГ рассмотрены ниже.

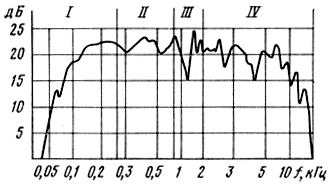
Рис. 3.14. Форма АЧХ широкополосного громкоговорителя

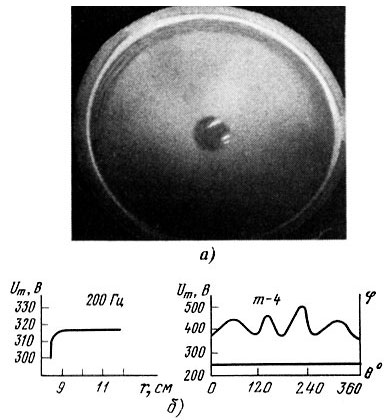
Рис. 3.15. Волновая картина на поверхности диффузора в области низких частот (поршневая область): голографический (а), емкостный метод (б)

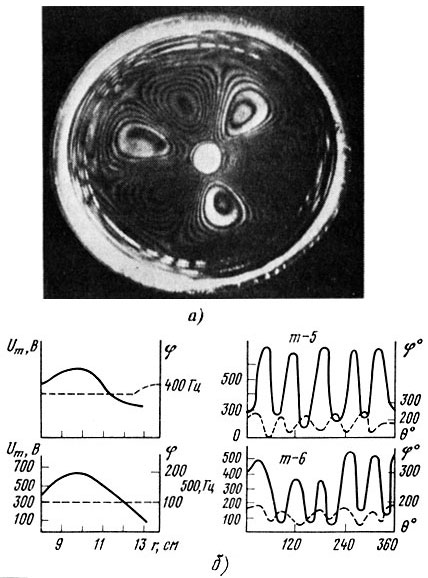
Рис. 3.16. Волновая картина на поверхности диффузора в области средних частот

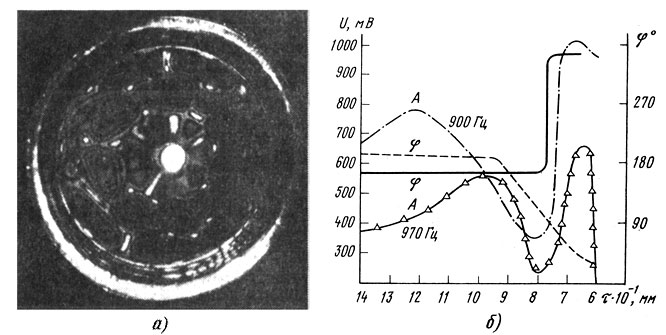
Рис. 3.17. Волновая картина в области первого осесимметричного резонанса

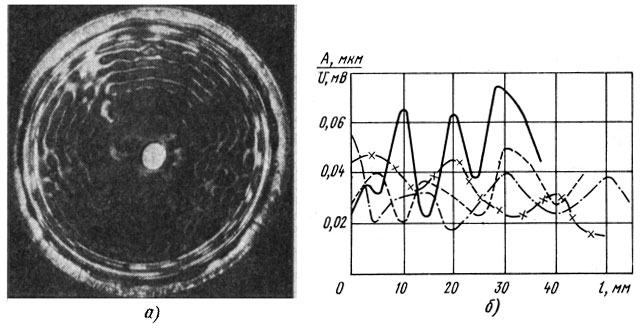
Рис. 3.18. Волновая картина в области высоких частот (а), (б)

Линейные колебательные процессы в гофрированных подвесах и центрирующих шайбах. Как уже было отмечено, основное влияние на излучаемое ГГ звуковое поле, а следовательно, и форму АЧХ и ФЧХ в области низких частот оказывают конструктивные и физико-механические параметры гофрированных подвесов (внешнего подвеса и центрирующей шайбы). Поскольку именно в этой области частот для расчетов ГГ используется метод электромеханических аналогий, очевидно, что параметры ГГ, рассчитанные в § 3.2, в первую очередь зависят от выбора параметров подвесов.

В настоящее время в практике разработок ГГ в основном используются гофрированные подвесы конфигураций, показанных на рис. 3.19. Переход от плоских к гофрированным формам подвесов во всех серийных ГГ был обусловлен стремлением увеличить гибкость с сохранением линейности их упругих характеристик. Поиски различных форм гофрировки подвесов и шайб все время продолжаются, так как к ним предъявляются все более жесткие и противоречивые требования: сохранение линейности упругих характеристик при больших амплитудах смещения (в связи с увеличением подводимой мощности и ростом чувствительности в современных ГГ); увеличение гибкости (снижение упругости) с целью расширения частотного диапазона; повышение динамической устойчивости и др. В первый период создания методов расчета гофрированных подвесов ГГ рассматривался в основном только статистический прогиб, при этом гофрированный элемент заменялся балкой переменного сечения [2, 6]. В связи с тем, что гофрированные элементы приборов широко используются в машиностроении, к настоящему времени теория расчета статических упругих характеристик гофрированных мембран и оценка влияния на них основных конструктивных параметров детально разработаны [49]. Полученные при этом результаты для синусоидальной, тангенциальной и других форм гофрировки могут служить первым приближением для перехода от сосредоточенной гибкости С_{M S} (§ 3.2) к конструктивным параметрам подвесов, поскольку они позволяют оценить степень влияния отдельных элементов (глубины гофрировки, толщины материала, числа и формы гофр) на начальную жесткость и линейность упругих характеристик.

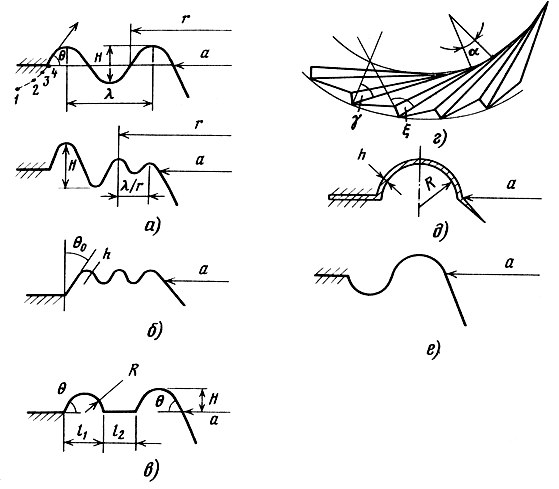
Рис. 3.19. Конфигурации гофрированных подвесов: а - синусоидальные с постоянной гофрировкой; б - с краевым гофром, в - в виде дуг окружностей с плоскими участками, г - тангенциальные; д - тороидальные; е - S-образные

Как следует из графиков, показанных на рис. 3.20, а, наибольшее влияние оказывает глубина гофрировки Н: для мембран с небольшим числом глубоких гофр с увеличением Н начальная жесткость и линейность возрастают; для мембран с мелкой гофрировкой - влияние Н обратное. Значительно влияет на упругие характеристики толщина материала h (рис. 3.20, б). Изменение же числа волн гофрировки n при сохранении глубины Н влияет значительно меньше (рис. 3.20, в), поэтому форма упругой характеристики в основном зависит от H/h. Существенное влияние на статические параметры оказывает наличие краевого гофра, что значительно продлевает линейный участок упругой характеристики. Именно поэтому гофрированные подвесы с краевым гофром (см. рис. 3.19, б) нашли применение в ряде серийных конструкций ГГ. Необходимо отметить также, что существенное влияние оказывает выбор формы краевого гофра (например, гофр цилиндрической формы влияет на упругость характеристики мембраны меньше, чем гофр тороидальной формы).

На упругие характеристики гофрированного элемента оказывает влияние выбор точки закрепления по наружному краю. Наилучшие результаты получаются при закреплении в точке 1 - минимума волны гофрировки (см. рис. 3.19, а), в то же время у большинства ГГ подвес закрепляется в точках 2...4, что обеспечивает при заданном давлении (силе) большую величину прогиба, но меньшую симметричность упругих характеристик. Поскольку подвес соединен на внутреннем крае с диффузором, который на низких частотах можно рассматривать как жесткий поршень, результаты по оценке влияния жесткого центра на статические упругие характеристики гофрированных элементов могут быть использованы при выборе ширины подвеса (обычно ширина подвеса b в серийных массовых ГГ выбирается порядка 2b ≈ (0,09...0,16) D_ГГ).

Однако гофрированные подвесы используются в ГГ в динамических режимах, поэтому наибольшую информацию может дать только количественный анализ их собственных и вынужденных колебаний. В разработках методов расчета этих колебаний можно выделить три направления. К первому относятся [50, 51], где для расчета собственных частот и амплитуд вынужденных колебаний использовался метод замены гофрированного элемента конструктивно-анизотропным плоским кольцом. С помощью этого метода были разработаны методики для расчета первых резонансных частот и амплитуд вынужденных линейных колебаний для подвесов ГГ с различными видами гофрировки: синусоидальной постоянного и переменного сечения, в виде дуг окружностей с плоскими участками, тангенциальной и др. Уравнение свободных гармонических колебаний для анизотропного плоского кольца имеет следующий вид:

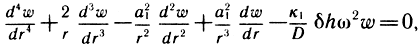
где w - поперечное смещение, r - текущий радиус (см. рис. 3.19, a), D - изгибная жесткость; δh - поверхностная плотность материала подвеса; ω - частота, а² = К₁К₂ - коэффициент анизотропии. Решение этого уравнения с граничными условиями, учитывающими различные варианты закрепления подвесов, вариационным методом Бубнова-Галеркина позволило получить аналитические выражения для расчета резонансных частот и амплитуд вынужденных колебаний. Форма гофрировки на полученные результаты влияет через коэффициенты анизотропии к₁ и к₂(а² = к₁к₂). Последние определяют из условия равенства жесткостей при растяжении и при изгибе анизотропной пластинки и гофрированной мембраны:

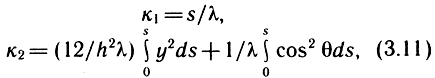
где s - длина дуги одной волны профиля, λ - длина волны, у - расстояние от точки гофра до оси z, h - толщина мембраны, θ - угол между касательной и осью (рис. 3.19, а). Таким образом, коэффициенты к₁ и к₂ зависят от геометрии профиля гофрированного подвеса и его толщины, их аналитические выражения для различного вида гофрировки будут следующие:

для синусоидального профиля с постоянной высотой гофрировки (см. рис. 3.19, а) уравнение профиля гофр: у = H/2sin2πr/λ. Длина дуги

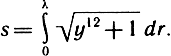
  Коэффициенты анизотропии

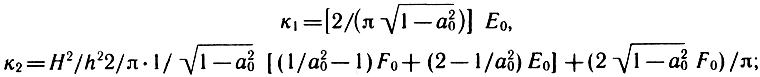
где E₀, F₀ - эллиптические интегралы I и II рода; а₀ = (πH/λ)[1 + (πH/λ)²]^0,5. Если закрепление края подвеса не совпадает со средней линией поверхности, а сдвинуто, например в точку 3 (рис. 3.19, а), уравнение профиля гофр:

где С - сдвиг срединной линии, а к₁ и к₂ определяются по (3.11); для подвеса в виде дуг окружностей с плоскими участками (см. рис. 3.19, в) коэффициенты анизотропии

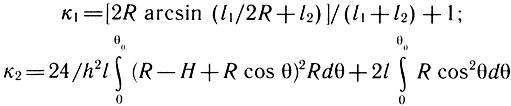
Здесь основными варьируемыми конструктивными параметрами являются Н - высота гофра; l₁, l₂ - соответственно длины хорды дуги и плоского участка; R - радиус окружности образующей дуги профиля; θ - угол наклона касательной.

Аналитические выражения для коэффициентов анизотропии таких сложных геометрических форм, как тангенциальная гофрировка, получены в [51]. Основными конструктивными параметрами, определяющими динамические характеристики подвеса, являются (см. рис. 3.19, г): α - угол, определяющий число граней на подвесе; γ - угол среза внешней грани; ξ - угол наклона боковых поверхностей грани, R и r - внешний и внутренний радиусы, h - толщина.

Если вдоль ширины подвеса меняются высота, длина волны или другие параметры, формулы для расчета резонансных частот и амплитуд несколько усложняются, так как изменяется вид исходных уравнений. Расчет подвесов с переменной синусоидальной гофрировкой и с краевым гофром (рис. 3.19, б) проводится с использованием того же метода. Полученные аналитические выражения для расчета резонансных частот и амплитуд смещения позволили создать методики расчета подвесов геометрических форм, показанных на рис. 3.19 с использованием ЭВМ типа СМ-4. Теперь эти методики применяются в практике разработок ГГ. Расчеты по ним дают возможность количественно оценить влияние параметров гофрировки на резонансные частоты и амплитуды смещения. Например, показанные на рис. 3.21 зависимости первой и второй резонансной частоты f₁ и f₂ от глубины гофрировки H, длины волны λ и толщины h для подвесов с постоянной синусоидальной гофрировкой позволяют установить, что значения первой резонансной частоты f₁ достигают минимума для определенного значения глубины Н и длины волны λ, в то время как вторая резонансная частота f₂ монотонно уменьшается с увеличением H, что дает возможность выбрать с помощью ЭВМ наилучшие сочетания параметров.

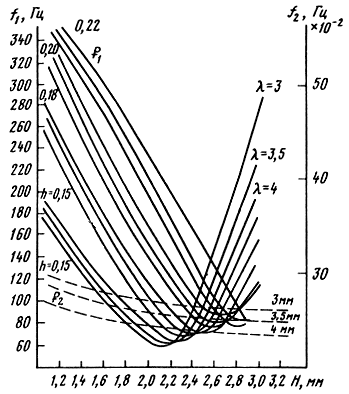
Рис. 3.21. Зависимость первой и второй резонансной частоты от параметров подвеса с постоянной синусоидальной гофрировкой

Расчеты, выполненные для тангенциальных подвесов (рис. 3.22), показывают, что увеличение числа граней вызывает значительное повышение первой и второй резонансной частоты. Существенное влияние на повышение обеих резонансных частот оказывает увеличение угла наклона боковых поверхностей грани ξ и внешнего угла γ. Метод расчета гофрированных подвесов как конструктивно-анизотропных плоских кольцевых пластин позволяет получить с удовлетворительной для практики точностью значения первых резонансных частот и амплитуд смещения прежде всего для подвесов с относительно неглубокой гофрировкой и числом гофр n ≥ 3, а также для гофрировок сложного профиля (типа тангенциальных). Однако для подвесов с глубокой гофрировкой и малым числом гофр точность, полученная вышеуказанным методом, оказывается недостаточной.

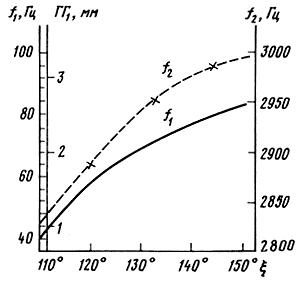
Рис. 3.22. Зависимость первой и второй резонансной частоты от параметров подвеса с тангенциальной гофрировкой

Второе направление в решении динамических задач колебаний подвесов [52] использует более точные исходные уравнения пологих оболочек вращения, решение ищется вариационным методом в виде степенных рядов по специальной системе функций, учитывающих специфику гофрировки. Поскольку такой подход оказался наиболее эффективен при решении нелинейных задач колебаний подвесов, то он более подробно рассмотрен в § 3.7.

И наконец, в настоящее время интенсивно развивается третье направление - применение современных численных методов решения на ЭВМ. В этом случае используется полная система уравнений теории непологих оболочек вращения, решение ищется, например, вариационно-разностным методом, что позволяет рассчитать полный спектр собственных частот и амплитуды вынужденных колебаний во всем воспроизводимом диапазоне. Такой подход является общим для оболочек любой геометрии, поэтому он подробно рассмотрен ниже. Применение его для расчета собственных и вынужденных колебаний тороидальных подвесов [53], широко используемых в низкочастотных ГГ, позволило построить количественные зависимости спектра собственных частот и собственных форм от конструктивных параметров подвеса (рис. 3.23): радиуса кривизны, толщины, ширины и т. д. Результаты расчетов для подвесов ГГ диаметром 200 мм из пропитанной ткани с параметрами E = 6 ⋅ 10⁸ н/м², γ = 0,02; ρ = 0,865 ⋅ 10³ кг/м³ показаны на рис. 3.23, а, б. Аналогичным образом рассчитываются подвесы 5-образной формы и др.

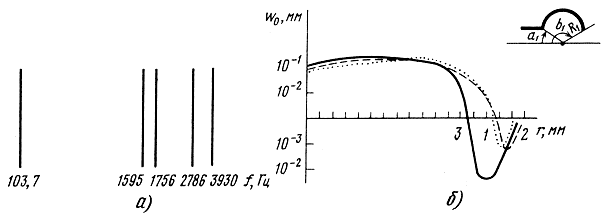
Рис. 3.23. Зависимость спектра (а) и первой формы собственных колебаний (б) от параметров тора: 1 - R₁ = 1,2 см; а₁ = 36°; b₁ = 141°; 2 - R₁ = 0,9 см; а₁ = 28°; b₂ = 150°; 3 - R₁ = 0,6 см; а₁ = 10°; b₂ = 165°

В качестве центрирующих шайб в ГГ также используются гофрированные оболочки. Типичные виды шайб, используемые в серийных конструкциях, показаны на рис. 4.22. Обычно это оболочки с пологой синусоидальной гофрировкой с числом гофр n ∼ 5-6, нередко применяется краевой гофр цилиндрической или тороидальной формы. Для расчета резонансных частот таких конструкций могут быть использованы все вышеперечисленные методы, однако центрирующие шайбы обычно изготавливаются из сетчатых анизотропных материалов (тканей), что значительно усложняет расчет возникающих в них упругих деформаций.

Таким образом, созданные в настоящее время методы расчета и соответствующие комплексы программ на ЭВМ (типа СМ-4, ЕС-1045, БЭСМ-6 и др.) позволяют по заданным конструктивным и физико-механическим параметрам рассчитать спектр собственных частот и амплитуды вынужденных колебаний подвесов различных конфигураций, а также установить влияние изменений этих параметров на резонансные частоты f_i и амплитуды w, т. е. решить задачи анализа. Решение задач синтеза, как было показано выше, точно не реализуется, во-первых, ввиду неоднозначности этой связи, во-вторых, из-за отсутствия решения задач оптимального синтеза для механических распределенных колебательных систем такого типа. Поэтому в практике разработок гофрированных подвесов ГГ обычно используется процедура последовательных приближений: выбирается аналог конструкции (из опыта предшествующих разработок и анализа технической литературы, патентов, каталогов и т. д.), рассчитываются по одной из вышеперечисленных методик его резонансные частоты и амплитуда, сопоставляются с требуемыми значениями f₁ и f₂ и др., полученными из предыдущих расчетов, и затем производится (экспериментально или численно на ЭВМ) направленное изменение конструктивных и физико-механических параметров. Поскольку в настоящее время методы оптимального синтеза механических систем интенсивно развиваются, проводимые работы позволяют ожидать формализации этой процедуры на современных ЭВМ.

Методы расчета стационарных колебательных процессов в диафрагмах. Подвижная система ГГ представляет собой конструкцию, состоящую из нескольких сопряженных оболочек (диффузор, подвес, колпачок, центрирующая шайба, звуковая катушка), каждая из которых имеет свои геометрические (форму образующей, распределение толщины и т. д.) и физико-механические (модуль упругости, плотность, коэффициент затухания) параметры. Модели наиболее типичных конструкций подвижных систем показаны на рис. 3.24. Как было показано выше, в области низких частот определяющее влияние на форму АЧХ имеют параметры гофрированных подвесов, при этом созданные до настоящего времени приближенные методы расчета колебательных процессов в подвесах в основном рассматривали влияние диффузора, шайбы и катушки через сосредоточенную граничную массу и гибкость. В области средних и высоких частот геометрия и свойства материала диффузора начинают вносить основной вклад в излучаемое звуковое поле и поэтому здесь становится необходимым расчет колебательных процессов во всей совокупности сопряженных распределенных оболочек. Решение таких задач представляет значительные математические трудности и стало активно развиваться только в последние годы в связи с совершенствованием численных методов и средств вычислительной техники.

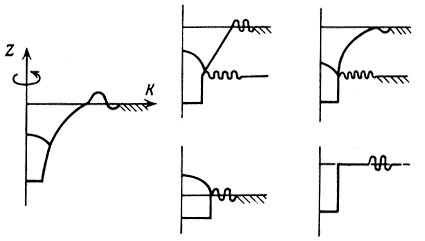
Рис. 3.24. Виды подвижных систем

В 60-е годы на первом этапе исследований громкоговорителей подвижная система рассматривалась как упругая оболочка с прямолинейной или криволинейной формой образующей и упругим закреплением краев (т. е. с учетом граничных масс или граничных гибкостей). При решении задач использовались уравнения теории тонких оболочек вращения, при этом применялся либо метод степенных рядов, либо один из энергетических методов (метод Рэлея или Бубнова-Галеркина). Смещения представлялись в виде ряда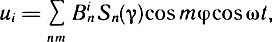  
  где S_n(γ) - аппроксимирующие функции, вид которых определялся формой образующей и граничными условиями. С помощью этих методов были рассчитаны первые собственные частоты и построены их зависимости от основных конструктивных параметров диафрагмы: кривизны, толщины, жесткости и т. д. Интересно отметить, что минимальным значениям собственных частот, рассчитанным для диафрагм различной кривизны, соответствуют волновые конфигурации с большим числом волн по окружности 4-8, что соответствует приведенным выше экспериментальным результатам § 3.4. Например, расчеты, выполненные для ГГ диаметром 150 мм, позволили установить, что низшее значение собственной частоты f₁ = 1086 Гц для диффузора с радиусом кривизны образующей R = 160 мм соответствует n = 1, m = 6, а для диффузора с R = 80 мм n = 1, m = 8 и f₁ = 2838 Гц и т. д. (n - число полуволн по окружности, m - число волн по образующей). Эти данные дают возможность также количественно оценить сдвиг первой резонансной частоты диффузора при увеличении кривизны образующей.

Энергетические методы дают удовлетворительную точность только в области первых собственных частот, с увеличением частоты их точность падает, поэтому в этот же период параллельно с применением энергетических методов начали развиваться численные методы. Последние первоначально использовались для расчета прямолинейных конических диафрагм ГГ при упрощенных граничных условиях с жестким защемлением по внутреннему краю и свободным по наружному. Общие уравнения теории тонких оболочек сводились к системе шести обыкновенных дифференциальных уравнений первого порядка, которая решалась методом Рунге-Кутта. Продолжением этих исследований можно считать [55], где также путем ряда упрощений общие уравнения сводились к системе обыкновенных дифференциальных уравнений восьмого порядка, рассматривались только осесимметричные колебания и применялись аналогичные численные методы. Предложенные методы давали удовлетворительные результаты только для оболочек в основном с короткой прямолинейной образующей, иначе приходилось разбивать оболочку на сегменты, что значительно увеличивало время вычислений и снижало точность.

В этот же период был развит более общий подход к расчету собственных и вынужденных колебаний диафрагм ГГ [56]. Диафрагма рассматривалась как оболочка вращения произвольной формы, физико-механические и геометрические параметры которой менялись вдоль образующей произвольным образом. При этом учитывался широкий класс граничных условий (жесткое защемление, наличие сосредоточенных сил и масс, затухание в материале и т. д.). В качестве расчетной использовалась полная система уравнений, для решения которой применялся вариационно-разностный метод. Был разработан пакет программ на ЭВМ, позволивший рассчитать спектры собственных частот, амплитуды вынужденных колебаний для диафрагм различных конфигураций и оценить влияние на них конструктивных параметров. Таким образом, несмотря на то, что за этот период был достигнут значительный прогресс в изучении процессов колебаний в диафрагмах, все рассмотренные выше численные методы позволяли анализировать только отдельно взятую оболочку (диафрагму), заменяя воздействие на нее остальных элементов подвижной системы через приведенные сосредоточенные параметры.

В настоящее время активно развиваются методы, позволяющие рассчитывать колебательные процессы в подвижных системах, с учетом взаимодействия всех входящих в нее элементов. Наибольшее распространение для этих целей получил метод конечных элементов. Идея метода состоит в разбиении упругого тела на конечное число блоков элементов и упрощении кинематических связей между ними, осуществляемых через узловые точки. Метод конечных элементов представляет собой разновидность вариационных методов и в силу своей универсальности находит широкое применение для решения многих задач механики. С конца 70-х годов японскими исследователями выполнялся комплекс работ по расчету колебательных процессов в подвижных системах ГГ с использованием разработанного в США пакета прикладных программ для структурного анализа сложных конфигураций методом конечных элементов, получивших название Nastran (Network and System translator) [56, 57]. В этом комплексе подвижная система рассматривалась как совокупность оболочек. Была выполнена численная оценка влияния конструктивных параметров подвеса, диффузора, каркаса звуковой катушки, пылезащитного колпачка на спектр собственных частот, амплитуд вынужденных колебаний и амплитудно-частотные характеристики звукового давления. При этом использовались некоторые ограничения: исследовались только осесимметричные колебания, физико-механические параметры считались постоянными, форма диафрагмы выбиралась прямолинейной или близкой к ней; применялась довольно разреженная расчетная сетка (например, на подвес отводилось 10 узлов, на диффузор - 25), что позволяло получить удовлетворительное совпадение с расчетными данными только в области второго - третьего резонанса (2...4 кГц).

Специфика метода состоит в том, что замена реальной оболочки на приближенную, состоящую из набора конечных элементов [58], создает значительную погрешность и требует увеличения их числа, особенно для оболочек таких сложных геометрических форм, как подвес ГГ, а это, в свою очередь, приводит к значительному увеличению времени вычислений. Вероятно, значительное расширение возможностей метода конечных элементов будет связано с внедрением нового поколения ЭВМ с большим быстродействием специально ориентированных на решение задач с его применением.

Для расчетов подвижных систем ГГ в отечественной практике был разработан другой метод и создан пакет прикладных программ [58], позволяющий производить расчет колебательных процессов в оболочках без замены их формы поверхности на приближенную. В качестве математической модели подвижной системы используется сопряженная конструкция (рис. 3.24), состоящая из произвольного числа упругих оболочек вращения, которые могут иметь различные формы образующей (дуга окружности, синусоида, прямая и т. д.). Относительно образующей γ делается только предположение, что она состоит из конечного числа регулярных дуг γ_i, т. е. образующая может быть образована отрезками различных кривых, например парабола + дуга окружности, прямая + синусоида, полусфера + отрезок тора и т. д. Физико-механические параметры (плотность, модуль Юнга, коэффициент демпфирования) могут произвольно меняться вдоль меридиана оболочки, причем в точках стыка различных участков образующей они могут иметь скачки непрерывности. Для границ оболочек, входящих в составную конструкцию, предусмотрен широкий класс граничных условий, позволяющих учесть условия упругого защемления с учетом поглощения в опорах, наличия сосредоточенных масс и внешних сил, условия жесткого защемления и др. Такая модель описывает практически большинство используемых в настоящее время конструкций подвижных систем ГГ (с конусными, купольными диафрагмами, плоскими и выпуклыми пылезащитными колпачками и т. д.). Уравнения колебаний оболочки вращения с учетом внутреннего трения под действием внешней гармонической силы имеет вид

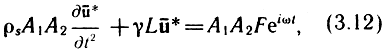
где L - линейный оператор теории тонких оболочек Новожилова, А₁, А₂ - параметры Лэме, описывающие геометрию оболочки;

u^* = (u^*₁, u^*₂, u^*₃) - комплексный вектор смещения, заданный своими проекциями по касательным и нормали к меридиану и параллели оболочки; ρ_s - поверхностная плотность оболочки; F = (F₁, F₂, F₃) - вектор внешней нагрузки; γ - комплексный множитель, учитывающий затухание в материале.

Решение уравнения (3.12) и внешняя нагрузка задаются в виде

где k - число полуволн вдоль параллельной оболочки; φ - угол поворота вокруг оси z. Подстановка (3.13), (3.14) в (3.12) позволяет провести разделение переменных и преобразовать (3.12) к виду

Уравнение (3.15) должно быть дополнено граничными условиями, которые определяются характером закрепления оболочек по линиям сопряжения, а также наличием на них сосредоточенных нагрузок. В общем виде граничные условия представляются следующим образом:

статические условия

где γ_i - комплексный множитель, учитывающий внутреннее затухание в опоре; ν_j - вектор сил и моментов, приложенный по линии сопряжения; К_j - матрица граничной жесткости; R_j - матрица масс; F_j - вектор внешних сил;

геометрические условия сопряжения, учитывающие непрерывность вектора смещения и угла поворота при переходе с одной сопряженной оболочки на другую:

где u^*+ и u^*- - соответственно правый и левый пределы вектора u^* при приближении к линии сопряжения; G_j - матрица, позволяющая учесть скачок непрерывности меридиана на особой линии;

геометрические условия связи, учитывающие наличия жестких защемлений;

где Q_j - матрица перехода от одной системы координат к другой при переходе через линии сопряжения; Е - единичная матрица; Г_j - диагональная матрица, элементы которой равны 0, если смещение и угол поворота вдоль соответствующих координат равны 0.

Для решения задачи используется вариационно-разностный метод, для чего в качестве базисных выбираются кусочно-полиноминальные функции, аппроксимирующие составляющие вектора смещения (u^*₁, u^*₂, u^*₃) на сетке узлов вдоль образующей. Метод позволяет свести решение задачи к решению системы линейных уравнений блочнотрехдиагонального вида

Данная система решается на ЭВМ методом блочной прогонки Гаусса. Созданный комплекс программ, ориентированный на машины типа ЕС-1045, БЭСМ-6, позволяет рассчитывать спектр собственных частот и амплитуды вынужденных колебаний как для каждой отдельной оболочки (подвеса, диффузора), так и всей совокупности входящей в подвижную систему ГГ, а также построить их количественные зависимости от основных параметров оболочек. Например, расчет подвижной системы низкочастотного ГГ диаметром 380 мм с параметрами, показанными в табл. 3.3, позволил определить спектры собственных частот для диффузора, подвеса и совокупности: подвес, диффузор, звуковая катушка (табл. 3.4).

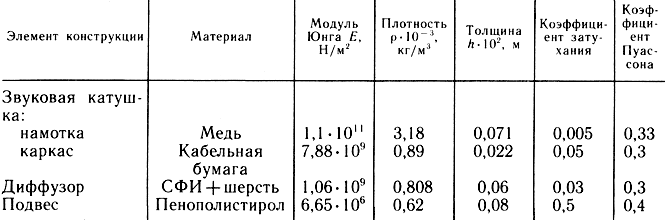
Таблица 3.3

Таблица 3.4

Обобщая результаты расчетов, полученных различными методами, можно количественно оценить влияние конструктивных и физико-механических параметров отдельных элементов подвижных систем (подвесов, ЗК, колпачка и диффузора) на общую структуру колебательных процессов. Результаты расчетов, показанные на рис. 3.25, а, позволяют установить существенное различие в смещениях диафрагмы с колпачком и без него, что соответственно сказывается и на характер изменения звукового давления в области средних частот 2...4 кГц. Влияние параметров звуковой катушки и тороидального подвеса показано на рис. 3.25, б. Смещение спектра собственных частот при изменении угла раскрыва диффузора приведено на рис. 3.25, в.

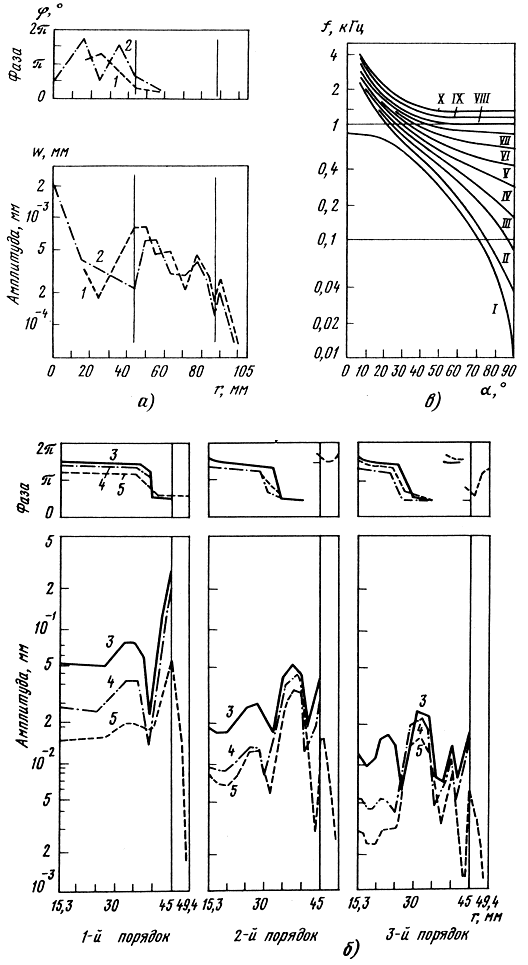
Рис. 3.25. Влияние на амплитуды и фазы смещения колпачка (а), звуковой катушки (б); зависимость спектра собственных частот от угла раскрыва конуса (в): 1 - конус; 2 - конус с колпачком; 3 - конус со свободными краями; 4 - конус со ЗК; 5 - конус со ЗК и подвесом; I-X - номер моды колебаний

Таким образом, создаваемый в настоящее время комплекс программ по расчету собственных и вынужденных колебаний в подвижных системах ГГ различных конфигураций позволяет количественно установить влияние конструктивных и физико-механических параметров, выявить наиболее значимые из них и приступить к решению задач синтеза: по заданным выходным характеристикам ГГ синтезировать на ЭВМ параметры диафрагмы, подвеса, колпачка и др.