
3.5. Акусто-механическое преобразование сигналов в ГГ. Методы расчета звуковых полей
В подсистеме - "излучающая диафрагма + воздушная среда" в электродинамических ГГ осуществляется акусто-механическое преобразование сигнала: механические смещения на поверхности диафрагмы u* (α, β, t) преобразуются в звуковое давление p(R, t). Создаваемая при этом структура звукового поля и излучаемая акустическая мощность определяют объективные параметры и качество звучания ГГ. Полная математическая модель для расчета звукового поля ГГ может быть описана следующим образом (рис. 3.26, а): корпус произвольной формы с поверхностью SK (наиболее распространенным в АС является корпус прямоугольной формы) имеет отверстие радиуса а, в нем установлен ГГ, подвижная система которого образована сопряжением нескольких оболочек различных конфигураций (криволинейный конус, купол, тор и др.). Поверхность корпуса делит пространство на две области: внутреннюю V1 и внешнюю V2. Задача расчета звукового поля для ГГ в оформлении может быть сведена к решению уравнения следующего вида:
Ф± + к2Ф± = 0, (3.20)
где Ф± - потенциал звукового поля, связанный со звуковым давлением соотношением р± = iωρФ±, к = ω/с - волновое число (знак "+" относится к внешней области V2, знак "-" к внутренней V1). Построение решения должно выполняться с учетом граничных условий:
на поверхности диафрагмы SГГ:
∂Ф±/∂n = ±υK, (3.21)
где υГГ - нормальная составляющая колебательной скорости на излучающей поверхности диафрагмы, n - нормаль к поверхности;
на поверхности корпуса SК:
∂ Ф±/∂n = ±υK, (3.22)
и условий излучения Зоммерфельда:
Ф+(R) = 0(1/|R|); ∂Ф+(R)/∂|R| - ikФ+(R) = 0(1/|R|). (3.23)
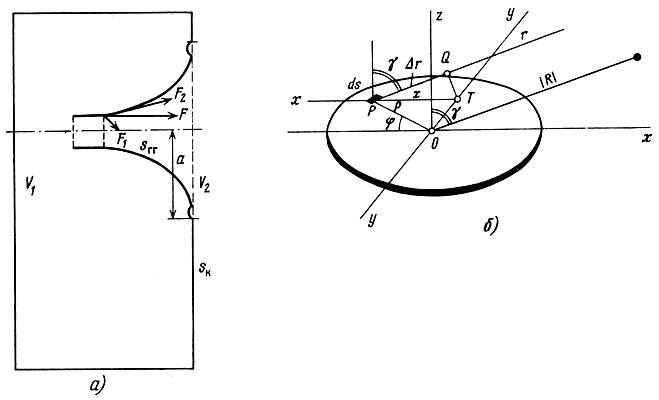
Рис. 3.26. Расчетная модель громкоговорители (а) и поршневого излучателя (б)
Таким образом, задача сводится к решению внешней и внутренней задачи Неймана для трехмерного уравнения Гельмгольца, что дает возможность по известной нормальной компоненте колебательной скорости на поверхности диффузора υГГ и корпуса υK рассчитать распределение потенциала поля (т. е. звукового давления). Полное решение такой задачи представляет значительные математические трудности, обусловленные сложностью формы поверхности SГГ, SK и необходимостью проводить расчет в очень широком диапазоне частот (20...30000 Гц). Кроме того, распределение колебательной скорости на поверхности диффузора и корпуса также должно рассчитываться с учетом влияния на него внутреннего и внешнего звуковых полей, т. е. в общем случае должна решаться сопряженная задача
L3i(u*) = F(t) - (p+ - p-), (3.24)
где L3i - операторы теории оболочек; F(t) - вынуждающая сила (см. § 3.4); р± - звуковые давления, определяемые из решения задачи (3.20)-(3.23). Точное аналитическое решение сопряженных задач (3.20)-(3.24) известно лишь для ограниченного числа поверхностей (круглая пластинка, сфера и т. д.). Для реальных сложных поверхностей диффузоров и корпусов такие задачи начали решаться численными методами на ЭВМ только в последние годы и то с учетом ряда упрощающих предположений. В настоящее время в подавляющем большинстве работ по электроакустике для расчета звукового поля ГГ в оформлении используется приближенная формула:
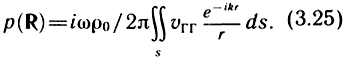
Эта формула, получившая название интеграла Рэлея, дает точный результат, если излучающая поверхность плоская и помещена в бесконечный абсолютно жесткий экран, так как колебательная скорость должна быть задана на бесконечной поверхности s = = sГГ + sэкр. Если колебательная скорость задана на ограниченной части плоскости, например конечный экран, или поверхность изогнута, формула (3.25) дает только приближенные оценки и может использоваться, если поверхность излучения достаточно гладкая, имеет большие размеры по сравнению с длиной звуковой волны и отсутствуют эффекты дифракции волны от отдельных участков, т. е. поле создается только за счет вклада участков s, которые видны из точки наблюдения [59].
Поскольку точный расчет интеграла Рэлея тоже достаточно сложен, на практике пользуются различными приближениями, причем выбор того или иного метода определяется факторами, учитываемыми при расчете: расстоянием от излучающей поверхности (дальнее - ближнее поле), частотным диапазоном (низкие, средние или высокие частоты), формой поверхности (плоский диск, конус, выпуклый или вогнутый купол и т. д.), характером распределения колебательной скорости на поверхности и формой оформления (бесконечный или конечный экран, закрытый ящик и др.). Если исследуется звуковое поле на дальнем расстоянии, т. е. |R| >> 0 (рис. 3.26, б), формула (3.25) упрощается за счет того, что в разложении в ряд показателя при экспоненте остаются только линейные члены:
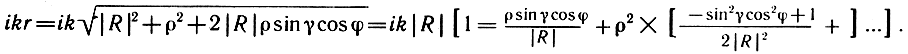
В этом случае (3.25) приводится к виду
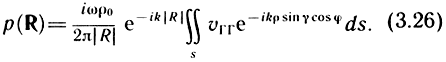
Это упрощение называется приближением Фраунгофера, условие его применения ka2/|R| << 1 (а - радиус излучателя, k = ω/с - волновое число). Если круглый плоский поршень помещен в бесконечном экране в дальнем поле в приближении Фраунгофера получается еще более простая формула для расчета звукового давления на оси:
|p| = (ωρ0sυ0/2πR)[2J1(kasinγ)/kasinγ],
где J1(kasinγ) - функция Бесселя 1-го порядка; |R| - расстояние до точки наблюдения; γ - угол между осью и направлением на точку наблюдения. Полученная формула используется в большинстве работ по расчету АЧХ ГГ, несмотря на то, что возможности ее применения для реальных ГГ ограничены. Когда условие ka2/|R| << 1 не выполняется, например на малом расстоянии, то звуковое давление рассчитывается в приближении Френеля, т. е. в разложении (3.26) должны сохраняться и квадратичные члены. Если построить график зависимости звукового давления от расстояния на оси круглого поршневого излучателя в экране (рис. 3.27, а), то в дальнем поле, где ka2|R| << 1, оно спадает по закону 1/R (зона Фраунгофера), на более близком расстоянии оно имеет интерференционные максимумы и минимумы (зона Френеля). Наконец, вблизи или на поверхности излучателя для расчета звукового давления необходимо точно вычислить интеграл Рэлея. Для этого используются методы разложения его в ряды, асимптотические и численные методы [60] (например, метод Симпсона).
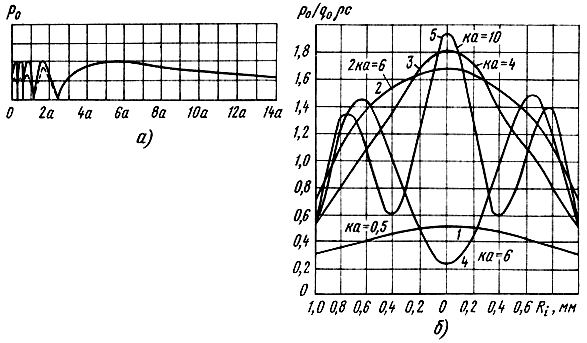
Рис. 3.27. Распределение звукового давления на различных расстояниях от диафрагмы на оси (а) и на поверхности (б)
Применение численных методов позволяет производить расчет звукового давления на любых расстояниях и для любых плоских форм излучателей (круглые, прямоугольные, кольцевые и т. д.). Расчет давления на поверхности излучателя необходим для приближенной оценки влияния среды на распределение колебательной скорости на поверхности, что обычно делается с помощью учета активной и реактивной составляющих импеданса излучения.
Распределение давления на поверхности круглой поршневой диафрагмы на разных частотах показано на рис. 3.27, б. Расчеты импеданса для излучателей разных форм выполнены в [45]. Расчет звукового поля с помощью интеграла Рэлея может быть выполнен и для случая неоднородного распределения скорости на поверхности излучателя. Для этого закон распределения скорости должен быть задан аналитически или численно. И наконец, интеграл Рэлея используется для приближенного расчета звукового поля от неплоских излучателей, помещенных в бесконечный жесткий экран. Так, звуковое поле поршневого конусного излучателя в бесконечном экране (рис. 3.28), рассчитывается по формуле
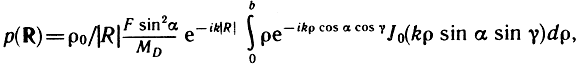
где F - вынуждающая сила; MD - масса подвижной системы, остальные обозначения показаны на рис. 3.28, а. Расчеты, выполненные по этой формуле, показывают, что в области низких частот характер изменения звукового давления акустической мощности и характеристики направленности для жесткого поршня и конуса в бесконечном экране практически совпадают. Начиная с частоты fc = (ctgα)/πRB, звуковое давление на оси конуса падает (рис. 3.28, б), характеристика направленности у жесткого конуса становится существенно шире, чем у плоского поршня (рис. 3.28, в).
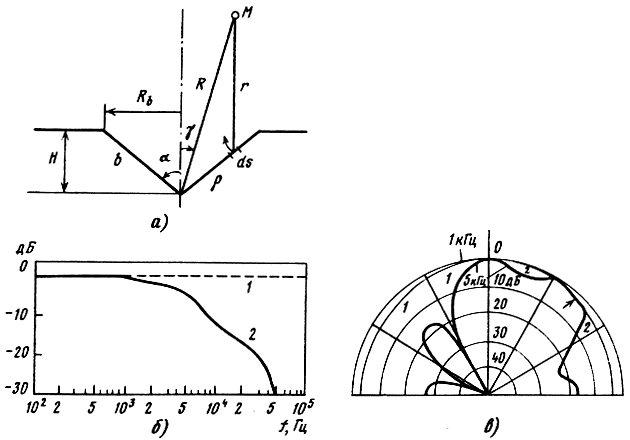
Рис. 3.28. Расчетная схема конического излучателя (а); зависимость звукового давления от частоты (б) и диаграммы направленности для плоского и конического поршня в бесконечном экране (в): 1 - поршень, 2 - конус
Исследования звукового поля конусного излучателя без экрана, а также в экранах конечных размеров выполнены в [61, 62]. Однако, несмотря на широкое применение интеграла Рэлея, в решении различных задач вышеперечисленные ограничения, при которых (3.25) может применяться, не дают возможности производить достаточно точные расчеты звуковых полей излучателей сложных форм в корпусах конечных размеров. Такие задачи решаются с помощью численных методов.
Для разработки численных методов расчетов звуковых полей реальных конусных и купольных громкоговорителей в различных оформлениях необходимо разбить излучаемый диапазон на несколько частотных областей и в каждой из них использовать свои физические и математические модели для анализа процессов излучения:
область низких частот (L >> λ, L - размеры ГГ в оформлении, λ - длина звуковой волны) - для приближенного расчета звукового поля ГГ в корпусе используются различные модели, например поршень в замкнутой сфере или эллипсоиде [61], для этого случая решение построено в аналитической форме. Для точного расчета звукового поля от ГГ в прямоугольном оформлении в настоящее время используются численные методы на ЭВМ (обычно на основе МКЭ) [62]. Однако задача (3.20)-(3.23) может быть сведена к интегральному уравнению следующего вида:
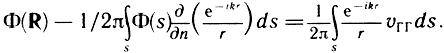
Для его решения используется метод граничных элементов (МГЭ). Разработанный на базе МГЭ комплекс программ на ЭВМ БЭСМ-6, ЕС-1045 позволяет рассчитывать излучение и дифракцию в любой точке поля для излучателей в прямоугольном оформлении (или любом другом) с учетом произвольных законов распределения колебательной скорости на поверхности. Рассчитанная структура звукового поля для излучателя в прямоугольном оформлении, а также влияние глубины и угла раскрыва конуса показаны на рис. 3.29, а и б. Сравнение значений звукового давления для ГГ в закрытом оформлении, рассчитанного точными численными методами и с помощью формулы Рэлея (вычисленной по методу Симпсона на ЭВМ), показывает, что погрешность расчетов по (3.28) в области частот 20...70 Гц составляет в среднем 25% на расстоянии 0,5 м и 19% на расстоянии 1 м для ГГ диаметром 315 мм в прямоугольном корпусе с габаритными размерами 1000 × 500 × 500 мм;
область средних частот (L порядка λ) - для расчета звукового давления также можно применять численные методы, как и в области низких частот. Однако по мере повышения частоты решение задачи (3.20)-(3.23) требует больших затрат машинного времени, поэтому здесь для расчета дифракционных эффектов целесообразно использовать методы лучевой акустики;
область высоких частот (L >> λ) - для расчета можно использовать в качестве модели реального ГГ в следующем оформлении: излучатель в бесконечном экране. Применение формулы Рэлея для такой модели с учетом формы поверхности и сложного закона распределения колебательной скорости на ней позволяет получать достаточно точные результаты [63]. Например, рассчитанное значение звукового давления для купольного излучателя (рис. 3.29, в) позволяет оценить влияние кривизны купола на осевое давление (существенное влияние начинает сказываться с ка = 1, где к - волновое число, а - радиус купола).
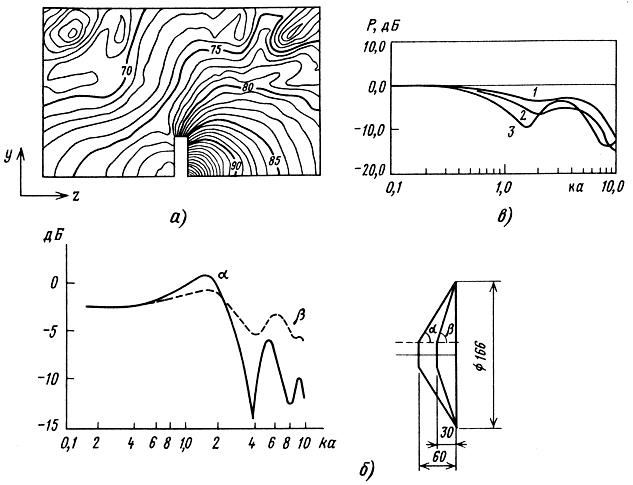
Рис. 3.29. Структура звукового поля вокруг прямоугольного оформления (а); влияние глубины и угла раскрыва конуса (б), влияние кривизны купола (в): 1 - H/а = 0,5; 2 - Н/а = 0,75; 3 - Н/а = 1,0
Для вогнутых излучателей используется метод сшивания решений: внутри области - численные методы, во внешней - расчет интеграла Рэлея.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
