3.6. Нестационарные (переходные) колебательные процессы в электродинамических ГГ

Наряду с исследованием и разработкой методов расчета стационарных колебательных процессов в ГГ, на протяжении всего периода их выпуска проводились исследования нестационарных переходных процессов, поскольку они оказывают существенное влияние на восприятие тембра музыкальных и речевых сигналов. В акустических системах электродинамический ГГ является основным источником переходных искажений, в первую очередь за счет относительно большой массы и сравнительно малого уровня демпфирования в материалах подвижной системы. Исследования переходных процессов в ГГ проводились по следующим направлениям: разработка методов и создание нестандартной аппаратуры для измерения параметров переходных процессов (см. гл. 2), изучение связи параметров переходного процесса с формой АЧХ и конструктивными параметрами диафрагмы, установление порогов слышимости основных параметров переходного процесса и разработка методов их расчета.

Результаты анализа переходных процессов, возникающих в ГГ различных конструкций [64], позволяют выявить в них следующие характерные особенности:

В области низких частот форма переходного процесса определяется значением основной резонансной частоты f_s и добротности Q_T. При возбуждении ГГ пакетами синусоидальных колебаний с частотой заполнения f_s на осциллограммах отчетливо видны процессы экспоненциального нарастания и спада колебаний (см. рис. 2.5, б). Так как параметры переходного процесса - декремент затухания Δ и время спада τ - связаны с добротностью ГГ соотношением Δ = π/Q_T, все конструктивные и технологические меры, направленные на снижение добротности (увеличение электромагнитного и механического демпфирования, уменьшение массы, увеличение гибкости ГГ, подбор параметров оформления и т. д.), приводят к снижению уровня и времени переходного процесса. Измерения параметров различных серийных электродинамических ГГ с бумажными диффузорами показали, что в области частот 30...150 Гц время затухания 0,6...0,7 с. Влияние первого резонанса сказывается и на ближайших к нему частотах. При этом в момент выключения сигнала скачком происходит переход от колебания с вынужденной частотой f_в к колебаниям с собственной частотой f_s. На рис. 3.30 показана осциллограмма затухающих колебаний с частотой f_в = 110 Гц при частоте вынужденных колебаний f_в = 200 Гц. В области средних частот на характер переходного процесса начинает влиять первая резонансная частота диафрагмы (для диффузоров средних размеров диаметром 150...200 мм она обычно находится в области 1000...1200 Гц). Так, для ГГ диаметром 160 мм спад переходного процесса с собственной частотой 1000 Гц начинается примерно с частоты 800 Гц. Непосредственно на резонансной частоте, совпадающей с пиком АЧХ, переходной процесс имеет экспоненциальный характер, на провалах АЧХ на характер переходного процесса оказывают влияние два соседних пика (резонанса) и он носит характер биений (см. рис. 2.5, б), причем на участках спада АЧХ время затухания переходного процесса резко возрастает. В области высоких частот связь характера переходного процесса с формой АЧХ сохраняется: экспоненциальный спад на пиках, биения - на провалах АЧХ. При этом на резонансах подвижной системы, выраженных в виде пиков-провалов АЧХ, уровень и длительность переходных процессов достигают максимальных значений.

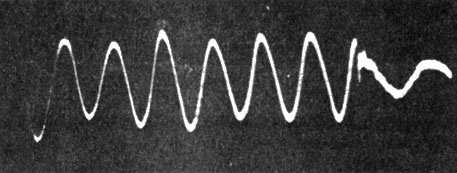
Рис. 3.30. Осциллограмма колебаний переходного процесса на частоте 200 Гц

Анализ параметров переходного процесса для ГГ различных конфигураций и материалов диафрагм позволил построить некоторые усредненные кривые зависимости времени затухания τ от частоты (рис. 3.31, а), а также частотную зависимость уровня среднего давления в паузе (рис. 3.31, б). Сравнение частотной зависимости времени затухания переходного процесса τ с субъективно установленными пороговыми значениями τ_п слышимости процессов установления и спада переходного процесса, определению которых был посвящен большой комплекс работ, показывает, что в области частот до 1000 Гц у большинства ГГ время установления и спада ГГ выше пороговых значений τ_п ≈ 1 мс, в области высоких частот время τ приближается к пороговым τ_п ≈ 0,5 мс. Следует отметить, что чувствительность слуха к переходным процессам в форме затухающих биений существенно повышается, поэтому снижение уровня такого типа переходных процессов является чрезвычайно важным при разработке ГГ.

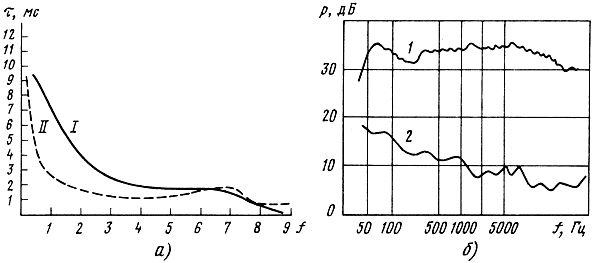
Рис. 3.31. Зависимости времени затухания τ для различных ГГ (I, II) (а) и Р_ср в паузе (б) от частоты: 1 - АЧХ стационарного сигнала; 2 - АЧХ переходного процесса

Как показывают результаты измерений, с увеличением частоты декремент Δ также уменьшается и приближается к значению, определяемому внутренним трением в материале подвижной системы.

Наряду с экспериментальными исследованиями, разрабатываются численные методы анализа переходных процессов. Для расчета в области нижних частот применяется метод электромеханических аналогий, во всем воспроизводимом диапазоне используется методика расчета собственных и вынужденных колебаний диафрагм на ЭВМ, изложенная в § 3.4. Отличия заключаются в том, что в системе уравнений (3.12) правая часть полагается равной 0, а граничные условия дополняются неоднородными начальными условиями:

где u^*(α)ехр(jωt) - решение задачи установившихся вынужденных колебаний под действием синусоидальной нагрузки. Разработанные программы позволяют рассчитать форму переходного процесса в паузе по смещению и по звуковому давлению, а также зависимость формы переходного процесса от конструктивных и физико-механических параметров диафрагм. Результаты экспериментального и теоретического анализа переходных искажений показывают, что наиболее эффективным средством снижения уровня переходных процессов в области средних и высоких частот является увеличение демпфирования в диффузорах (вибропоглощающие покрытия, пропитки, смазки, специальные материалы) и жесткости (выбор формы образующей, распределение толщины и плотности, применение материалов с высоким отношением E/ρ, где Е - модуль Юнга, ρ - плотность). Заметим, что подавляющее большинство фирм переходит в настоящее время на новые методы анализа переходных искажений в ГГ с помощью "кумулятивных спектров" (см. гл. 2). В связи с этим актуальной становится задача поиска новых критериев их оценки (числа и длительности "задержанных" резонансов, их расположения на частотной и временной осях и т. д.).