3.7. Нелинейные колебательные процессы в подвижных системах электродинамических громкоговорителей. Физические модели. Методы расчета

Как уже было показано в гл. 2, в процессе электромеханического преобразования сигналов в электродинамических ГГ возникают различные виды нелинейных искажений, которые могут оцениваться как в частотной, так и во временной областях. Физические процессы, обусловливающие эти нелинейные искажения, могут быть классифицированы следующим образом: нелинейные упругие колебания элементов подвижной системы - подвесов, шайб, диффузоров, колпачков; колебательные процессы при наличии механических дефектов в ГГ, воспринимаемые как дребезжание или призвуки; параметрические колебания диффузоров; частотная модуляция излучаемого сигнала за счет эффектов Доплера, нелинейные электромеханические преобразования в узле "звуковая катушка + магнитная цепь". Рассмотрим эти процессы и методы их расчета более подробно.

Нелинейные упругие колебания элементов подвижной системы ГГ - подвесов, шайб, диффузоров. Экспериментальные исследования гармонических искажений в серийных громкоговорителях показывают, что наибольших значений они достигают в низкочастотной части воспроизводимого ГГ диапазона, где амплитуды смещения подвижной системы особенно велики (рис. 3.32). Нелинейные искажения в области низких частот, где колебания диффузора носят поршневой характер, определяются в основном нелинейностями характеристик подвесов (гофрированного подвеса и центрирующей шайбы) и электромагнитного преобразования в узле "звуковая катушка + магнитная цепь".

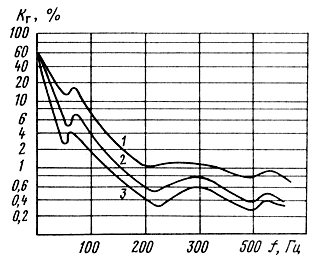
Рис. 3.32. Зависимость К_Г от частоты и величины подводимого напряжения, 1 - U = 4 В; 2 - U = 2 В; 3 - U = 0,63 В

Влияние магнитного поля на нелинейные искажения будет рассмотрено в § 3.8. Как следует из общей теории, характер нелинейного колебательного процесса в упругой системе определяется соответственно ее нелинейной упругостью, нелинейной инерционностью и нелинейным затуханием. Поведение системы в области резонанса зависит от соотношения этих факторов. Резонансная частота, зависящая в нелинейных системах от амплитуды, в случае преобладания нелинейной упругости с ростом амплитуды будет возрастать. При преобладании нелинейной инерционности соотношение будет обратным. Резонансная амплитудная кривая ("явление затягивания") будет наклонена вершиной в сторону больших частот при преобладании нелинейной упругости и в сторону меньших при инерционности и т. д. Эксперименты по исследованию характера резонансных амплитудных кривых в области низких частот позволили установить, что основным определяющим фактором в ГГ является нелинейная упругость.

Исследованию нелинейных искажений в ГГ в области низких частот уделялось в технической литературе достаточное внимание, однако во всех работах подвижная система ГГ заменялась системой с сосредоточенными параметрами, но так как не были установлены зависимости между этими параметрами и конструктивными и физико-механическими параметрами подвесов, то анализ не позволял производить практических расчетов.

Выполненный за последние годы большой объем экспериментальных и теоретических исследований [65] позволил разработать метод и создать пакет прикладных программ для ЭВМ по расчету нелинейных искажений ГГ в области низких частот, обусловленных упругими характеристиками подвесов. Для расчета упругих характеристик подвижной системы в области низких частот была принята расчетная модель, показанная на рис. 3.33. Диффузор рассматривается как система, состоящая из трех оболочек: непологой гофрированной синусоидальной оболочки 1 (такого типа подвесы часто используются для массовых типов ГГ); пологой прямолинейной конической оболочки 2 (в области низких частот, где длина волны велика по сравнению с размерами ГГ, такая модель оправдана для любых форм диффузоров); плоского участка 3 (представляющего пылезащитный колпачок) и упругого основания 4 (параметры которого определяются из экспериментальных измерений упругих характеристик центрирующих шайб). Профиль синусоидального неполого гофрированного подвеса достаточно точно описывается уравнением (см. рис. 3.19):

где τ = ω₁ρ - τ₀; ω₁ = 2πRδ₁/l - π; ρ = r/R; δ₁ = r₁/R.

Деформированное состояние оболочки может описываться двумя функциями: υ(ρ) - угол поворота касательной к поверхности; ψ(ρ) - функция напряжения (ψ) = (-1/EhR)∫T₂dr, где Т₂ - внутреннее нормальное усилие). Для нахождения этих функций используется система дифференциальных уравнений второго порядка:

для непологой гофрированной оболочки (1):

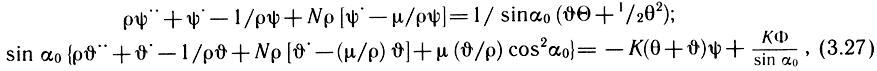
где h - толщина, μ - коэффициент Пуассона; θ = ctg α₀ = F_θsinτ; F_θ = ω₁H/R; N = -ω₁F²_θsin2τ/2(1 + θ²); K = 12(1 - μ²)R²/h²;

для пологой конической оболочки (2):

для круглой плоской пластины (колпачка) (3):

где Ф, Ф_к, Ф_п есть функция сил инерции q, приложенной к диффузору силы Q_c и упругой силы реакции, создаваемой шайбой Q_ш. Задавая закон изменения угла поворота υ в виде υ = - f⋅3ρ(1 - ρ)², учитывая граничные условия сопряжения оболочек (равенство нормальных усилий и радиальных смещений в точках сопряжения), проводится интегрирование уравнений (3.27), (3.28), (3.29) методом Бубнова-Галеркина, что дает возможность построить упругую характеристику подвижной системы:

где B_i = C_i + S_i (i = 1, 2, 3), C_i - коэффициенты, определяемые конструктивными и физико-механическими параметрами гофрированного подвеса, диффузора и колпачка; S_i - коэффициенты упругих характеристик центрирующих шайб, которые определяются из экспериментальных данных, w - смещение центра системы. Полученные данные измерения прогибов центрирующих шайб, серийно выпускаемых ГГ, и их статистическая обработка позволили разработать программу на ЭВМ для полиноминальной аппроксимации результатов измерений методом наименьших квадратов с использованием ортогональных полиномов Чебышева. Результаты измерений и аппроксимации упругих характеристик с учетом разбросов центрирующих шайб для громкоговорителей диаметром 160 показаны на рис. 3.34. Значения коэффициентов аппроксимирующих полиномов и границ интервалов в данном случае имеют вид:

Анализ влияния нелинейности упругих характеристик шайб на общие упругие характеристики подвижной системы показывает, что в целом нелинейность шайбы выше нелинейности подвеса, особенно при малых уровнях подводимого напряжения. В частности, расчеты по (3.30) установили, что кубические члены в упругих характеристиках подвижной системы в основном определяются упругостью центрирующих шайб. Результаты этих расчетов дали возможность определить количественную связь коэффициентов B_i с параметрами подвижной системы. Так, при уменьшении толщины h подвеса начальная жесткость В₁ уменьшается, а нелинейность В₂, В₃ возрастает; при увеличении глубины гофрировки подвеса Н начальная жесткость уменьшается, но кубические члены в (3.30) могут и не снижаться, поэтому увеличение Н без изменения других параметров может не привести к снижению нелинейных искажений.

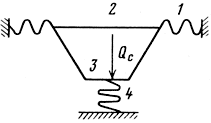
Рис. 3.33. Расчетная модель подвижной системы ГГ в области низких частот

Разработанный метод расчета упругих характеристик подвижных систем позволил перейти к расчету вынужденных нелинейных колебаний подвижной системы ГГ в области низких частот. Дифференциальное уравнение вынужденных низкочастотных колебаний подвижной системы имеет вид

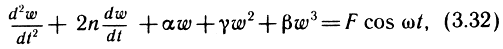
где w - смещение центра системы; α, γ, β - приведенные коэффициенты упругой характеристики (3.30) подвижной системы; F - вынуждающая сила;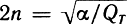  
- коэффициент затухания; Q_T - добротность. С помощью метода гармонического баланса решение (3.32) может быть построено в виде

где A₁, A₂, А₃ и χ₁, χ₂, χ₃ - соответственно амплитуды и фазы первой - третьей гармоник, являющиеся функциями конструктивных и физико-механических параметров подвижной системы.

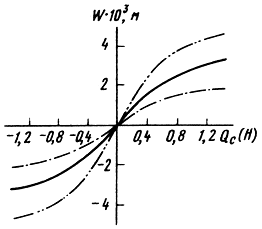
Рис. 3.34. Упругие характеристики центрирующих шайб

Расчет амплитудно-частотных и фазочастотных характеристик, выполненный с помощью специально разработанного пакета прикладных программ на ЭВМ, позволил оценить влияние на них добротности ГГ, упругости центрирующей шайбы, параметров гофрированного подвеса и др. Результаты расчетов, представленные на рис. 3.35 для ГГ диаметром 160 мм, показывают, что вид амплитудно-частотных кривых зависит от добротности системы. При больших добротностях (Q_T > 3) может иметь место явление "скачка" - резкое изменение амплитуды вблизи вершины амплитудной кривой (наличие "скачка" на резонансе ГГ при больших амплитудах было ранее обнаружено экспериментально). При уменьшении добротности Q_T < 2 явление "скачка" практически не наблюдается. Существенное влияние на вид амплитудных кривых оказывает начальная жесткость центрирующей шайбы. С увеличением начальной жесткости разонансная частота увеличивается, а ход амплитудных кривых первой гармоники существенно линеаризуется, однако при этом может иметь место увеличение амплитуд третьей гармоники. Максимумы амплитуд второй и третьей гармоник располагаются соответственно в области f_s/2 и f_s/3 (f_s - резонансная частота системы), что совпадает с экспериментальными данными. Таким образом, пользуясь разработанным пакетом программ, можно в каждой конкретной конструкции ГГ подобрать параметры таким образом, чтобы минимизировать амплитуды вторых и третьих гармоник и линеаризовать характер изменения амплитуд первых. По расчетным значениям амплитудных характеристик были рассчитаны значения коэффициентов гармоник К_Г2 и К_Г3. Расчеты позволили установить влияние на К_Г2 и К_Г3 добротности, толщины, коэффициентов упругости, начальной жесткости шайбы. Влияние добротности показано в табл. 3.5.

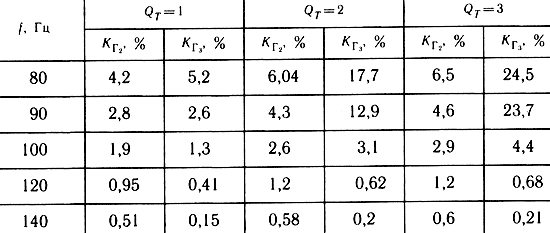
Таблица 3.5

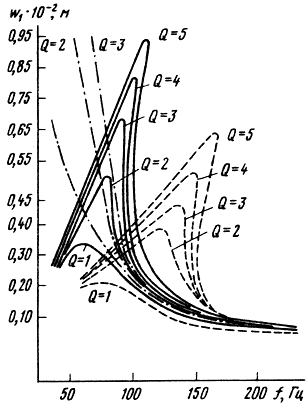
Рис. 3.35. Вид нелинейных амплитудно-частотных характеристик при разных значениях добротности

Как следует из данных таблицы, уменьшение добротности существенно снижает коэффициент гармонических искажений. Так, изменение от Q_T = 3 до Q_T = 1 приводит к изменению К_Г2 от 6,5 до 4,2%, а К_Г3 от 24,5 до 5,2%. Значительное влияние оказывает и начальная жесткость шайбы (переход от шайб с максимальной для данного типа ГГ жесткости к минимальной увеличивает К_Г почти в 2 раза). Нелинейные колебания подвижной системы в области низких частот приводят к появлению в спектре излучаемого сигнала, помимо гармонических, интермодуляционных и разностных искажений, которые порождаются теми же физическими причинами - нелинейностью упругих характеристик подвесов и диффузоров. Для расчета таких искажений в области низких частот используются те же методы [65], что и для расчета гармонических искажений; при этом правая часть уравнения (3.32) принимает следующий вид: F₁cosw₁t + F₂cosw₂t. Расчеты частотно-разностных искажений оказывают, что наибольшее значение имеют амплитуды с частотами f₂ ± f₁. Это определяется в основном квадратичным характером упругих характеристик подвесов.

Существенное влияние на уровень частотно-разностных искажений в области низких частот также оказывает изменение добротности. Так, изменение добротности от 4 до 1 приводит к снижению амплитуд в 1,5...2 раза на частотах 125 и 180 Гц. Заметим, что представленная расчетная модель применима в области, где колебания диффузора носят поршневой характер. В области частот, где находится спектр собственных частот диффузора, необходимо рассматривать задачу о нелинейных колебаниях тонких упругих оболочек вращения отрицательной гауссовской кривизны. Разработка программ для их расчета является в настоящее время актуальной задачей. Опыт разработки ГГ показывает, что все меры, направленные на повышение конструктивной жесткости диффузоров (увеличение кривизны, наличие ребер жесткости и т. д.), а также применение материалов или большой жесткости (E/ρ) или с большим коэффициентом демпфирования (γ) приводят к снижению уровня нелинейных гармонических искажений второго - третьего порядка, обусловленных нелинейными упругими характеристиками диффузоров.

Нелинейные колебания, определяющие дребезжание и призвуки в ГГ. Как было отмечено в гл. 2, в динамических ГГ существует особый вид нелинейных искажений, субъективно воспринимаемых как дребезжание и призвуки. Изучению этих процессов в ГГ уделялось большое внимание в [29, 30]. Характерный звук дребезжания и призвука выявляется чаще всего при возбуждении ГГ в области частоты его резонанса или в более широкой области низких частот вплоть до 2...3 кГц. Анализ особенностей спектров излучения таких ГГ показывает, что нелинейные искажения, возникающие в них, можно разбить на четыре вида (см. рис. 2.10): гармонические низших порядков с n от 2 до 4; гармонические с n от 4 до 10...12, определяющие появление призвуков, и гармонические с n от 10 и выше, воспринимаемые как дребезжание. Кроме того, в спектре могут присутствовать и субгармонические составляющие с частотами 1/2n или 1/3n, вызванные параметрическими колебаниями элементов подвижной системы.

Результаты теоретических и экспериментальных исследований, выполненные за последние годы, показали, что наибольшую информацию для дифференциальной оценки различных видов механических дефектов в ГГ, вызывающих дребезжание и призвуки, дает анализ временной структуры сигнала, излучаемого громкоговорителем в ближнем поле. Статистический анализ осциллограмм излучаемых сигналов серийных ГГ, в которых субъективно диагностировались дребезжание или призвуки, позволил выявить четкую корреляцию различных видов механических дефектов в ГГ с формой, амплитудой, полярностью и месторасположением импульсов дребезжания по отношению к основному моногармоническому сигналу возбуждения. Нелинейные искажения, воспринимаемые в виде дребезжания или призвуков, обусловливаются в ГГ разбросами физико-механических параметров используемых материалов; несоблюдением технологических режимов (процессов размола, отлива, прессования, сборки и др.); нарушением технологии сборки; механическими дефектами, возникающими при транспортировании и хранении ГГ, и т. д. Нарушение технологических режимов в серийном производстве вызывает такие дефекты, как трение катушки в зазоре магнитной цепи, касание выводов диффузора, удар подвижной системы о магнитную цепь, наличие металлической стружки в зазоре, неравномерность структуры диффузора, отклейка шайбы, диффузора, катушки и т. д. Большая часть перечисленных причин (порядка 80%) может рассматриваться как комбинация трех основных явлений: упругий и неупругий удар подвижной системы о жесткий упор; сухое трение при перемещении звуковой катушки в магнитной цепи; колебания и касания выводов о диффузор.

Ударное дребезжание возникает при ударе катушки или диффузора о жесткий упор (например, магнитную систему). При этом может различаться упругий удар, когда подвижная система (ПС) отскакивает от магнитной цепи по определенному закону, зависящему от физико-механических свойств соударяющихся поверхностей, частоты возбуждения и др. Обычно это явление происходит в области резонанса, где подвижная система смещается с максимальной амплитудой. Удар может быть также и неупругим. В этом случае происходит практически остановка подвижной системы, что приводит к появлению отсечки по смещению. В момент удара возникает ударный импульс звукового давления, находящийся в фазе с основным сигналом. В реальных громкоговорителях в момент удара звуковое давление не падает до нуля, так как и при остановке катушки ПС за счет сил инерции продолжает смещаться, возникают переходные процессы, хотя они выражены слабее, чем ударные импульсы.

Временные диаграммы смещения и звукового давления при упругом ударе показаны на рис. 3.36. Структура импульсов дребезжания (полярность, амплитуда, крутизна нарастания фронта, длительность и характер переходного процесса) зависит от величины смещения, колебательной скорости, формы АЧХ, верхней граничной частоты, амплитуды возбуждающего сигнала и т. д. Диагностической характеристикой ударного дребезжания является полярность и амплитуда импульса в начальной стадии его формирования по отношению к сигналу возбуждения.

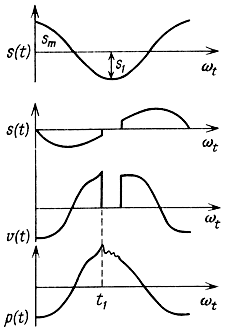
Рис. 3.36. Временные диаграммы смещения, скорости и звукового давления при упругом ударе

При упругом и неупругом ударах, происходящих при смещении подвижной системы, импульсы дребезжания периодически возникают на вершинах положительных (отрицательных) полуволн гармонического сигнала. Полярность импульсов совпадает с полярностью полуволн гармонического сигнала.

Дребезжание из-за трения возникает обычно при попадании металлической стружки в зазор магнитной системы ГГ и при перекосе катушки в зазоре. В обоих случаях происходит затирание (за счет сухого трения) катушки, которое приводит к возникновению дребезжания. Затирание катушки может быть сплошным, если трение непрерывно, или частичным, если трение происходит только в некоторой части перемещения катушки. Процесс формирования сигнала в ГГ при наличии сухого трения будет существенно отличаться от рассмотренного при ударе. Экспериментальные исследования показали, что положение импульса звукового давления дребезжания соответствует моменту равенства нулю колебательной скорости, потому он возникает на максимуме полуволны синусоидального сигнала звукового давления, но с противоположной полярностью. Общий вид сигнала искажения в данном случае показан на рис. 3.37. В момент начала действия трения T₁, приходящегося на область максимальных смещений диффузора (рис. 3.37), возникает дополнительная реакция F′₂ за счет силы сухого трения скольжения. В точке t₂ происходит остановка подвижной системы. В этот момент силы, действующие на подвижную систему, уравновешиваются F′₂ = F_B - F₁ - F₂ - F₃, где F₁ - силы инерции, F₂ - силы внутреннего трения; F₃ - силы упругости, F_B - вынуждающая сила. Когда мгновенное значение силы превысит значение силы сухого трения в состоянии покоя, направление движения меняется. В момент t₃ скачкообразно изменяется смещение, скорость и звуковое давление (рис. 3.37). Крутизна нарастания возникающего при этом фронта импульса g_T(t) определяется верхней граничной частотой ГГ, его длительность τ_и зависит от формы АЧХ и является функцией силы внутреннего трения. Диагностическими признаками распознавания дефектов являются длительность импульсного сигнала и его полярность.

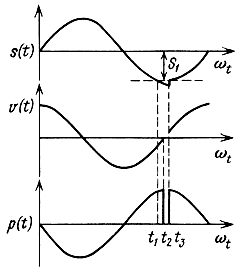
Рис. 3.37. Временные диаграммы смещения и звукового давления при сухом трении

Таким образом, при наличии сухого трения между звуковой катушкой и магнитной цепью сигнал, излучаемый ГГ, содержит периодическую последовательность импульсов дребезжания, полярность которых противоположна полярности полуволн гармонического сигнала возбуждения. При этом импульсы дребезжания возникают всегда на максимальных значениях полуволн сигнала возбуждения и их положение не зависит от его частоты и амплитуды. При сплошном трении импульсы возникают дважды за период. Амплитуда импульсов зависит от силы реакции сухого трения F′₂, амплитуды смещения и колебательной скорости. Наибольшего значения амплитуды импульсов достигают в области частоты основного (механического) резонанса.

Дребезжание из-за касания гибких выводов появляется, когда гибкие выводы (ГВ) являются одним из важнейших узлов в конструкции ГГ и в значительной степени определяют надежность, механическую прочность, уровень допустимой подводимой мощности. Кроме того, ГВ оказывают влияние на нелинейные искажения в ГГ, в частности и на нелинейные искажения, воспринимаемые как дребезжание и призвуки. В процессе работы ГВ подвергаются циклическому воздействию в диапазоне звуковых частот со стороны подвижной системы ГГ. При этом в сечениях ГГ возникают знакопеременные механические напряжения, которые могут превышать предел усталости материала применяемого шнура и приводить к его разрушению, и упругие колебания, характер которых зависит от размеров, формы, способов крепления и материала выводов [43]. При колебаниях могут возникнуть различные виды физических явлений, определяющих характер нелинейных искажений:

если ГВ касается диффузора, то наблюдается ударное дребезжание, отличающееся тем, что за один период при смещении происходит несколько упругих ударов подряд гибкого вывода о диффузор. Поскольку масса ГВ много меньше массы диффузора, резкой остановки и отсечки по смещению не происходит, поэтому в сигнале искажений формируется ряд импульсных сигналов. Этот ряд может охватывать весь фронт сигнала возбуждения, доходя до его максимального значения. Дребезжание при таком роде дефекта частотно-независимо и занимает широкую область частот от низких до средних;

в реальных ГГ гибкие выводы испытывают продольно-изгибные колебания. При монтаже вывод выполняется обычно изогнутым для обеспечения смещения подвижной системы, кроме того, он имеет сложную структуру (свивка мишурных нитей на хлопчатобумажной основе, многопроволочная жила в изоляции и т. д.), поэтому с целью упрощения задачи он рассматривается как плоско-изогнутый стержень постоянной кривизны а с физико-механическими параметрами, эквивалентными соответствующим параметрам реальных ГВ. Тогда задача может быть сведена к решению уравнения продольно-изгибных колебаний стержня:

где w - продольная (или изгибная) составляющая смещения, s - криволинейная координата, к_п, к_и - волновые числа продольных и изгибных колебаний, σ - кривизна ГВ.

Граничные условия учитывают жесткое защемление на одном конце (диффузородержателе) и возбуждение на другом (подвижной системе). Решение такой задачи позволяет определить значения резонансных частот и амплитуд вынужденных колебаний гибких выводов. Результаты расчетов показывают, что значения частот основного резонанса при длине ГВ 0,04 м находятся в пределах 30...150 Гц и сильно зависят от его кривизны. На частоте собственного резонанса амплитуда изгибных колебаний ГВ резко возрастает и может превышать амплитуду колебаний подвижной системы, при этом на максимальных смещениях может иметь место удар (касание) ГВ о подвижную систему;

в том случае, когда ГВ ни при каких условиях не соприкасаются с диффузором, резонансные колебания ГВ создают дополнительный спектр гармоник, при этом если колебания диффузора носят нелинейный характер, то при возбуждении ГВ в них возникают обертоны, которые не являются гармониками основного тона, что создает диссонирующее дребезжащее звучание.

Диагностической характеристикой импульсов возбуждения при дребезжании ГВ является их частотная селективность, которая проявляется в смещении импульсов дребезжания по сигналу U_p(t) при незначительном изменении частоты сигнала возбуждения.

Кроме вышеперечисленных дефектов анализ структуры импульсов искажения при возбуждении ГГ синусоидальном сигналом позволяет выявить и другие дефекты: отклейку шайбы, катушки; неравномерность в структуре диффузора и др. На этих различиях в структуре импульсов построен принцип работы аппаратуры УФА-1 [30], позволяющей объективно дифференцировать виды дефектов в ГГ.

У большинства ГГ, имеющих механические дефекты, при возбуждении моногармоническим сигналом одновременно с дребезжанием на некоторых частотах прослушивается специфическое звучание, воспринимаемое как призвук. В [30] предложен метод дифференцированной оценки, позволяющий объективно разделять призвук от дребезжания. В основу положено различие в спектральной характеристике: дребезжание отличается от призвука различным энергетическим распределением дискретного спектра гармоник в импульсном сигнале. Для призвука характерным является то, что основная часть энергии импульсного сигнала сосредоточена в одной - трех гармониках, для дребезжания - больше четырех. Во временной области отличия состоят в том, что у призвука затухающий колебательный процесс имеет длительность больше половины периода сигнала возбуждения; у дребезжания - длительность меньше половины. Эти различия послужили основой для определения сигнала "призвук" и "дребезжание" в ГОСТ 16122-87.

Параметрические колебания диффузоров. ("Потеря динамической устойчивости"). Одной из причин нелинейных искажений, возникающих в процессе электромеханического преобразования сигналов в ГГ, являются параметрические колебания диффузоров, обусловленные так называемым явлением "потери динамической устойчивости" в них. Проявляется это в том, что при изменении частоты и амплитуды возбуждающей силы, например при возбуждении ГГ синусоидальным сигналом, в определенных областях частот, характерных для каждого типа ГГ, и увеличении амплитуды силы выше некоторого критического значения, прослушивается "призвук", а на осциллограммах отчетливо видны колебания с частотами w/n, где w - частота вынуждающей силы, n = 2, 3, 4,... (рис. 2.10, в). Это соответствует появлению субгармонических составляющих в спектре излучаемого сигнала (рис. 2.10, а). В отличие от вынужденных, параметрические колебания поддерживаются за счет периодических изменений внутренних параметров упругой системы. Как уже было показано, диффузор ГГ можно рассматривать как тонкую упругую оболочку вращения с упругим закреплением краев, на которую действует вынуждающая сила F(w) со стороны звуковой катушки, направленная вдоль оси (см. рис. 3.26). Если разложить эту силу на две составляющие: поперечную F_u3(w), направленную по нормали к образующей диффузора, и продольную F_u1(w), направленную по касательной к ней, то поперечная сила возбуждает изгибные колебания в диффузоре с частотой со, а продольная вызывает периодическое сжатие - растяжение вдоль образующей, что можно рассматривать как эквивалентное периодическое изменение внутренней упругости оболочки. При значениях амплитуды продольной составляющей силы выше некоторого "критического" и попадании частоты в некоторую область, например вблизи удвоенной первой резонансной частоты изгибных колебаний диффузора, а также в те области, где 2w_n/Ω ≈ 1, 2, 3, исходная форма образующей σ₁, относительно которой совершаются изгибные колебания под действием силы F_u³(w), становится динамически неустойчивой, и в диффузоре возникают интенсивные (дополнительно к основным) изгибные колебания с частотой Ω. Это явление называется параметрическим резонансом или "потерей динамической устойчивости" диффузора.

Описанию параметрических колебаний диффузоров ГГ уделялось в технической литературе внимание начиная с 30-х годов [6]. Именно стремление уменьшить вероятность появления призвуков, обусловленных параметрическими резонансами, способствовало применению в массовых ГГ криволинейных диффузоров (так называемых Навье-диафрагм). Однако только развитие за последние годы общей теории динамической устойчивости упругих систем позволило перейти к количественному анализу нелинейных искажений в ГГ, обусловленных параметрическими колебаниями ("потерей динамической устойчивости") диффузоров [66].

В каждой задаче динамической устойчивости можно выделить "основное" движение, осуществляемое при любых значениях параметров, и "дополнительное", возникающее лишь при их определенных соотношениях. Первое относится к обычным вынужденным колебаниям, описываемым системой линейных дифференциальных уравнений (срединная поверхность диафрагмы занимает при этом положение σ₁). Если при некотором значении нагрузки становится возможным другая форма равновесия σ_*, (такая нагрузка называется "критической", потому что при малейшем ее превышении наступает потеря устойчивости первоначальной формы равновесия σ₁ и переход к форме σ_*), то при этом возникают "дополнительные" движения, характеризующиеся появлением интенсивных поперечных колебаний с частотой, не равной частоте возбуждающей силы. Эти колебания уже не могут быть описаны в рамках линейной теории, так как прогибы u^*_i становятся порядка толщины оболочки h. Следует отметить, что определение частотных границ областей динамической неустойчивости может быть выполнено и в рамках линейной теории, однако расчет амплитуд параметрических колебаний невозможен, так как они получаются неограниченно возрастающими. Нелинейные уравнения динамической устойчивости для случая тонкой непологой оболочки в области среднего изгиба получены с учетом характерной геометрии диафрагмы ГГ в [66].

Анализ устойчивости по полученной таким образом нелинейной системе трех дифференциальных уравнений четвертого порядка в частных производных представляет значительные трудности, поэтому в прикладных расчетах обычно ее сводят к системам обыкновенных дифференциальных уравнений. Для этого функции смещения разлагаются в ряды по фундаментальным функциям, совпадающим с формами собственных колебаний (предполагается, что формы потери устойчивости близки к формам собственных колебаний оболочки). Для диафрагм ГГ это решение ищется в виде таких же рядов, как и для расчета собственных частот [63]:

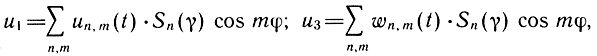
где n, m - число волн по образующей и по окружности; S_n(γ) - система функций, вид которых зависит от формы диафрагмы и граничных условий. Подставляя эти функции в полученные уравнения динамической устойчивости и применяя вариационный метод Бубнова - Галеркина, удается получить систему обыкновенных дифференциальных уравнений, которая в векторной форме может быть записана в виде:

где f - вектор перемещения, F, R - матрицы, учитывающие инерционные и упругие члены в уравнениях; N₁(t), N₂(t) - параметрические нагрузки; ψ - матрица, характеризующая нелинейность системы, K - матрица, описывающая внутренние затухания. Эта система является обобщением известного уравнения Матье-Хилла, широко используемого в различных областях физики и техники:

Особенность этого уравнения заключается в том, что при некотором соотношении между его коэффициентами оно имеет неограниченно возрастающие решения. Области неограниченно возрастающих решений отделяются от областей устойчивости периодическими решениями, поэтому определение границ областей неустойчивости сводится к отысканию условий, при которых уравнение (3.34) имеет периодические решения. Представляя решение f(t) в виде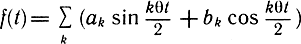  
и приравнивая коэффициенты при одинаковых степенях sin(kθt/2) и cos(kθt/2), получаем систему алгебраических уравнений, равенство нулю определителя которой позволяет вывести формулы для расчета величин критических нагрузок N_1кр и N_2кр: |R ± 1/2N₁₍₂₎S₁₍₂₎| = 0;

собственных частот: |R - F(θ/2)²| = 0;

параметрических частот θ: |R ± 1/2N₁S₁ ± 1/2N₂S₂ - F(θ/2)²| = 0.

Если выразить частоту параметрических колебаний через частоту собственных колебаний оболочки и величину критической силы N_1кр и N_2кр из (3.35), то получаются формулы для определения

первой частотой области динамической неустойчивости

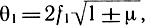
где μ = 1/2(N₁/N_1кр + N₂/N_2кр); N₁, N₂ - компоненты внешней силы, приложенной к диафрагме;

второй области неустойчивости:

Ширина областей неустойчивости убывает: Δθ/f₁ ∼ μ, μ², μ³ и т. д. Распределение трех (I, II, III) первых областей неустойчивости в плоскости параметров μ, Δθ/f₁ показано на рис. 3.38. Учет внутреннего затухания существенно снижает ширину областей неустойчивости, определение которой в этом случае производится по формуле θ₁ = 2f₁[1 ± (μ² - Δ²/π²)^0,5, где Δ - логарифмический коэффициент затухания. При наличии затухания внешняя возбуждающая сила должна быть достаточно велика, чтобы μ ≥ Δ/π, иначе параметрические колебания вообще не возникнут, поэтому увеличение внутреннего демпфирования в диафрагмах ГГ существенно снижает вероятность параметрических резонансов (а соответственно и призвуков). Поскольку диафрагма ГГ представляет собой распределенную систему, имеющую целый спектр собственных частот, области "динамической неустойчивости" могут возникать и в районе удвоенных вторых, третьих частот f₂, f₃, а также в области f₁ + f₂, f₁ + f₃ и т. д. Однако, как показали экспериментальные исследования, наибольшую "опасность" в смысле прослушивания призвуков представляет первая главная область неустойчивости θ ≈ 2f₁.

Для расчета амплитуд параметрических колебаний существенное значение имеет вид матрицы ψ(f, f′, f″), учитывающей нелинейные факторы, влияние которых увеличивается с ростом вынуждающей силы, т. е. напряжения, подводимого к звуковой катушке ГГ. Матрица ψ может быть представлена в виде:

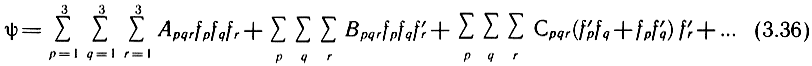
Первая группа членов, не содержащая производных от перемещений по времени, характеризует "нелинейную упругость" системы; вторая, пропорциональная скорости,- "нелинейное затухание", третья, зависящая от скорости и ускорения,- "нелинейную инерционность".

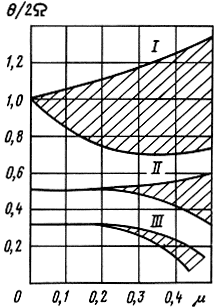
Рис. 3.38. Распределение трех первых областей 'динамической неустойчивости'

Нелинейные упругие члены появляются в уравнениях за счет нелинейных связей деформаций со смещениями, которые необходимо учитывать при прогибах, превышающих толщину оболочки. Для типичных диафрагм ГГ это условие выполняется при u^*_i > 0,2...0,3 мм. К нелинейным членам такого типа приводит учет продольных упругих связей на границах оболочки, например граничные условия на краю диафрагмы, сопряженной со звуковой катушкой (см. § 3.4). Условно этот вид зависимости можно обозначить: ψ ∼ γf³, где f - вектор смещения, γ - матрица, элементы которой получаются после подстановки в основное дифференциальное уравнение (в члены, содержащие произведения или степени от перемещений) смещений, полученных, например, по методу Бубнова-Галеркина.

Если в функцию ψ входят квадратичные члены от прогиба (т. е. ψ ∼ γ′f²), необходимо учитывать в решении (3.34) вторые гармоники, что оказывает существенное влияние на вторую область неустойчивости, т. е. асимметрия прогиба оболочки оказывает наиболее существенное влияние на параметрические колебания с частотой ω₁/4.

"Нелинейная инерционность" (третья и четвертая группы в (3.36) возникают при учете сосредоточенных масс на границах оболочки диафрагмы и сил инерции на продольных перемещениях. Условно это может быть обозначено:

где χ - матрица, полученная из членов основного уравнения, учитывающих вышеупомянутые факторы.

Наконец, при больших амплитудах необходимо учитывать не только малое расстояние энергии в материале диафрагмы, но и конечное рассеяние на границах оболочки (в упругих опорах). Вторые члены в (3.36), называемые "нелинейным затуханием", условно обозначим ψ ∼ K_Lf²f′. С учетом этих обозначений для определения амплитуды параметрического резонанса в области первой, главной, области неустойчивости используется следующая матрица:

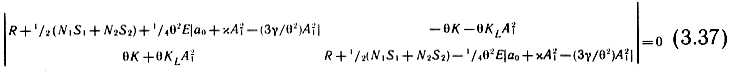
В случае, если нелинейное затухание можно не учитывать, формулы преобразуются к виду:

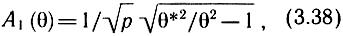
где p = χθ²/4ω₁² - 3γ/4ω₁² - первая собственная частота диафрагмы; θ - частота вынуждающей силы. Когда в оболочке преобладает нелинейная инерционность (р > 0) и наибольшие амплитуды достигаются на нижней границе области "параметрического резонанса", тогда в качестве θ^* берется верхняя граница области динамической устойчивости. При р ≤ 0, т. е. преобладании нелинейной упругости, наибольшие амплитуды достигаются на верхней границе области неустойчивости и в качестве θ* берется нижняя граница области.

Конкретный вид коэффициентов в уравнениях (3.36)-(3.38), учитывающих геометрические и физико-механические параметры криволинейных диафрагм ГГ, получены в [66], что позволило создать программы на ЭВМ и рассчитать частотные области динамической неустойчивости и амплитуды параметрических колебаний для различных типов ГГ, а также оценить влияние на них конструктивных параметров ГГ. Пример расчета первой и второй частотной области динамической неустойчивости θ_1н и θ_1В и отношения μ для громкоговорителя диаметром 152 мм (исходные параметры: радиус кривизны образующей - 160 мм, толщина 0,3 мм, материал 50% СФА - 50% СФИ целлюлозы, f₁ = 1086 Гц) показан в табл. 3.6.

Таблица 3.6

Как следует из расчетных данных, с увеличением напряжения ширина частотных областей значительно увеличивается. Расчеты позволили оценить влияние кривизны образующей. Так, переход от прямолинейной образующей R = ∞ к образующей с R = 80 мм для диаметра 152 мм приводит к сдвигу вышеуказанных областей примерно на 1000 Гц в сторону высоких частот; уменьшение диаметра ГГ, например от 152 к 80 мм, также сдвигает области неустойчивости к высоким частотам, в данном случае от 1973...2355 до 1988...2979 Гц.

Значительный объем экспериментальных исследований параметрических колебаний на больших партиях серийных ГГ, выполненный в [29, 66], показывает, что для многих типов ГГ характерны частотные области, в которых при некотором значении подводимого напряжения отчетливо прослушивается призвук, а на осциллограммах наблюдаются субгармонические колебания с частотами ω/12 и ω/4. На рис. 3.39, а показаны осциллограммы параметрических колебаний для ГГ диаметром 80 мм и области частот, где они обнаруживаются для партии серийных громкоговорителей (рис. 3.39, б), зависимость амплитуды параметрических колебаний и ширины частотной области для этого же ГГ от подводимого напряжения показана на рис. 3.39, в.

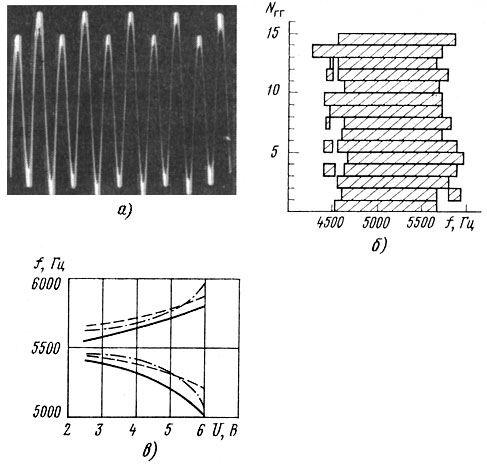
Рис. 3.39. Осциллограммы параметрических колебаний (а); области частот появления призвуков (б); зависимость ширины области и амплитуды параметрических колебаний от подводимого напряжения (в)

График зависимости амплитуды параметрических колебаний от частоты (рис. 3.40) показывает характерное явление - "явление затягивания" - для области потери динамической устойчивости: постепенное нарастание амплитуды и резкий срыв на границе области, причем характер изменений амплитуды при возрастании и снижении частоты несколько различается. Так как у всех исследованных ГГ максимальная амплитуда достигалась на верхней границе области, то преобладающее влияние в диафрагмах ГГ оказывает "нелинейная упругость". Интересно отметить, что для возбуждения субгармонических колебаний требуется некоторое конечное время воздействия сигнала определенной частоты. При быстром прохождении частоты со скоростью 5...7 с/окт субгармонические колебания возбуждаются в значительно более узких частотных областях или не возбуждаются вообще.

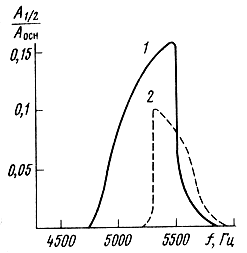
Рис. 3.40. Амплитудно-частотные характеристики параметрических колебаний: 1 - при возрастании частоты; 2 - при снижении частоты

Чаще всего субгармонические колебания возникают при значениях около 0,8 Р_н (Р_н - номинальная мощность). В некоторых, довольно редких случаях у ГГ при больших значениях напряжения могут встречаться субгармонические колебания с модуляцией, так называемый "режим биений". Спектр такого сигнала показан на рис. 2.10, осциллограмма - на рис. 3.41. Теоретическое описание "режима биений" для сложных упругих тел, в частности тонких упругих оболочек, встречает значительные трудности. Субъективно такого типа колебания воспринимаются как сильный призвук или дребезг.

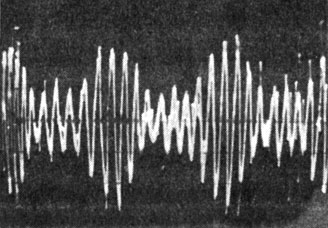
Рис. 3.41. Осциллограмма параметрических колебаний (режим биений)

Анализ полученных теоретических зависимостей, расчетные данные и большой объем экспериментальных исследований позволяют установить связь характеристик параметрических колебаний диффузоров с их конструктивными и физико-механическими параметрами и выявить факторы, оказывающие наибольшее влияние на снижение уровня призвуков в ГГ.

"Нелинейная упругость" оказывает существенное влияние на величину амплитуды параметрических колебаний, а следовательно, и на вероятность появления призвуков, поэтому все меры, направленные на повышение общей жесткости диффузоров, являются чрезвычайно эффективными, поскольку увеличиваются значения резонансных частот диффузоров и области "динамической неустойчивости" сдвигаются в более высокочастотную часть спектра, амплитуды параметрических колебаний значительно уменьшаются. Наибольшее влияние оказывает увеличение радиуса кривизны образующей, выбор соответствующего распределения плотности и модуля Юнга (за счет выбора материалов и пропиток для диффузоров, увеличивающих их жесткость), а также расположения различных ребер жесткости на диффузоре.

"Линейное демпфирование" за счет внутреннего трения в материале оказывает значительное влияние на величину амплитуды параметрических колебаний. Эксперименты показали, что увеличение коэффициента демпфирования в диффузоре за счет пропиток от 0,02 до 0,06 позволило снизить амплитуду параметрических колебаний в 7 раз. Кроме того, величина демпфирования определяет пороговый уровень силы, необходимой для возникновения параметрических колебаний, т. е. чем выше декремент затухания, тем больше должно быть приложенное напряжение, чтобы этот вид колебаний вообще мог возникнуть. Увеличение демпфирования в системе ограничивает явление "затягивания" параметрических колебаний за пределы областей неустойчивости, поэтому все меры, направленные на повышение внутреннего демпфирования в диффузоре (выбор пропиток, специальных материалов и пр.), уменьшают вероятность появления призвуков.

"Нелинейное демпфирование" уменьшает амплитуду параметрических колебаний пропорционально А₁ ∼ 1/(Δ_L)^0,5; где Δ_L - декремент нелинейного затухания. Увеличение нелинейного демпфирования может быть достигнуто за счет нанесения демпфирующих смазок на подвес, применения для подвесов соответствующих материалов с большим внутренним трением (резина, прорезиненные ткани и т. д.). Экспериментальные результаты показывают достаточную эффективность этих средств в снижении призвуков.

"Нелинейная инерционность" также вносит свой вклад в увеличение амплитуд параметрических колебаний, уменьшение ее может быть достигнуто за счет снижения граничных масс (рационального распределения массы между подвесами, катушкой и диффузором) и увеличения жесткости подвеса в окружном направлении.

В заключение следует отметить, что, как показывает практика, определенный уровень призвуков прослушивается у подавляющего большинства серийных ГГ. Важной задачей при проектировании громкоговорителей является выбор такой совокупности конструктивных и физико-механических параметров, чтобы уровень критической нагрузки диффузоров Р_кр, ниже которой появление призвуков этого типа маловероятно, соответствовал номинальной или даже максимальной синусоидальной мощности громкоговорителей, тогда при проведении любых видов испытаний ГГ призвуки этого типа прослушиваться не будут. Если это не удается, необходимо стремиться увеличить общее демпфирование в подвижной системе для максимального снижения амплитуды параметрических колебаний, т. е. слышимости призвуков.

Нелинейные процессы, связанные с эффектом Доплера в громкоговорителях. Характерной особенностью электродинамических ГГ является возникновение в них интермодуляционных искажений, обусловленных как амплитудной, так и частотной модуляцией сигнала. Искажения, определяющие амплитудную модуляцию излучаемых сигналов, обусловливаются нелинейностью упругих характеристик подвижных систем ГГ и нелинейностью его электромагнитных параметров. Частотная модуляция сигналов, возникающая в ГГ, связывается с эффектом Доплера. Последний представляет собой давно известное в физике явление, заключающееся в том, что при наличии источника колебаний с частотой f₀, движущегося со скоростью V₀ относительно неподвижного приемника в среде, где с - фазовая скорость распространения колебаний, происходит изменение длины волны и соответственно частоты излучаемых колебаний: f = f₀/[1 ± (V₀/c)]. Процессы, происходящие в ГГ при одновременном воспроизведении им широкого спектра частот и приводящие к модуляционному воздействию низкочастотной части спектра на высокочастотную, обычно объясняются с помощью эффекта Доплера.

Созданные за последние годы методики измерений AM и ЧМ искажений позволили количественно оценить их в серийных громкоговорителях. Характер частотной зависимости AM и ЧМ искажений в коаксиальном ГГ показан на рис. 2.14. Частотно-модулированный сигнал может быть записан следующим образом:

где р_m - амплитуда излучаемого сигнала; f₂ - модулируемая (высокая) частота, f₁ - модулирующая (низкая) частота; m - индекс модуляции, ψ - начальный сдвиг фазы. Для оценки величины искажений Доплера в ГГ были предложены различные критерии, например

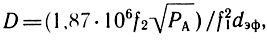
где D - фактор искажений, соответствующий отношению мощности боковых полос к мощности модулируемой частоты, %; Р_А - акустическая выходная мощность на частоте f₁, Вт; d_эф - эффективный диаметр диффузора, мм. Кроме того, используется такой критерий, как D = 1129f₂/(1129 + X_maxπf₁), где Х_mах - максимальная амплитуда смещения, мм, и др. Однако выбор критериев оценки ЧМ искажений в ГГ нельзя считать окончательно установленным. Несмотря на большой комплекс работ, посвященный исследованию вопросов субъективной оценки доплеровских искажений в ГГ, полученные результаты противоречивы, поскольку применялись различные методики и аппаратура. Предварительно установленными можно считать следующие данные по порогам слышимости: на двух чистых тонах не свыше 1%, в музыке 8...9%. В последние годы была предложена физическая интерпретация эффекта Доплера как фазовой модуляции излучаемого ГГ сигнала в точке приема, что объясняет ряд полученных ранее противоречивых результатов.

Таким образом, несмотря на многолетние исследования, посвященные возникновению в ГГ нелинейных искажений за счет эффекта Доплера, остаются нерешенными существенные вопросы, требующие дополнительного анализа: разработка точных количественных критериев для расчета D в ГГ и установление их связи с конструктивными параметрами диффузоров; установление субъективных порогов восприятия D при работе ГГ, разработка перспективной методики их измерений в реальных ГГ и рекомендаций по их уменьшению.