1.5. Отражательные решетки

Отражательные решетки ПАВ являются основным элементом резонаторов на ПАВ. Они образуются периодическими нарушениями структуры поверхности пьезокристалла и представляют собой распределенный отражатель с пространственным периодом, равным обычно половине рабочей длины ПАВ. Каждый из его элементов отражает лишь малую часть падающей на него акустической волны. Однако за счет синфазного сложения большого числа отраженных частичных волн общий коэффициент отражения на рабочей частоте получается близким к единице, но и существенно частотно-зависящим, так как синфазное сложение возможно лишь вблизи рабочей частоты решетки.

Неоднородности структуры поверхности пьезокристалла, необходимые для реализации отражающих решеток, можно создать разными способами, например, нанесением на его поверхность проводящих или непроводящих полосок. В первом случае металлические полоски закорачивают электрическое поле в той части поверхности пьезокристалла, на которую они нанесены, что, в основном, и вызывает локальное изменение скорости ПАВ. Во втором случае неоднородность создается за счет внесения дополнительной массовой нагрузки на поверхность пьезокристалла. Нарушение структуры поверхности может быть также создано путем травления или фрезерования канавок. Иногда для тех же целей используют ионную имплантацию или диффузию металла [33, 44, 45].

Принцип действия отражательных решеток ПАВ во многом аналогичен принципу действия обычных отражательных антенных решеток. Отличительной их чертой является большое число отражающих элементов (несколько сотен) и очень малый коэффициент отражения каждого элемента решетки (меньше одного процента).

Рассмотрим действие распределенного отражателя на модели отражательной решетки, выполненной в виде неоднородной линии передачи ПАВ [44], характеристическое сопротивление которой (рис. 1.15) периодически скачком изменяется от z₀₁ до z₀₂. Как показывает анализ, проведенный в [44], такая отражательная решетка имеет модуль коэффициента отражения ρ, определяемый из выражения

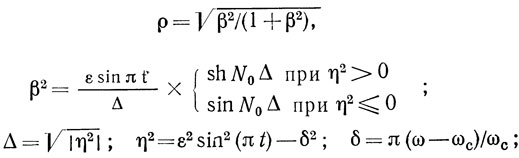
N₀ - количество отражающих полосок; ω_с - центральная частота отражения; Δω = ω - ω_с.

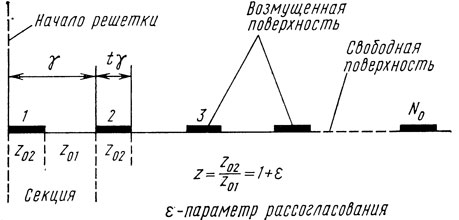
Рис. 1.15. Модель отражательной решетки в виде периодически рассогласованной линии передачи

Выражения (1.23) получены для расстроек, удовлетворяющих условию |δ| ≤ 0,4. Кроме того, при их выводе предполагалась, что выполняется неравенство 0,3 ≤ t ≤ 0,7 (рис. 1.15).

Фаза коэффициента отражения при t = 0,5 определяется из выражения

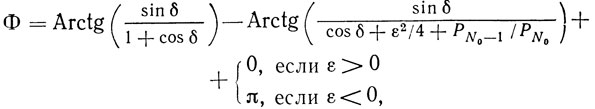
где

Для t ≠ 0,5 выражение (1.24) на частоте ω_с справедливо с точностью до 1°, если заменить ε на ε sin πt.

Зависимости модуля и фазы коэффициента отражения от частоты приведены на рис. 1.16, а, б. Как видно из рисунка, зависимость модуля коэффициента отражения имеет вид функции sin x/x с уплощенной вершиной. Максимально значение

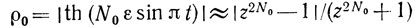
модуль коэффициента отражения принимает, когда отраженные от каждой полоски акустические волны складываются синфазно. Это происходит на частоте ω_с, которая определяется периодом отражательной решетки d:

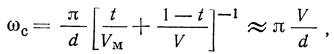
где V и V_м - скорости ПАВ на свободной и металлизированной поверхности пьезоэлектрика. Приближенное равенство в (1.26) переходит в точное при t = 0,5. Зависимость модуля коэффициента отражения на частоте ω_с от N_0ε приводится на рис. 1.17.

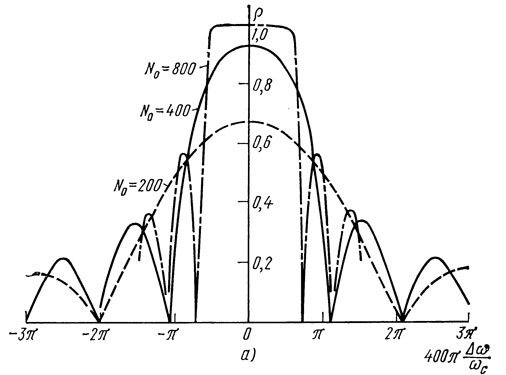
Рис. 1.16. Зависимость модуля (а) коэффициента отражения периодической структуры от частоты при ε = 0,004 и t = 0,5

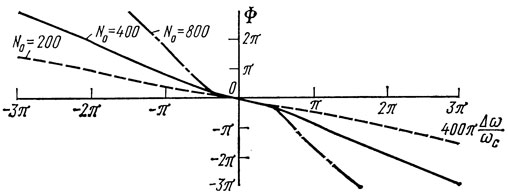
Рис. 1.16. Зависимость фазы (б) коэффициента отражения периодической структуры от частоты при ε = 0,004 и t = 0,5

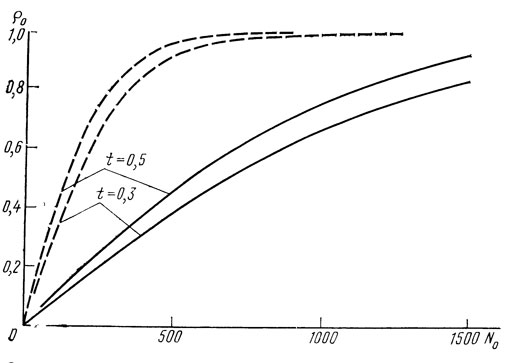
Рис. 1.17. Зависимость модуля коэффициента отражения периодической структуры на центральной частоте от количества отражающих элементов при ε = 0,004

Из выражения (1.23) нетрудно определить полосу отражения по нулям частотной зависимости главного лепестка модуля коэффициента отражения

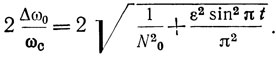
Видно, что при N → ∞ полоса отражения (1.28) равна

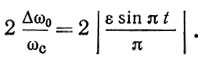
Проанализируем зависимость фазы коэффициента отражения от частоты. Так как параметр рассогласования отражательной решетки ε мал (|ε| ≤ 0,05), а полоса отражения узкая, то в пределах главного лепестка частотной зависимости коэффициента отражения второе слагаемое в (1.24) будет превалировать над первым и определять частотную зависимость фазы коэффициента отражения. Из рис. 1.16 видно, что вблизи центральной частоты фаза коэффициента отражения изменяется линейно с угловым коэффициентом

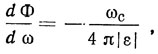
а на границе полосы отражения принимает значение

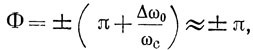
где Δω₀/ω_с - относительная полоса отражения (1.28).

Для области частот, далеких от центральной частоты (где модуль коэффициента отражения мал), зависимость фазы коэффициента отражения стремится к прямой с наклоном

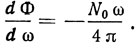
Отмеченная выше линейная зависимость фазы (коэффициента отражения от частоты (1.30) позволяет для частот, близких к центральной частоте ω_с, заменить распределенный отражатель яз резонаторе ПАВ обычным зеркалом с коэффициентом отражения ρ₀, но смещенным относительно начала решетки на расстояние λ/4 |ε|, где λ - длина поверхностной волны на частоте ω_с. Смещение эквивалентного зеркала связано с тем, что поверхностная акустическая волна при падении на периодическую отражательную решетку достаточно глубоко проникает в нее, и тем глубже, чем меньше ε.

Как следует из (1.26) при t = 0,5 и N₀ → ∞ коэффициент отражения на частоте ω_с достигает максимального значения, равного 1. Это справедливо, если потери в отражательной решетке отсутствуют. В действительности они всегда есть из-за потерь в металлических полосках, возбуждения объемных волн и т. д. Потери оцениваются коэффициентом погонного затухания а, который обычно много меньше параметра рассогласования ε. Например, для Al-полосок на YZ-срезе LiNbO₃ коэффициент погонного затухания равен приблизительно 5,8⋅10^-4, а ε ≈ 0,01 [44]. Учет потерь при α << |ε|, t = 0,5 дает следующие соотношения для модуля и фазы коэффициента отражения решетки на центральной частоте [44]:

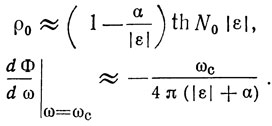
То, что модуль коэффициента отражения не достигает значения, равного единице, определяет конечное значение добротности резонатора. Как будет показано ниже, добротность рассматриваемого резонатора ПАВ

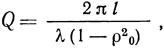
где l - эффективная линия полости резонатора с учетом проникновения ПАВ внутрь решеток. Тогда, используя (1.32), для N₀ → ∞ получаем

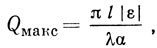
а для конечного числа отражателей в решетке при εN₀ > 1 имеем

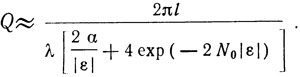
Введем коэффициент q = Q/Q_макс, показывающий насколько близка добротность реального резонатора с конечным числом отражателей к добротности резонатора с N₀ → ∞:

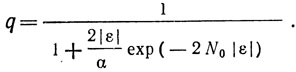
Зависимость q от εN₀ для различных отношений α/|ε| приводится на рис. 1.18, из которого видно, что существует некоторое оптимальное число отражателей в решетке N_опт, при котором q достаточно близко к 1, и дальнейшее увеличение числа отражателей приводит лишь к незначительному его- увеличению. Обычно N_опт определяют для q = 0,9. Например, если α = 5,8⋅10^-4, ε = 0,01, то N_опт = 290.

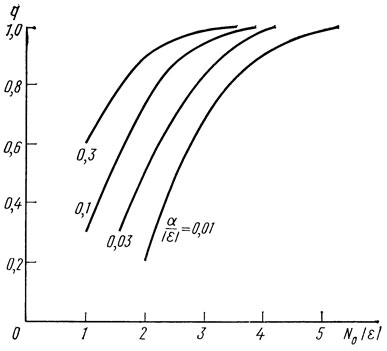
Рис. 1.18. Зависимость q = Q/Q_макс от N₀|ε| для различных значений α/|ε|