1.7. Эквивалентная схема и характеристики одновходового резонатора

Перейдем теперь непосредственно к эквивалентным схемам резонаторов ПАВ. Рассмотрим вначале одновходовый резонатор. Очевидно, что его можно представить следующей эквивалентной электрической схемой (рис. 1.21) [45]. На этой схеме встречно-штыревой преобразователь представлен эквивалентной трехполюсной электрической схемой, рассмотренной в § 1.2. Акустически входы преобразователя через отрезки звукопроводов нагружены на входные проводимости отражательных решеток Y_р1 и Y_р2.

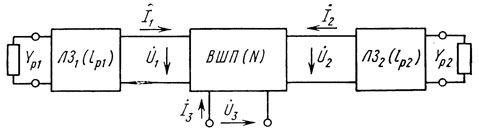
Рис. 1.21. Эквивалентная электрическая схема одновходового резонатора ПАВ

Звукопровод между преобразователем и решетками на рис. 1.21 отражается включением между Y_р1 или Y_р2 и преобразователем электрического аналога звукопровода - отрезка длинной линии с характеристическим сопротивлением z₀ и длиной l_p1 или l_р2. Входная проводимость отражательных решето к Y_р1 и Y_р2 может быть легко определена по известному коэффициенту отражения

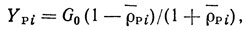
где G = 1/z₀; ρ‾_рi - комплексный коэффициент отражения i-й отражательной решетки.

Используя эквивалентную схему на рис. 1.21, нетрудно получить выражение для входной проводимости резонатора ПАВ [45]:

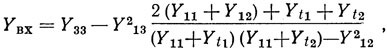
где Y₃₃, Y₁₁, Y₁₃ и Y₁₂ - элементы матрицы Y-параметров ВШП; Y_ii = G₀(1 - ρ‾_i)/(1 + ρ‾_i) - входная проводимость i-й отражательной решетки с учетом отрезка звукопровода, непосредственно нагружающая i-й акустический вход ВШП; ρ‾_i = ρ‾_piехр(-j2kl_pi) - комплексный коэффициент отражения решетки с учетом отрезка звукопровода; k = 2π/λ - волновое число; i = 1, 2.

Обычно одновходовые резонаторы симметричны, т. е. l_р1 = l_р2 = l_р и N₀₁ = N₀₂ = N₀. Кроме того, их частотные свойства (как отмечалось выше) определяются в основном резонансной полостью и отражательными решетками, которые имеют существенно более узкие полосы отражения по сравнению с полосой пропускания преобразователя. Это позволяет считать, что ВШП резонатора работает точно на частоте акустоэлектрического синхронизма. Как и ранее, воспользуемся моделью преобразователя с поперечным распределением поля [39]. При этом с учетом сказанного выражение для Y_вх (1.40) упрощается и принимает вид

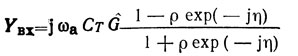
где ρ - модуль коэффициента отражения; η - полный набег фазы ПАВ при распространении от преобразователя до решетки и обратно с учетом потери фазы при отражении; η = 2kl_p - Ф = 2kl_э = 4π ω/ω_c М_э; М_э - количество длины волн частоты ω_с, укладывающихся на l_э = l_p - Ф/2k - эквивалентном расстоянии от отражательной решетки до преобразователя с учетом фазы отражения.

Разделяя (1.41) на действительную и мнимую части, получим

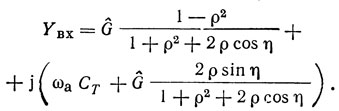
Зависимости активной и реактивной составляющих входной проводимости одновходового (резонатора от частоты приведены на рис. 1.22, из которого видно, что зависимость входной проводимости резонатора от частоты имеет период Δω_пер/ω_с = 1/2М_э. Резонансные свойства резонатора ПАВ выражены тем резче, чем ближе к 1 модуль коэффициента отражения ρ₀ (т. е. чем больше число отражателей N₀ в решетке) и чем меньше Q_r (т. е. чем больше число пар электродов N в преобразователе).

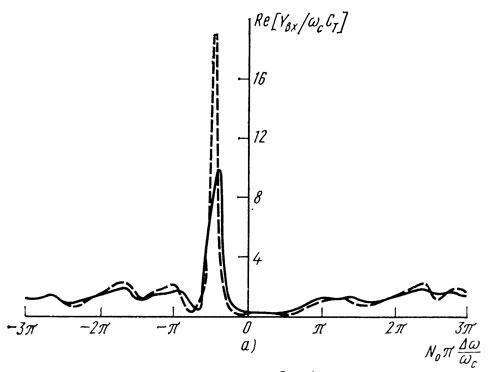
Рис. 1.22. Зависимость активной (а) и реактивной (б) составляющих входной проводимости одновходового резонатора ПАВ (материал подложки LiNbO₃) от частоты при N₀ = 400, N = 22, l_р = 27,875λ_с, k²_m = 0,0482: ----- е = 0,003; - - - е = 0,004

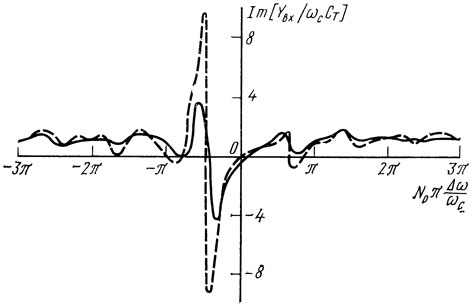
Рис. 1.22. Зависимость активной (а) и реактивной (б) составляющих входной проводимости одновходового резонатора ПАВ (материал подложки LiNbO₃) от частоты при N₀ = 400, N = 22, l_р = 27,875λ_с, k²_m = 0,0482: ----- е = 0,003; - - - е = 0,004

Проанализируем выражение (1.42). Для простоты будем считать, что модуль коэффициента отражения ρ не зависит от частоты и равен ρ₀. Рассмотрим мнимую часть входной проводимости. Ее зависимость от частоты определяется составляющей

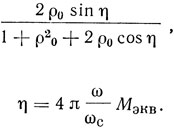
В дальнейшем нас будут интересовать частоты, на которых реактивная составляющая входной проводимости обращается в нуль. Эти частоты находятся из уравнения

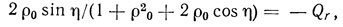
где Q_r = ωC_T/G = π/4k²_mN - электрическая добротность преобразователя.

Графическое решение уравнения (1.43) приводится на рис. 1.23. Левая часть (1.43) принимает максимальное значение 2ρ₀/(1 - р²₀) при η = 2nπ + arc cos[- 2ρ₀/(1 + p²₀)] и минимальное - 2ρ₀/(1 - р²₀) при η = 2πn - arc cos[ -2ρ₀/(1 + р²₀)]. Активная составляющая входной проводимости резонатора (1.42) принимает максимальное значение G(1 + ρ₀)/(1 - ρ₀) при η = π + 2πn и минимальное G(1 - ρ₀)/(1 + ρ₀), при η - 2πn.

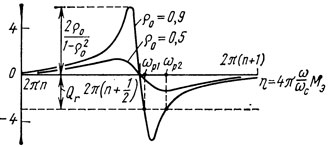
Рис. 1.23. Периодическое решение уравнения (1.43), определяющее собственные частоты резонатора ПАВ при ρ = const

Зависимость активной составляющей входной проводимости резонатора от частоты при ρ(ω) = ρ₀ изображена на рис. 1.24. Как видно из рис. 1.23, 1.24, на резонансной частоте ω_p1 активная составляющая проводимости резонатора близка к максимальной, а на ω_p2 - к минимальной. Назовем частоту ω_p1 - частотой последовательного резонанса, а ω_p2 - параллельного, поскольку типы колебаний на этих частотах соответствуют резонансам тока и напряжения со стороны электрического входа резонатора.

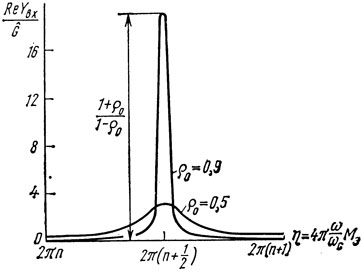
Рис. 1.24. Зависимость активной составляющей входной проводимости резонатора ПАВ от частоты при ρ = const

Эквивалентной схемой для резонанса тока является последовательный электрический контур, а для резонанса напряжений - параллельный. Резонанс тока (или последовательный резонанс) соответствует наименьшему входному сопротивлению резонатора, резонанс напряжения - наибольшему. Таким образом, при резонансе тока напряжение на электродах преобразователя близко к нулю. Очевидно, что это может быть лишь при условии, соответствующем рис. 1.25, а. При изменении частоты изменяется структура электрического поля преобразователя и наступает момент, когда она соответствует рис. 1.25, б. В этом случае напряжение на электродах преобразователя максимально, что соответствует резонансу напряжения (или параллельному резонансу).

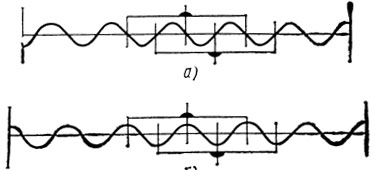
Рис. 1.25. Структура поля при последовательном (а) и параллельном (б) резонансах в резонаторе ПАВ

Как следует из уравнения (1.43) и рис. 1.23, условием возникновения резонанса в одновходовом резонаторе является неравенство

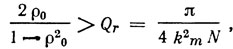
которое накладывает ограничение на минимальное число пар штырей N в преобразователе. Например, при коэффициенте отражения решеток ρ₀ = 0,964 для береза кварца требуется, чтобы преобразователь имел число пар штырей не менее

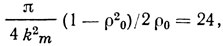
а для ниобата лития при тех же условиях требуется, чтобы N ≥ 1. Частоты параллельного и последовательного резонансов определяются из решения уравнения (1.43), которое может быть записано в виде

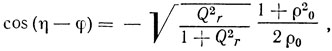
где

Из (1.45) легко определить η_пap и η_посл:

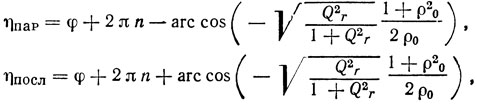
а также относительную разницу по частоте между параллельным и последовательным резонансами

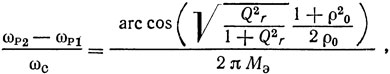
где М_э = l_э/λ - количество длин волн, укладывающихся на частоте ω_с на эквивалентной длине l_э.

Из (1.47) следует, что частоты последовательного и параллельного резонансов отстоят друг от друга тем дальше, чем меньше М_э и чем длиннее преобразователь (чем Q_r меньше). Максимальная разность между частотами резонансов

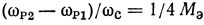
достигается при Q_r → 0, т. е. при k²_mN → ∞.

Выражение (1.47) получено в предположении, что ρ и М_э не зависят от частоты. Для реальных резонаторов ПАВ это несправедливо, и поэтому его следует рассматривать лишь как оценку относительной разности между частотами последовательного и параллельного резонансов узкополосного резонатора ПАВ. Отметим, что из-за того, что эффективность преобразования электромагнитной энергии в энергию поверхностных волн существенно меньше, чем для акустических объемных волн, частоты последовательного и параллельного резонансов в резонаторах ПАВ расположены ближе друг к другу, чем в резонаторах на объемных типах волн [45].

Резонатор будет иметь только одну частоту последовательного и одну частоту параллельного резонанса, если собственные частоты соседних мод резонатора будут приходиться на области частот, где коэффициент отражения решетки близок к нулю. Для этого должно выполняться равенство

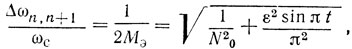
где М_э = l_э/λ.

Очевидно также, что резонатор будет однорезонансный, если левая часть (1.48) существенно превышает правую, т. е. если полоса отражения решетки существенно меньше межмодового расстояния резонатора.

Из рис. 1.22 видно, что вдали от резонансных частот входная проводимость одновходного резонатора соизмерима с проводимостью резонатора вблизи частоты параллельного резонанса, т. е. резонатор плохо фильтрует вдали от резонансной частоты. Такой ход частотной зависимости входной проводимости одновходового резонатора объясняется узкополосностью отражающих решеток резонаторов. Действительно, вдали от центральной частоты отражения решеток они не отражают падающие на них ПАВ, что и приводит к тому, что резонатор представляет в этом случае лишь широкополосный ВШП, который, безусловно, не может обеспечить необходимую фильтрацию частот, далеко отстоящих от резонансных. Особенно это заметно в системах, где резонатор используется вблизи частоты параллельного резонанса. Например, в автогенераторе на таком резонаторе при работе вблизи параллельного резонанса из-за плохой фильтрации могут возбудиться паразитные колебания, частоты которых далеки от резонансной частоты резонатора. В то же время даже у обычного LC-контура проводимость вдали от резонансной частоты существенно превышает его проводимость в полосе пропускания. Это обеспечивает лучшую по сравнению с одновходовым резонатором фильтрацию далеко отстоящих от резонансной частоты составляющих колебания и препятствует возникновению паразитных колебаний. С этой точки зрения более целесообразным видится применение одновходового резонатора ПАВ вблизи частоты последовательного резонанса.

Интересно сравнить частотные зависимости одновходового резонатора ПАВ с соответствующими зависимостями обычного кварцевого резонатора на объемных типах колебаний. Отметим следующие основные особенности. В резонаторе ПАВ полосы пропускания параллельного и последовательного резонансов перекрываются, что дает возможность говорить о полосе пропускания резонатора ПАВ, внутри которой расположена частота последовательного и параллельного резонансов. В традиционных же кварцевых резонаторах из-за их существенно более высокой добротности эти полосы разнесены далеко друг от друга и не перекрываются, хотя процентное отношение разности частот последовательного и параллельного резонансов к их среднему значению как для резонаторов ПАВ, так и для обычных кварцевых резонаторов приблизительно равны и составляют десятые доли процента.

Второй существенной особенностью резонаторов ПАВ является то, что в пределах полосы пропускания его активные составляющие входной проводимости и входного сопротивления существенно зависят от частоты. У кварцевого резонатора на объемных типах колебаний эта зависимость значительно меньше.

Рассмотрим фазовую характеристику одновходового резонатора на рис. 1.19:

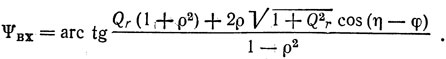
Видно, что максимальное и минимальное значение фаза принимает при

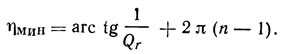
Эти значения равны соответственно

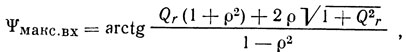
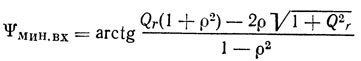
и близки к 90° только при ρ, близком к 1, т. е. только для частот, расположенных в главном лепестке частотной зависимости коэффициента отражения.

Определим крутизну фазовой характеристики одновходового резонатора на резонансных частотах:

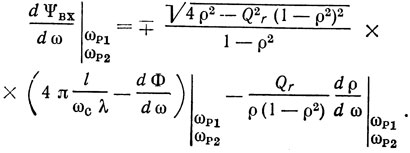
Знак минус в выражении (1.50) относится к ω_p1 - частоте последовательного резонанса, а плюс - к частоте параллельного резонанса ω_p2.

Из (1.50) можно определить добротность резонатора по формуле

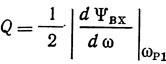
Предполагая, что Q_r(1 - р²₀) << 1, т. е. условия возникновения резонанса (1.44) заведомо выполнены, а также учитывая, что р₀ ≈ 1 и ω_p1 = ω_c, т. е.

dρ/dω|_ωp1 = 0, из (1.51) (1.50) получаем

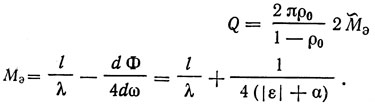
Полученное выражение позволяет для частот, близких к частоте резонанса заменить одновходовый резонатор эквивалентной схемой, изображенной на рис. 1.26 [45-47]. На этом рисунке С_Т - статическая емкость преобразователя, R = 1/G - сопротивление излучения ВШП на частоте акустоэлектрического синхронизма. Последовательный контур, образованный L₁, C₁ и r₁, отображает свойства резонатора вблизи частоты последовательного резонанса ω_p1. Параметры этого контура равны:

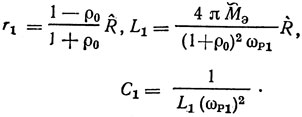
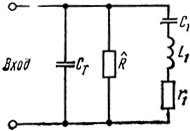
Рис. 1.26. Эквивалентная электрическая схема замещения резонатора ПАВ вблизи частоты последовательного резонанса