1.8. Эквивалентная схема и характеристики двухвходового резонатора

Перейдем к рассмотрению двухвходового резонатора ПАВ, изображенного на рис. 1.19. Его эквивалентная схема показана на рис. 1.27. Она аналогична эквивалентной схеме ЛЗ ПАВ на рис. 1.10 с тем отличием, что внешние акустические входы преобразователей нагружены не на характеристическую проводимость акустической среды G₀ = 1/z₀, а на входные проводимости отражательных решеток Y_р1 и Y_р2, которые подключены к внешним акустическим входам преобразователей отрезками длинных линий с характеристической проводимостью G₀ и длинами l_p1 и l_p2.

Рис. 1.27. Эквивалентная электрическая схема двухвходового резонатора ПАВ

Поскольку, как отмечалось выше, в предположениях мэзоновской модели ВШП [39] короткозамкнутый преобразователь не вызывает отражений ПАВ и эквивалентен отрезку линии передачи длиной l_i, для определения собственных проводимостей резонатора Y₁₁, Y₂₂ получим эквивалентную схему, аналогичную эквивалентной схеме одновходового резонатора. При этом выражения для собственных проводимостей двухвходового резонатора будут иметь вид (1.40). Предполагая [как и при получении выражения для входной проводимости одновходового резонатора (1.41)], что полоса отражения решеток существенно уже полосы пропускания преобразователей и центральная частота отражения решеток ω_с равна частоте акустоэлектрического синхронизма ВШП ω_а, для одинаково расположенных относительно преобразователей отражающих решеток (ρ¯₁ = ρ¯₂ = ρ¯, l_p1 = l_p2 = l_p) получим

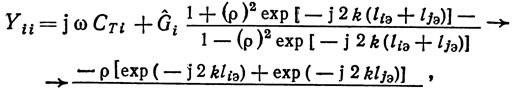
где

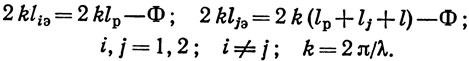
Выражение для взаимной проводимости Y₁₂ матрицы Y-параметров двухвходового резонатора может быть получено из анализа эквивалентной схемы на рис. 1.27 аналогично § 1.4, где исследовалась ЛЗ ПАВ, и при сделанных выше предположениях может быть записано в виде

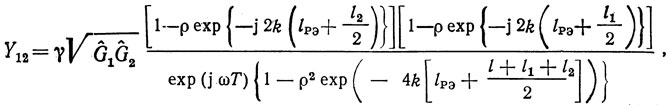
где

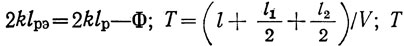
- время задержки ПАВ при распространении между центрами преобразователей; l_i = N_iλ - длина i-го преобразователя.

Проанализируем выражения (1.54) и (1.55). Рассмотрим для простоты симметричный двухвходовый резонатор (l₁ = l₂ = l_п). Собственные проводимости резонатора будут равны:

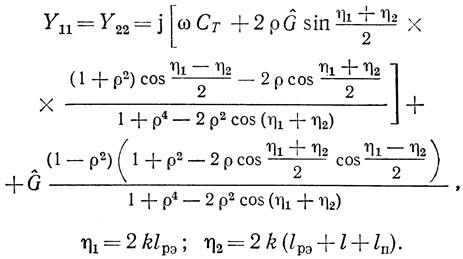
Из (1.56) видно, что частотные зависимости собственных проводимостей двухвходового резонатора более сложны, чем соответствующие частотные зависимости одновходового резонатора. Это объясняется несимметрией образующегося при коротком замыкании одного из ВШП эквивалентного одновходового резонатора.

Зависимости активной и реактивной составляющих собственной проводимости Y₁₁ для двухвходового резонатора (рис. 1.19) от частоты приведены на рис. 1.28.

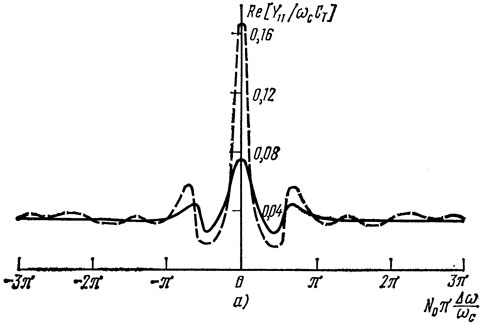
Рис. 1.28. Зависимость активной (а) и реактивной (б) составляющих собственной проводимости симметричного двувходового резонатора ПАВ (материал подложки ST-срез кварца) от частоты; при N₀ = 400, N = 22, l_p = 3,75λ, l = 48,5λ, k²_m = 0,0012: ---- ε = 0,001; - - - ε = 0,002

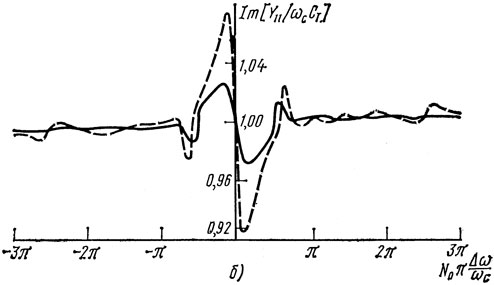
Рис. 1.28. Зависимость активной (а) и реактивной (б) составляющих собственной проводимости симметричного двувходового резонатора ПАВ (материал подложки ST-срез кварца) от частоты; при N₀ = 400, N = 22, l_p = 3,75λ, l = 48,5λ, k²_m = 0,0012: ---- ε = 0,001; - - - ε = 0,002

Выражение для взаимной проводимости Y₁₂ симметричного двухвходового резонатора примет вид:

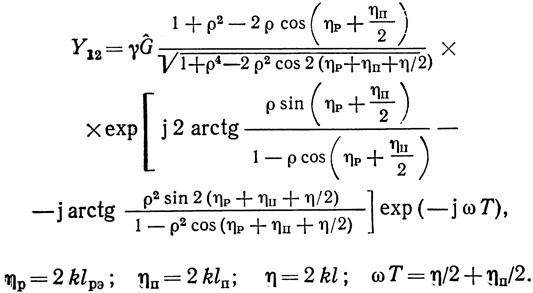
Зависимость модуля и фазы взаимной проводимости двухвходового резонатора от частоты приводится на рис. 1.29.

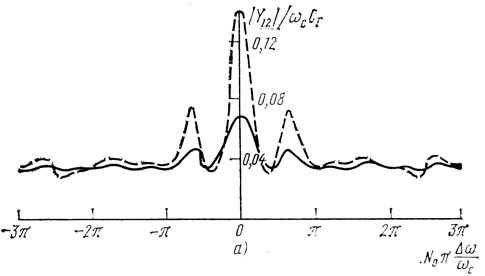
Рис. 1.29. Зависимость модуля (а) и фазы (б) взаимной проводимости симметричного двувходового резонатора ПАВ (материал подложки ST-срез кварца) от частоты; при N₀ = 400, N = 22, l_р = 3,75λ, l = 48,5λ, k²_m = 0,0012: ------ ε = 0,001; - - - ε = 0,002

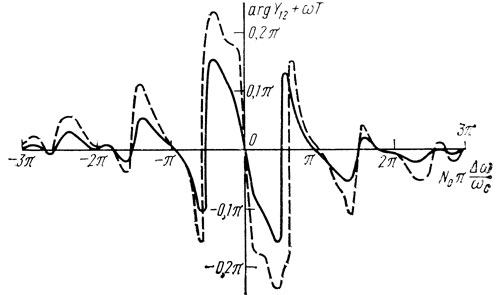
Рис. 1.29. Зависимость модуля (а) и фазы (б) взаимной проводимости симметричного двувходового резонатора ПАВ (материал подложки ST-срез кварца) от частоты; при N₀ = 400, N = 22, l_р = 3,75λ, l = 48,5λ, k²_m = 0,0012: ------ ε = 0,001; - - - ε = 0,002

Из (1.57) видно, что |Y₁₂| принимает максимальное значение, если cos(η_p + η_п/2) = - 1, а cos 2(η_p + η_п - η/2) = 1. Последнее означает, что

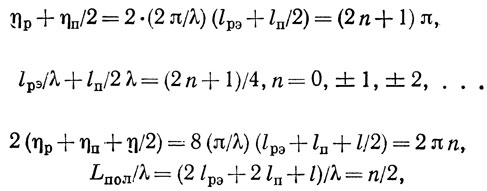
где L_пол = 2l_рэ + 2l_п + l - длина резонансной полости резонатора ПАВ.

Как видно из (1.38), условие (1.59) соответствует условию резонанса в полости резонатора. Условие (1.58) соответствует расположению центра преобразователя в пучности стоячей поверхностной волны. Максимальное значение |Y₁₂| при ω_р = ω_с равно

Соответственно, если cos (η_p + η_п/2) = 1, а cos 2(η_p + η_п + η/2) = -1, то получаем минимальное значение |Y₁₂|, равное

Это значение |Y₁₂| достигается при

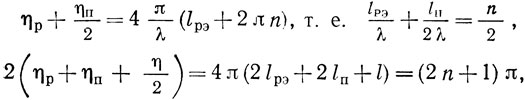
т. е.

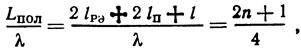
где λ - длина ПАВ на частоте ω_с.

Определим крутизну фазовой характеристики

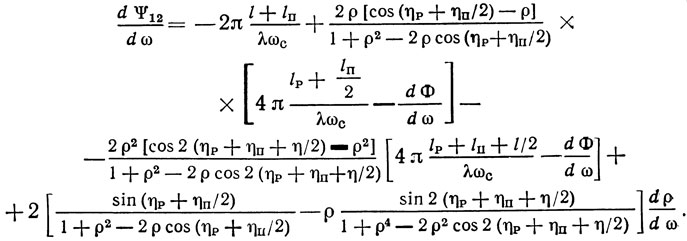
Из (1.62) при ω = ω_макс = ω и ω = ω_мин = ω_с получаем

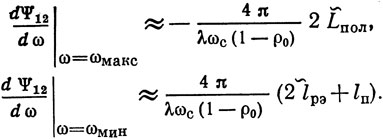
Из (1.63) и (1.64) видно, что крутизна фазовой характеристики в точке, где |Y₁₂| принимает значение |Y₁₂|_макс больше, чем в точке |Y₁₂| = |Y₁₂|_мин.

По известным Y-параметрам двухвходового резонатора могут быть определены его коэффициенты передачи и входные сопротивления. Так, для схемы включения генератора и нагрузки на рис. 1.11 коэффициенты передачи по напряжению и току с первого входа резонатора ПАВ на его второй вход имеют вид (1.18), а выражение для коэффициента передачи по мощности имеет вид (1.19). Выражения для входных проводимостей резонатора ПАВ с нагруженным вторым входом имеют вид, также аналогичный (1.20).

Пример зависимости модуля и фазы K²¹_U от частоты для симметричного резонатора ПАВ показан на рис. 1.30. Расчет проводился для случая Y_н = g_н = ω_c С_Т и Z_Г = 0. Из рис. 1.30 видно, что если условие появления резонансов для собственной проводимости (1.44) не выполняется, то вид частотной зависимости коэффициента передачи по напряжению определяется зависимостью от частоты функции Y₁₂(ω).

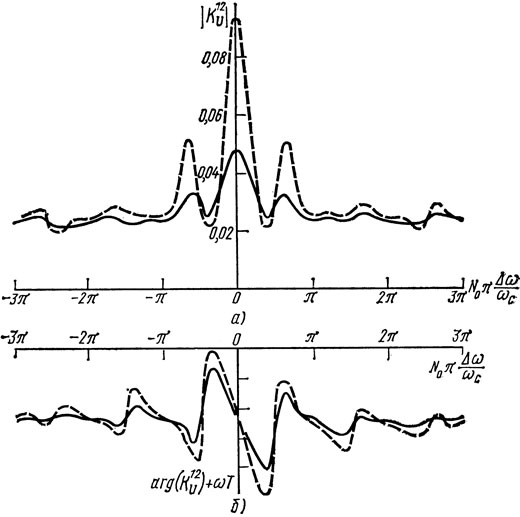
Рис. 1.30. Зависимость модуля (а) и фазы (б) коэффициента передачи по напряжению симметричного двухвходового резонатора ПАВ (материал подложки ST-срез кварца) для схемы на рис. 1.11 от частоты; при N₀ = 400, N = 22, l_p = 3,75λ, l = 48,5λ, k²_m = 0,0012: ----- ε = 0,001; - - - ε = 0,002

В заключение отметим, что отмеченные выше недостатки эквивалентных схем ЛЗ ПАВ целиком присущи и приведенным эквивалентным схемам одновходного и двухвходного резонаторов ПАВ.