2.5. Амплитудные характеристики и стабильность частоты автогенераторов

Рассмотрим амплитудно-частотные характеристики автогенераторов с несогласованными ЛЗ ПАВ или резонаторами ПАВ. Возьмем случай "мягкой" зависимости выходного тока АЭ автогенератора от амплитуды автоколебаний. Как следует из (2.42),

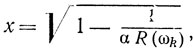
где R(ω_k) определяется из выражений (2.22) и (2.34).

Зависимости амплитуды колебаний от собственной частоты, рассчитанные по формулам (2.47), (2.22) для симметричной ЛЗ ПАВ, выполненной на HС-срезе кварца с N = 100, g = ω_аС_T и g = Gˆ, приведены на рис. 2.9. Видно, что зависимость управляющего сопротивления автогенератора от частоты приводит к существенной частотной зависимости амплитуды колебаний.

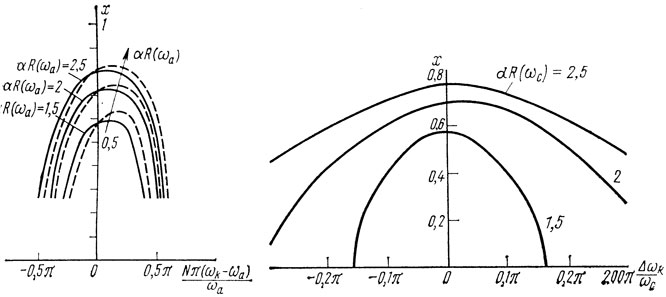
Рис. 2.9. Слева. Зависимости нормированной амплитуды колебаний от собственной частоты ω_k в автогенераторе с несогласованной симметричной ЛЗ ПАВ: ---- g = ω_aC_T; - - - g = G; N = 100, HС-срез кварца. Рис. 2.10. Справа. Зависимость нормированной амплитуды колебаний от собственной частоты для автогенератора с резонатором ПАВ (ε = 0,0025, l_р = 3,75λ, l_п = 22λ, l = 48λ, N₀ = 200)

Аналогичные зависимости для автогенератора с симметричным резонатором ПАВ приведены на рис. 2.10. Они соответствуют случаю

Приведенные расчетные зависимости для автогенератора на ЛЗ ПАВ и резонатора ПАВ качественно одинаковы. Интересно, что эти зависимости несимметричны, что объясняется несимметричностью частотной зависимости управляющего сопротивления автогенераторов на несогласованных устройствах на ПАВ.

Рассмотрим следующие мощностные характеристики автогенераторов: мощность, отдаваемую автогенератором в нагрузку (Рн), и мощности, рассеиваемые по первой гармонике в АЭ (Р_АЭ) и устройстве на ПАВ (Р_ПАВ). Выражения для определения указанных мощностей имеют вид:

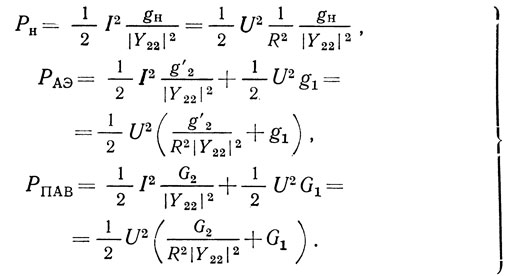
где I - амплитуда первой гармоники выходного тока АЭ; g'₂ - выходная активная проводимость АЭ; Y₂₂ - собственная проводимость входа 2-2' линейной системы автогенератора (см. рис. 2.1).

Требования, накладываемые на эти мощности, различны. Например, мощность, отдаваемую автогенератором в нагрузку, желательно увеличить, а мощность, рассеиваемую в АЭ и устройстве на ПАВ, уменьшить.

Рассмотрим вначале случай, когда основной задачей является получение максимальной мощности в нагрузке. При этом обычно стремятся полностью использовать АЭ по напряжению и току. Будем считать, что АЭ полностью используется по току. Это позволяет считать ток I в (2.48) постоянным. Тогда при изменении g_н мощность Р_н [как следует из (2.48)] будет максимальной, если выполняется условие

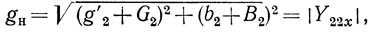
где |Y_22x| - модуль выходной проводимости линейной системы автогенератора при g_н = 0.

Для автогенераторов с ЛЗ ПАВ на частоте ω_л = ω_а это условие имеет вид

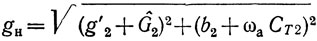
или g_н ≈ ω_kC_T2 для ЛЗ ПАВ на слабых пьезоэлектриках и АЭ, у которых выходная проводимость мала, √(g'₂)² + b²₂ << ω_аС_T2.

Для автогенераторов с резонатором ПАВ приведенное выше условие на частоте ω_k = ω_c при максимальном значении взаимной проводимости принимает вид

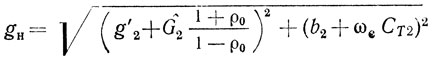
или соответственно g_н ≈ ω_сС_T2.

В этом случае

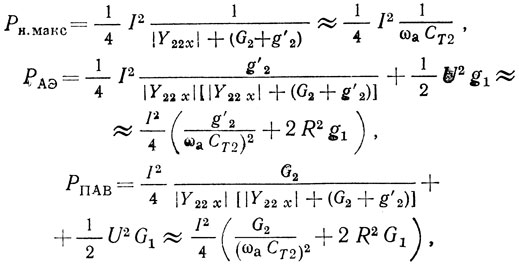
а КПД генератора

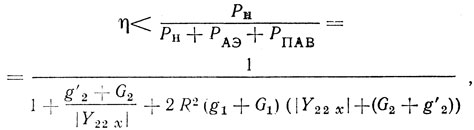
где ω_А = ω_а и G₂ = Gˆ₂ для ЛЗ АПВ; ω_А = ω_с и G₂ = Gˆ₂(1 + ρ₀)/(1 - ρ₀) для резонатора ПАВ.

Если при изменении g_н выходной ток АЭ нельзя считать постоянным, то условие, при котором Р_н достигает максимума, существенно усложняется и для "мягкой" колебательной характеристики может быть записано в следующей неявной форме:

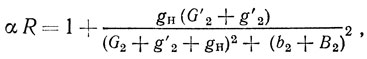
где R - управляющее сопротивление.

Из (2.51) видно, что оптимальная выходная мощность

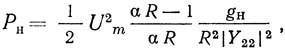
где U_m = √4α/3γ₀ достигается при 1 < αR < 2. При этом значение g_н не должно превышать g_н^кр, при котором αR = 1, а значит, и I = 0. Выражение для g_н^кр имеет вид

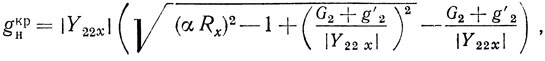
где R_x - управляющее сопротивление при холостом ходе по нагрузке.

На практике часто бывает ситуация, когда сопротивление нагрузки задано, но по-прежнему требуется получить от генератора максимальную мощность. В этом случае оптимизация Р_н достигается изменением параметров |Y₂₂| и R в выражении (2.53). Если изменяется только |Y₂₂| (а за счет изменения |Y₂₂| изменяется и R), то условием достижения максимального значения Р_н является условие максимума R. Если |Y₂₂| постоянно, а управляющее сопротивление R изменяется (например, за счет изменения |Y₁₁|), то Р_н достигает максимального значения

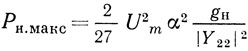
при выполнении равенства

Если αR < 3/2 во всем диапазоне изменения R, то Р_н максимально при максимуме R; если же во всем диапазоне изменения R αR > 3/2, то при максимальном значении R мощность Р_н минимальна.

Рассмотрим зависимость Р_н от собственной частоты ω_k. При изменении ω_k изменяется как |Y₂₂|, так и R (например, за счет изменения Г(ω_k). Однако наибольшее влияние при этом оказывает изменение R. Тогда из (2.55) следует, что зависимость Р_н от ω_k будет иметь один максимум на частоте, где R принимает максимальное значение, если αR_макс ≤ χ и два максимума, если αR_макс > χ. Критическое значение (αR_макс)_кр = χ близко к 3/2. Максимумы Р_н располагаются по разные стороны от частоты, где R максимально, и при увеличении αR_макс расстояние между экстремальными точками и величина провала между ними возрастают. Например, при αR_макс = 2 на скатах частотной зависимости R(ω) мощность в нагрузке будет приблизительно в 1,2 раза больше, чем там, где R принимает максимальное значение, а при αR_макс = 2,5 - 1,5 раза.

Зависимости мощности в нагрузке от собственной частоты для автогенератора с несимметричной ЛЗ ПАВ для разных величин αR(ω_a) и двух вариантов согласования выходной проводимости АЭ и ЛЗ ПАВ (g = ω_а)С_Т и g = G) приведены на рис. 2.11. Зависимости мощности, выделяемой в нагрузке, от частоты для автогенератора с симметричным резонатором ПАВ для различных значений αR(ω_c) при g₂ = ω_cC_T2 представлены на рис. 2.12.

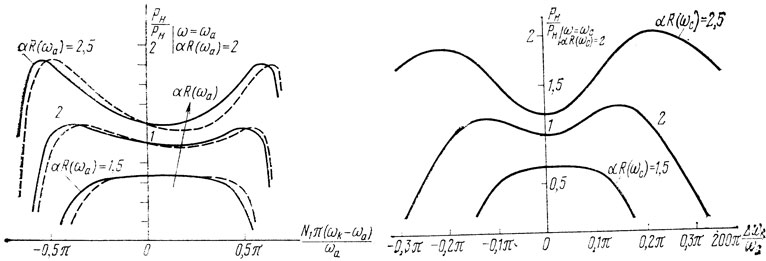
Рис. 2.11. Слева. Зависимость нормированной мощности колебаний, отдаваемой АЭ на выходе автогенератора с несимметричной несогласованной ЛЗ ПАВ от собственной частоты колебаний ----- g_i = ω_aС_Ti; - - - g_i = G_i; i = 1, 2; N₁ = 100; N₂ = 10; HС-срез кварца. Рис. 2.12. Справа. Зависимость мощности, выделяемой в нагрузке, от собственной частоты для автогенератора с резонатором ПАВ (ε = 0,0025), l_p = 3,75λ, l_п = 22λ,; l = 48λ, N₀ = 200)

Приведенные зависимости для автогенератора с ЛЗ ПАВ и автогенератора на резонаторе ПАВ аналогичны.

Исследуем нестабильность частоты в рассматриваемых автогенераторах, определяемую медленными и малыми изменениями параметров автогенератора ω_k, R, Т_э, Н, s_⊥, s_|| и s_a, s_p.

Из (2.20) в предположении, что нелинейная составляющая входного тока АЭ мала и незначительно влияет на стационарный режим автогенератора, можно получить следующее выражение для относительной нестабильности частоты для автогенератора с резонатором ПАВ

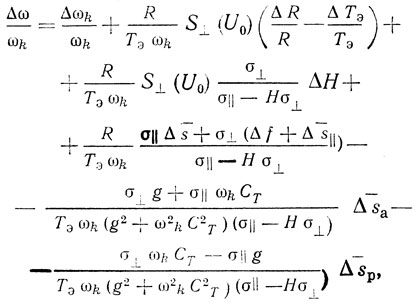
где Δω_л/ω_c - относительная нестабильность собственной частоты линейной резонансной системы автогенератора; ΔR/R - относительная нестабильность управляющего сопротивления; ΔТ_э/Т_э - относительная нестабильность эквивалентного времени задержки; ΔН - нестабильность параметра неизохронности; Δf = Δα + 1/R ΔR/R - нестабильность запаса по регенерации; Δs‾_||, Δs‾_⊥, Δs‾_a, Δs‾_p - собственные нестабильности соответствующих токовых коэффициентов АЭ;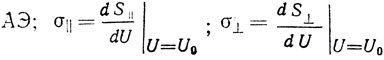  
- производные по амплитуде напряжения от синфазной и квадратурных составляющих крутизны тока АЭ в точке стационарного режима.

При выводе (2.56) из (2.20) производные по времени от U и Ψ полагались равными нулю вследствие предположения о медленности изменения параметров автогенератора. Малость же изменения параметров дала возможность линеаризовать уравнения (2.20) и окончательно представить их в виде (2.56).

Из (2.56) непосредственно получаем выражение для относительной нестабильности частоты автогенератора на ЛЗ ПАВ, если в (2.56) заменим Т_э на Т. Из (2.56) видно, что влияние нестабильности Δs‾_⊥ на нестабильность частоты тем меньше, чем меньше величина

а влияние нестабильностей Δs‾_|| + Δf тем меньше, чем меньше

Видно, что если автогенератор находится вблизи границы устойчивости σ_|| - Нσ_⊥ ≈ 0, то влияние нестабильностей Δs‾_⊥ и Δs‾_|| + Δf на нестабильность частоты существенно возрастает.

Рассмотрим наиболее простой случай, когда S_⊥(U) = 0, а фаза крутизны нелинейной составляющей выходного тока АЭ имеет нестабильность Δs‾_⊥. Тогда из (2.56) имеем для автогенератора на резонаторе ПАВ

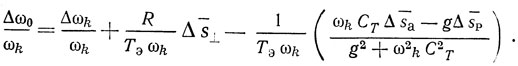
Для автогенератора с ЛЗ ПАВ в (2.57) необходимо заменить Т_э на Т.

Из (2.56) и (2.57) следует, что для повышения стабильности частоты автогенератора необходимо:

1) применять в устройствах на ПАВ стабильные пьезокристаллы, например ST-срез кварца;

2) использовать ЛЗ ПАВ с большой относительной акустической длиной;

3) применять конструкцию автогенераторов с резонаторами ПАВ, которая дала бы возможность работать с максимально возможным эквивалентным временем задержки резонатора ПАВ, например, работать на частотах вблизи ω_р = ω_с;

4) стабилизировать источники электропитания;

5) подавлять прямое прохождение в устройствах на ПАВ и применять преобразователи с такой топологией, которая обеспечивает максимальное подавление высших гармонических составляющих тока АЭ, поскольку их влияние приводит к изменению фазы крутизны выходного тока АЭ;

6) работать с возможно меньшими базовыми токами, стремясь к использованию АЭ с большим входным сопротивлением для уменьшения влияния нестабильности входных токов АЭ;

7) работать в недонапряженном режиме для улучшения гармонического состава токов АЭ.