2.4. Укороченные уравнения

Используя приведенный выше материал, нетрудно получить укороченные уравнения автогенераторов на несогласованных линиях задержки и резонаторах ПАВ. Для случая слабого прохождения ПАВ через ПАВ-устройство, а также при условии, что для ЛЗ ПАВ справедливо

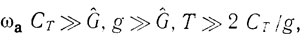
а для резонатора ПАВ

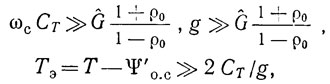
эти уравнения примут вид (2.20) с коэффициентами

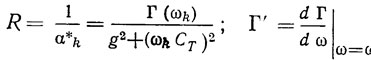
для ЛЗ АПВ Т₀ = Т (1 + Н²); H = - Г'/ГT;

для резонатора ПАВ T₀ = T_Э(1 + H²); H = - Г'/ГT_Э; T_Э = Т - Ψ_о.с;

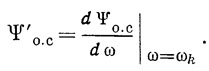
Исследуем полученные уравнения для случая, когда нелинейная составляющая входного тока АЭ равна нулю, т. е. i₁ = 0. Рассмотрим вначале случай, когда фаза крутизны АЭ не зависит от амплитуды колебаний, т. е. S_⊥ = 0. При этом амплитуда стационарных колебаний определяется из уравнения

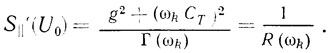
Выражение (2.35) аналогично по форме уравнению стационарных колебаний одноконтурного LC-автогенератора. Величина

является управляющим сопротивлением автогенератора. Чем больше ω_kC_T и g и меньше Г(ω_k), тем меньше R и хуже возбуждается автогенератор с ПАВ-устройством. Последнее следует из условия самовозбуждения автогенератора с устройством на ПАВ (см. рис. 2.1), которое имеет традиционный вид

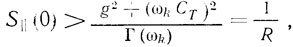
т. е. α > α^*_k или Rα > 1.

Условие устойчивости стационарного режима в предположении малого запаса по самовозбуждению выражается неравенством

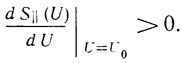
Если не ограничиваться случаем малого запаса по самовозбуждению, то, используя полное уравнение автогенератора (2.14), можно показать, что условие устойчивости стационарного режима автогенератора при ω_k = ω_a имеет вид (i₁ = 0, S_⊥ = 0):

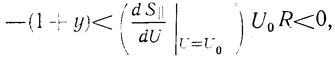
где

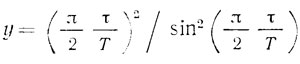
- для симметричной ЛЗ ПАВ;

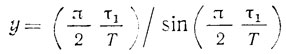
- для несимметричной ЛЗ ПАВ.

Отметим, что поскольку в несимметричной ЛЗ ПАВ Т ≥ τ₁/2, то для нее (как и для симметричной ЛЗ АПВ) справедливо y > 0.

Значение y определяется частотно-избирательными свойствами управляющего сопротивления. Срыв устойчивости стационарного режима при невыполнении условия (2.38) возникает из-за возбуждения типов колебаний, для которых набег фазы по кольцу обратной связи равен π (с точностью до 2πn, где n - натуральное число). Это объясняется тем, что при определенных амплитудах основного колебания локальная крутизна АЭ может стать отрицательной. При этом для гармонических вариаций амплитуды основного типа колебания АЭ автогенератора будет обеспечивать фазовый сдвиг, отличающийся на π от фазового сдвига в том же активном элементе для невозмущенных колебаний основного типа.

Так как спектр гармонических вариаций амплитуды основного колебания представляет две симметричные боковые частотные составляющие спектра основного колебания, то, принимая во внимание, что для упоминавшихся выше паразитных типов колебаний собственные частоты также симметрично расположены относительно собственной частоты основного типа колебания, можно понять, что при достаточно больших отрицательных dS_||/dU возможно возникновение паразитных колебаний. Они будут возникать, когда для них будет выполняться условие самовозбуждения.

Коэффициент усиления АЭ для вариаций амплитуды определяется величиной отрицательной локальной крутизны АЭ, а коэффициент передачи ЛЗ на частотах паразитных колебаний - величиной 1/y. Значит, чем меньше y, тем при меньших dS_||/dU возможно возникновение паразитных колебаний. В свою очередь, их возникновение соответствует неустойчивости одночастотного режима автогенератора.

Проиллюстрируем условие (2.38) на примере автогенератора с "мягкой" зависимостью крутизны АЭ от амплитуды автоколебаний S_|(U) = α - (3/4)γ₀U². В этом случае

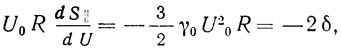
где δ = |α-α^*/α^*| - запас по самовозбуждению.

Таким образом, условие (2.38) справедливо только при δ < δ_г, где δ_г - граничный запас по самовозбуждению, равный

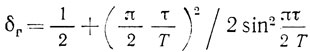
для автогенератора на симметричной ЛЗ ПАВ и

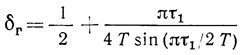
для автогенератора с несимметричной ЛЗ ПАВ.

При использовании ЛЗ ПАВ, обеспечивающей модовую селекцию (T = τ), получаем δ_г = 1,73 для симметричной ЛЗ ПАВ и δ_г = 1,29 для несимметричной. Большее значение δ_г для симметричной ЛЗ ПАВ объясняется ее большей частотной избирательностью по сравнению с несимметричной ЛЗ ПАВ при одинаковых τ и τ₁.

Если фаза крутизны выходного тока АЭ не зависит от амплитуды колебаний, т. е. если S_⊥ = 0, то, как следует из (2.34), частота стационарных автоколебаний ω₀ от амплитуды колебаний не зависит и равняется собственной частоте линейной резонансной системы ω_k. Автогенератор изохронный в стационарном режиме. Однако он может быть неизохронным в переходном режиме. Действительно, если в (2.34) Н ≠ 0, то процесс установления амплитуды колебаний сопровождается изменением мгновенной частоты, причем даже тогда, когда АЭ безынерционный.

Это имеет место, когда частота колебаний соответствует скату частотной характеристики ЛЗ ПАВ или резонатора ПАВ. Если ω_k равна частоте, на которой частотная зависимость R(ω) и при сделанных предположениях Г(ω) проходят через максимум, то параметр неизохронности Н равен нулю. Автогенератор при этом изохронный в переходном режиме и с инерционным АЭ (если: S_⊥ = 0). Зависимость параметра неизохронности Н от собственной частоты ω_k для ЛЗ ПАВ приводится на рис. 2.6, а, а для резонатора ПАВ - на рис. 2.7, а. На рис. 2.6, б и 2.7, б показаны для этих ?случаев зависимости эквивалентной постоянной времени линейной резонансной системы T₀ от частоты. Видно, что для ЛЗ ПАВ при ω_k = ω_а эквивалентная постоянная времени минимальна и равна времени задержки ПАВ в ЛЗ. При расстройке частоты ω_k от ω_а, T₀ становится больше Т и монотонно увеличивается при увеличении расстройки. При ω_k = ω_а + (2π/τ) параметры принимают бесконечно большие значения.

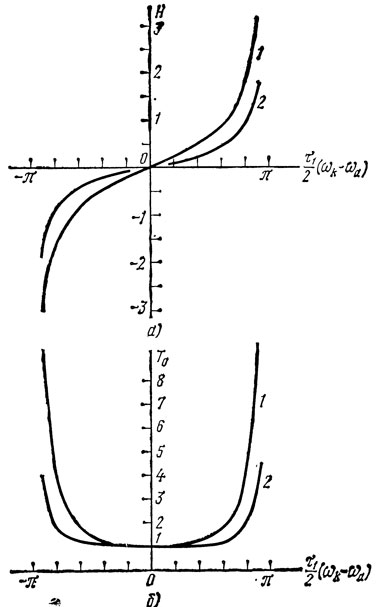
Рис. 2.6. Зависимости параметра неизохронности H (а) и эквивалентной постоянной времени линейной резонансной системы Т₀ (б) от собственной частоты ω_k для автогенератора с ЛЗ ПАВ (при Т = τ, T = τ₁, g_i >> G_i, ω_аС_Тi >> G_i, T >> 2С_Тi/g_i, i = 1, 2); 1 - симметричная ЛЗ ПАВ τ₁ = τ₂ = τ = T; 2 - несимметричная ЛЗ ПАВ τ₁ = Т

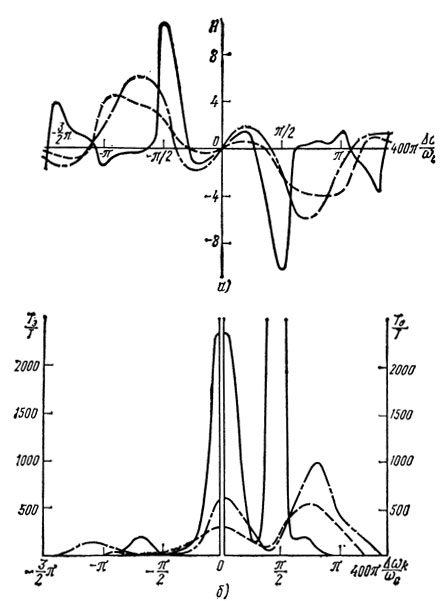
Рис. 2.7. Зависимость параметра неизохронности H (а), эквивалентной времени задержки резонатора ПАВ Т_э и эквивалентной постоянной времени линейной резонансной системы автогенератора Т₀ (б) от собственной частоты (l_р = 3,75λ, l_п = 22λ, l = 48λ): ----- N₀ = 400; ε = 0,0025; - - - N₀ = 200, ε = 0,0025; - - - ^. - - - N₀ = 200, ε = 0,005

Рассмотрим влияние зависимости фазы крутизны выходного тока АЭ от амплитуды на характеристики автогенератора. Из (2.34) получаем следующие уравнения стационарного режима для. К автогенератора с ЛЗ ПАВ:

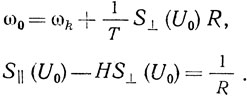
В резонаторе ПАВ в первом уравнении (2.39) вместо Т должно быть Т_э.

Таким образом, наличие зависимости фазы крутизны АЭ от амплитуды колебаний приводит к тому, что от амплитуды колебаний зависит и частота в стационарном режиме. Автогенератор с устройством на ПАВ становится неизохронным и в стационарном режиме.

Условие устойчивости стационарного режима при S_⊥ ≠ 0 имеет вид

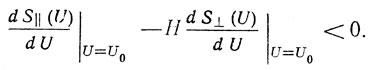
Условие самовозбуждения автогенератора остается прежним, так как S_⊥(0) = 0, и имеет вид (2.36). Это означает, что в таком генераторе можно ожидать появления жесткого режима возбуждения колебаний или прерывистой генерации даже при "мягкой" зависимости S_||(U).

Рассмотрим переходные процессы в автогенераторе с устройством ПАВ. Предположим, что S_⊥ = 0, a S_||(U) можно аппроксимировать "мягкой" зависимостью от амплитуды автоколебаний

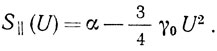
Тогда, вводя безразмерную амплитуду x = U/U_m, где U_m = √4α/3γ₀, из (2.23) получаем

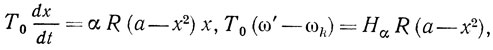
где a = 1 - (1/αR) = δ/αR - параметр регенерации; δ = [(α - α^*_k)/α^*_k] - запас по самовозбуждению; ω' = ω₀ + dΨ/dt - мгновенная частота автоколебаний.

Решение системы (2.42) имеет вид

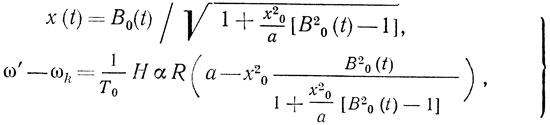
где В₀(t) = х₀ехр(δt/T₀); х₀ - начальная безразмерная амплитуда при t = 0.

Зависимости безразмерной амплитуды x(t) и относительной мгновенной частоты колебаний (ω' - ω_k)/ω_k от времени, рассчитанные по выражениям (2.43), приведены на рис. 2.8, а, б. Для конкретности были взяты следующие значения параметров: δ = 0,2 и 0,5, x₀ = 0,2√a, H = 0 и 0,5.

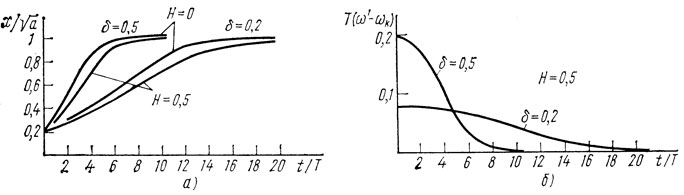
Рис. 2.8. Зависимости амплитуды (а) и частоты (б) от времени в автогенераторе с ЛЗ ПАВ при х₀ = 0,2√а

Выражения (2.43) позволяют оценить время переходного процесса по заданным установившимся значениям амплитуды и частоты:

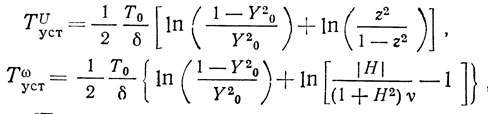
где Y₀ = (x₀/√а) - нормированная начальная амплитуда колебаний; z = x_уст/x(t → ∞) - оценка установления режима по амплитуде; ν - оценка установления режима по частоте (для ЛЗ ПАВ ν = |ω' - ω_k|T, для резонатора ПАВ ν = T_э|ω' - ω_k|).

Величина z показывает, что процесс установления амплитуды считается законченным, если относительная амплитуда принимает значение zx(t → ∞). В свою очередь, установление частоты считается законченным, если относительная разность между мгновенной и стационарной частотами достигает значения ν.

Из (2.44) видно, что при

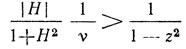
время переходного процесса будет определяться временем установления частоты.

Если оценивать время переходного процесса по времени установления амплитуды, то из (2.43) для ЛЗ ПАВ легко определить поправку на частоту в момент достижения амплитудой значения zx(t → ∞)

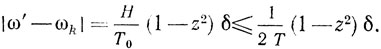
Для резонатора ПАВ необходимо в правой части (2.46) заменить Т на Т_э^мин.

Видно, что поправка на частоту максимальна при H = 1 и тем больше, чем больше δ/Т(δ/Т_э^мин). Отметим, что формулы (2.43) позволяют лишь оценить характер переходных процессов в автогенераторе с устройствами на ПАВ, особенно при запасе по самовозбуждению δ, соизмеримом с 1.

При больших запасах по самовозбуждению переходный процесс в автогенераторах с устройством на ПАВ может иметь колебательный характер или даже идти с прерывистой генерацией. Это объясняется возможностью существования в переходном режиме дополнительных типов колебаний, для которых ни в стационарном режиме, ни в режиме малых амплитуд в начале переходного режима условия существования не выполняются. Но они могут выполняться при достижении амплитудой основного колебания некоторого промежуточного значения.

Кратко это можно объяснить тем, что при данном значении амплитуды основного колебания локальная крутизна АЭ становится отрицательной, что дает возможность развиваться типам колебаний, набег фазы по цепи обратной связи для которых равен нечетному числу я. При малых амплитудах основного колебания они не возбуждаются, так как локальная крутизна при этом положительна и для них не выполняются условия фазового баланса. В стационарном же режиме они полностью подавляются доминирующим основным колебанием. Взаимодействие в переходном режиме этих дополнительных колебаний с основным и дает своеобразный режим биений или колебаний амплитуды и частоты.

Таким образом, укороченные уравнения (2.20) лишь приближенно описывают динамику работы автогенераторов с устройствами на ПАВ. В то же время, они достаточно просты, позволяют понять физику основных протекающих процессов и дать достаточно простую их аналитическую оценку. Это, например, относится к времени переходного процесса. Более точное исследование переходных процессов возможно лишь с привлечением вычислительной техники.