2.3. Автогенератор с несогласованным двухвходовым резонатором

Для упрощения анализа аналогично несогласованной ЛЗ ПАВ (см. § 2.2) рассмотрим автогенератор на симметричном двухвходовом резонаторе ПАВ. Будем считать, что входной и выходной преобразователи резонатора имеют одинаковую длину l_1п = l_2п = l_п, а расстояние от решеток до преобразователей и длина самих решеток одинаковы, т. е. l_p1 = l_p2 = l_p и N₀₁ = N₀₂ = N₀. По-прежнему будем считать, что выполняется условие слабого прохождения ПАВ через резонатор. При этом собственные частоты эквивалентной резонансной системы сон и управляющее сопротивление R автогенератора можно определить из (2.12) и (2.13). В удобной для графической иллюстрации форме уравнение (2.12) запишется в виде

Уравнение (2.26) отличается от соответствующего уравнения (2.21) для автогенератора на несогласованной ЛЗ ПАВ лишь присутствием слагаемого Ψ_o.c.

Так же, как и в (2.21), М показывает, сколько длин волн укладывается на расстоянии L между центрами преобразователей; Ψ - сдвиг фазы на входе и выходе линейной резонансной системы; Ψ = arctg {[ω_kC_T + b_a(ω_k)]/[g + G(ω_k)]}.

Выражения для определения R и α^*_k формально аналогичны соответствующим выражениям для несогласованной ЛЗ ПАВ. Понятно, что конкретные значения и частотные зависимости этих параметров для ЛЗ ПАВ и резонатора ПАВ отличаются.

Из (2.26) можно определить номер той моды колебания, частота которой близка к ω_k. Очевидно, что номер такой частоты k (как и для ЛЗ ПАВ) близок к М. Графическое решение (2.26) при различных значениях Т для симметричного резонатора ПАВ, выполненного на ST-срезе кварца с количеством отражателей в решетках N₀ = 200, коэффициентом рассогласования ε = 0,005 и ε = 0,0025 при g = ω_аС_T, приводится на рис. 2.5, а. На рис. 2.5, б приводится зависимость управляющего сопротивления от Δω_k - расстройки собственной частоты ω_k относительно центральной частоты отражения ω_c.

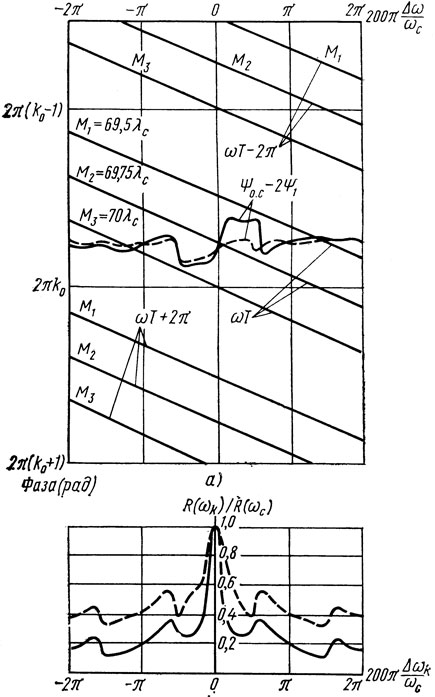
Рис. 2.5. Графическое решение уравнения баланса фаз для автогенератора с резонатором ПАВ (а) и зависимость его управляющего сопротивления от собственной частоты (б) (φ = 0, g = ω_cC_T, N₀ = 200, ST-срез кварца; l_p = 3,75λ, l_п = 22λ, l/λ = 48, 47, 75, 47,5): ----- ε = 0,005; - - - ε = 0,0025

Из сравнения рис. 2.5 и рис. 2.3 следует, что анализ автогенератора с резонатором ПАВ более сложен, чем автогенератора с ЛЗ ПАВ. Это объясняется существенной частотной зависимостью Ψ_о.с(ω), которая в случае ЛЗ ПАВ отсутствует.

Определим условия одномодовой генерации для рассматриваемого автогенератора при условиях, что собственная частота линейной резонансной системы ω_k совпадает с центральной частотой отражения решетки ω_c, а ширина главного лепестка частотной зависимости резонатора ПАВ определяется главным лепестком зависимости коэффициента отражения решетки от частоты.

Последнее предположение означает, что

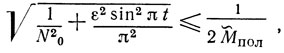
где

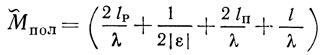
является полной акустической длиной резонатора с учетом проникновения ПАВ в отражательную решетку на глубину λ/4|ε|.

Расстояние между частотой основной моды колебания ω_k = ω_k и моды, ближайшей к ней ω_k+1, определим из равенства

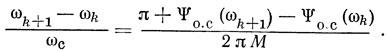
Для упрощения вывода (2.28) предполагалось, что φ и Ψ в пределах полосы отражения решеток резонатора ПАВ от частоты не зависят.

Если ω_k = ω_c и модуль |Y₁₂| = Г принимает максимальное значение, то Ψ_о.с(ω_k) = 0. Очевидно, что для одномодовой генерации желательно получить такие значения частот соседних с основной модой колебаний, которые будут приходиться на нули частотной зависимости коэффициента отражения или близкие к ним области. При этом, как следует из (2.4), Ψ_о.с (ω_k+1) = 0.

Нули коэффициента отражения решеток приблизительно соответствуют минимальным значениям управляющего сопротивления автогенератора на рис. 2.1, которые в отличие от случая ЛЗ ПАВ отличны от нуля. Это объясняется следующим. Если коэффициент отражения решеток резонатора ПАВ на какой-то частоте равен нулю, то на этой частоте резонатор ПАВ работает как обычная линия задержки ПАВ. Однако для этой ЛЗ ПАВ коэффициент передачи, который и будет в нашем случае определять минимальное значение R резонатора ПАВ, совсем не обязательно должен быть равен нулю.

Из сказанного следует, что условие одномодовой генерации будет выполняться, если

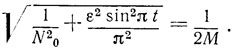
Понятно, что оно будет выполняться и при условии

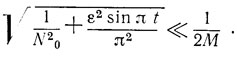
В первом случае соседние собственные частоты попадают на нули главного лепестка частотной зависимости коэффициента отражения, а во втором они приходятся на боковые лепестки частотной зависимости коэффициента отражения с большими порядковыми номерами. Отметим, что при выполнении (2.27) автоматически выполняется и (2.30), поскольку

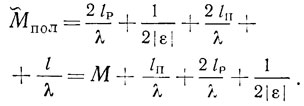
Определим относительную акустическую длину между центрами преобразователей резонатора ПАВ, при которой обеспечивается ω_k = ω_c. Из (2.26) получаем

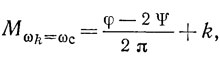
где k = 0, 1, 2, ...

Отсутствие в (2.31) Ψ_o.c объясняется предположением о том, что ω_k = ω_c. При этом Ψ_о.с = 0.

Таким образом, чтобы автогенератор работал в одночастотном режиме, необходимо выполнение условия однорезонансности характеристики резонатора ПАВ (2.27) и условия оптимальной акустической длины М_oпт между центрами преобразователей (2.31). Например, если φ = 0, то из (2.31) для слабых пьезоэлектриков в предположении, что выходная и входная проводимости АЭ согласованы, т. е. равны по модулю проводимостям, обусловленным статическими емкостями преобразователей (ωC_Ti = g_i, i = 1, 2), величина M_опт равна

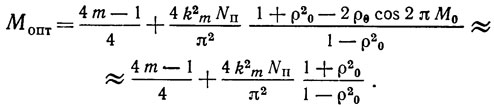
При выводе (2.32) предполагалось, что φ = 0 и

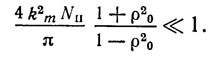
Из (2.32) видно, что в рассматриваемом случае относительная акустическая длина резонатора ПАВ близка к длине, равной нечетному количеству четвертей длины волны на частоте ω_c. Например, для резонатора ПАВ, выполненном на ST-срезе кварца с N_п = 22 и ρ₀ = 0,9, из (2.32) получаем

Отметим, что оптимизация параметра М_опт для автогенераторов с несогласованным резонатором ПАВ существенно сложнее, чем для автогенераторов с несогласованной ЛЗ ПАВ. Это объясняется тем, что при изменении расстояния между центрами преобразователей изменяется и акустическая длина резонансной полости резонатора. Последнее приводит к изменению его резонансной частоты, т. е. к ее расстройке относительно частоты ω_c. Таким образом, оптимизация расстояния L_p должна сопровождаться таким изменением l_р, при котором ω_p = ω_c. Последнее достигается при l_p/2 + N_п/2 = n-2M/4, где n - натуральное число. Однако при этом центры ВПШ могут не располагаться в пучности стоячей волны. Это уменьшает Г(ω_c), а значит и управляющее сопротивление.