2.2. Автогенератор на несогласованной линии задержки ПАВ

Как отмечалось, важным достоинством автогенераторов на устройствах на ПАВ является то, что они могут быть выполнены в микроэлектронном исполнении. Наиболее просто это достигается при отказе от дополнительных индуктивных элементов, подключаемых ко входу и выходу ЛЗ ПАВ или двухвходового резонатора ПАВ для компенсации статических емкостей преобразователей, и объясняется известными сложностями, встречающимися в производстве индуктивных элементов в пленочных микросхемах. Отказ от компенсирующих индуктивностей сопровождается существенным снижением коэффициентов передачи устройства на ПАВ по напряжению и току, что в конечном счете ведет к необходимости большего усиления в активном звене автогенератора. Частота устройства на ПАВ без компенсирующих индуктивностей называют несогласованными устройствами на ПАВ.

Исследуем автогенератор с несогласованной ЛЗ ПАВ. В литературе встречаются описания автогенераторов как с симметричной, так и несимметричной: линиями задержки. Рассмотрим вначале автогенератор с симметричной ЛЗ ПАВ, у которой входной и выходной преобразователи имеют одинаковую длину l₁ = l₂ = l и при распространении вдоль преобразователей ПАВ задерживается на одно и то же время т. Для простоты положим, что входная и выходная проводимости АЭ с учетом нагрузки равны и чисто активны: g₁ = g₂ = g. Реактивные составляющие входной и выходной (с учетом нагрузки) проводимостей АЭ могут быть учтены соответствующим изменением статических емкостей преобразователей ЛЗ ПАВ.

Обычно для получения высокой долговременной и средневременной стабильности частоты автогенераторов линии задержки и резонаторы ПАВ делают из пьезокварца, который является слабым пьезоэлектриком. Это приводит к тому, что условия слабого прохождения ПАВ через ЛЗ и резонатор ПАВ (2.10) достаточно хорошо выполняются. Например, для ЛЗ ПАВ, выполненной на HС-срезе кварца, имеющем наибольший для различных срезов кварца коэффициент электромеханической связи k²_m = 0,0024, при числе пар электродов в ВШП N = 100, получаем

В реальной системе произведение |K_U¹²| |K_U²¹| еще меньше из-за влияния входной и выходной проводимостей АЭ, а также наличия потерь при прохождении ПАВ от одного ВШП к другому. Указанное обстоятельство позволяет определять собственные частоты он линейной резонансной системы автогенератора и критическое значение крутизны линейной части активного элемента α^*_k. из уравнения баланса фаз (2.12) и амплитуд (2.13). Запишем (2.12) в удобном для графической иллюстрации виде:

Здесь M = (L/λ) - количество длин волн, укладывающихся на длине L (расстояние между центрами преобразователей) на частоте акустоэлектрического синхронизма ω_a; Ψ = arctg ω_kC_T + b_a(ω_k) / g + G_a(ω_k) - сдвиг фазы на входе (выходе) линейной резонансной системы;

G_a = Gˆ (sin x / x)² и b_a = Gˆ sin2x-2x/2x² - активная и реактивная составляющие проводимости излучения преобразователеля ЛЗ ПАВ; x = πN(ω_k - ω_a / ω_a; φ - фаза крутизны линейной части АЭ; k = 1, 2, ... - номер моды колебания.

Выражение для определения α_k (критическое значение крутизны линейной части АЭ, при котором эквивалентное затухание в линейной резонансной системе автогенератора на частоте ω_k равно нулю) получается из уравнения баланса амплитуд (2.13) и имеет вид

Как следует из (2.22), α^*_k. принимает минимальное значение, a R = 1/α^*_k (управляющее сопротивление) - максимальное значение на той собственной частоте ω_k, которая попадает в главный лепесток частотной характеристики ЛЗ ПАВ, причем экстремальные значения α^*_k и R достигают на частоте ω_k вблизи частоты ω_a.

Проанализируем уравнения (2.21) и (2.22). Из (2.21) можно определить номер той моды колебания, частота которой наиболее близка к частоте ω_a. Видно, что номер такой моды k₀ близок к М - относительной акустической длине линии задержки ПАВ.

Для наглядности дальнейшее исследование проведем графически, используя уравнение баланса фаз (2.21). Решение этого уравнения при различных значениях Т (время задержки ЛЗ) для автогенератора с симметричной ЛЗ ПАВ, выполненной на HG-срезе кварца, при N = 100, φ = 0, g = G представлено на рис. 2.3, а. Здесь для разных мод колебаний изображены частотные зависимости сдвига фазы сигнала, которую он приобретает, проходя через АЭ с входа на выход φ - 2Ψ, а также прямая частотной зависимости сдвига фазы сигнала из-за задержки в ЛЗ ПАВ ωТ. Собственные частоты резонансной системы ω_k соответствуют точкам пересечения кривых φ - 2Ψ + 2πk и прямой ωТ. Кроме того, на рис. 2.3, б показана зависимость управляющего сопротивления R от собственной частоты ω_k.

Как видно из рис. 2.3, а, б для одномодовой генерации желательно обеспечить задержку T, близкую к τ. Однако при этом преобразователи в симметричной ЛЗ ПАВ располагаются очень близко друг к другу из-за чего сильно возрастает проходная емкость между ними и существенно усиливается эффект прямого прохождения сигнала со входа на вход ЛЗ ПАВ. Это приводит к ухудшению характеристик автогенератора.

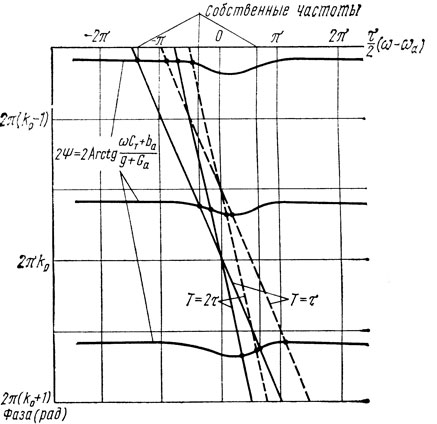
Рис. 2.3. Графическое решение уравнения баланса фаз (а) и зависимость управляющего сопротивления от собственной частоты ω_k (б) для автогенератора с симметричной несогласованной ЛЗ ПАВ (HС-срез кварца) при φ = 0, N = 100, g = G: ----- M = k₀; - - - M = k₀ - 1/2

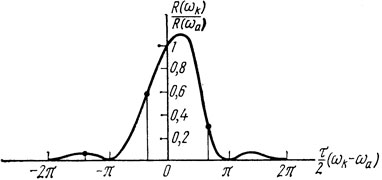
Рис. 2.3. Графическое решение уравнения баланса фаз (а) и зависимость управляющего сопротивления от собственной частоты ω_k (б) для автогенератора с симметричной несогласованной ЛЗ ПАВ (HС-срез кварца) при φ = 0, N = 100, g = G: ----- M = k₀; - - - M = k₀ - 1/2

Обеспечить T = τ и даже T > τ можно в несимметричной ЛЗ ПАВ, где имеется широкополосный преобразователь с небольшим количеством пар штырей и избирательный преобразователь длиной l₁ с большим количеством пар штырей. Поскольку частотная характеристика ЛЗ ПАВ будет в основном определяться избирательным преобразователем, то τ будет определяться задержкой сигнала в избирательном преобразователе τ₁ = l₁/V. Зависимость управляющего сопротивления от собственной частоты также определяется в основном частотной характеристикой избирательного преобразователя и будет в пределах полосы пропускания неизбирательного преобразователя близка к функции sin x/x, а не (sin x/x)², как было для симметричной ЛЗ ПАВ.

Графическое решение уравнения баланса фаз (2.12) для автогенератора с несимметричной ЛЗ ПАВ, выполненной на HС-срезе кварца с числом пар штырей в избирательном преобразователе N_изб = 100 и в неизбирательном преобразователе N_неизб = 10 при φ = 0 приводится на рис. 2.4, а. Рассматривается случай, когда входная и выходная проводимости АЭ равны проводимостям, обусловленным статистическими емкостями преобразователей g₁ = ω_aC_T1, g₂ = ω_aC_T2. На рис. 2.4, б показана зависимость управляющего сопротивления автогенератора R от собственной частоты ω_k, определяемая из выражения

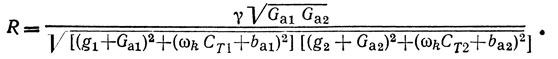
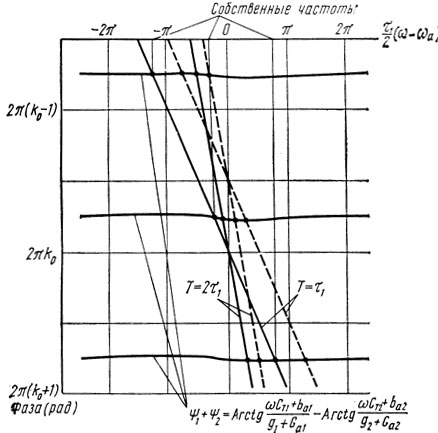
Рис. 2.4. Графическое решение уравнения баланса фаз (а) и зависимость управляющего сопротивления от собственной частоты ω_k (б) для автогенератора с несимметричной несогласованной ЛЗ ПАВ (НС-срез кварца) при φ = 0, N₁ = 100, N₂ = 10, g_i = ω_aC_Ti, i = 1, 2: ----- M = k₀; - - - M = k₀ - 1/2

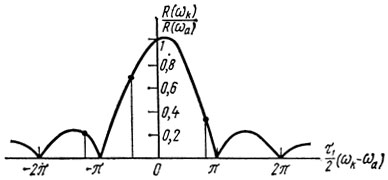
Рис. 2.4. Графическое решение уравнения баланса фаз (а) и зависимость управляющего сопротивления от собственной частоты ω_k (б) для автогенератора с несимметричной несогласованной ЛЗ ПАВ (НС-срез кварца) при φ = 0, N₁ = 100, N₂ = 10, g_i = ω_aC_Ti, i = 1, 2: ----- M = k₀; - - - M = k₀ - 1/2

Из приведенного выражения следует, что при изменении G_i величина R принимает максимальное значение, когда выполняется условие

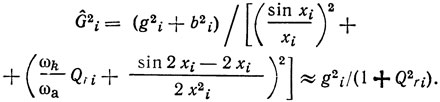
Приближенное равенство переходит в точное при ω_k = ω_a и b_i = 0. В этом случае управляющее сопротивление принимает максимальное значение, равное

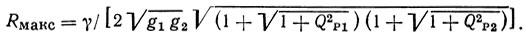
Для слабых пьезоматериалов при Q_pi >> 1 соответственно получаем G_iQ_ri = ω_аС_Тi = g_i и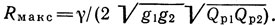  

Таким образом, как следует из рис. 2.3 - 2.4, при T, близкой к τ или τ₁ и моде колебания, частота коброй близка к частоте акустоэлектрического синхронизма ω_а, соседние моды будут подавляться, поскольку им соответствуют области нулевых или близких к ним значений управляющего сопротивления R. Для получения ω_k, обеспечивающего максимальное значение R, необходимо правильно выбирать акустическую длину ЛЗ ПАВ. Из рис. 2.3 - 2.4 видно, что изменением L ≈ l или L ≈ l_i в небольших пределах всегда можно получить требуемую собственную частоту линейной резонансной системы автогенератора ω_k, например, равную ω_a. Оптимальное значение относительной акустической длины M₀ = L/λ, при которой в одночастотном режиме частота ω_k равна частоте акустоэлектрического синхронизма ω_a, определяется из выражения

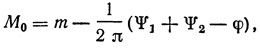
где m - натуральное число.

Если φ = 0, то из (2.23) для слабых пьезоэлектриков в предположении, что активные проводимости преобразователей соизмеримы с входной и выходной проводимостями АЭ, и при выполнении неравенства

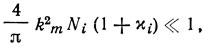
где χ_i = g_i/G_i - параметр согласования, получаем следующее приближенное выражение для определения М₀:

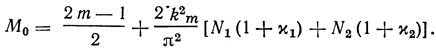
Из (2.24) видно, что оптимальная акустическая длина близка к нечетному числу половин длин ПАВ на частоте ω_а.

Если входная и выходная проводимости АЭ равны по модулю соответствующим проводимостям, обусловленным статистическими емкостями преобразователей (g_i = ω_аС_Ti), имеем

При выводе (2.25) предполагалось, что φ = 0 и 4k²_mN_i << π. Видно, что оптимальная относительная акустическая длина ЛЗ ПАВ близка теперь к нечетному числу четвертей длины волны на частоте ω_а.