2.1. Общий анализ автогенераторов

В качестве исходной рассмотрим схему автогенератора, изображенную на рис. 2.1. Следуя [43, 77, 78], выделим в ней линейную и нелинейную части. Линейная часть включает в себя ЛЗ ПАВ или двухвходовый резонатор ПАВ, нагрузку g_H и возможные цепи согласования АЭ с нагрузкой и устройством па ПАВ (индуктивности L₁ и L₂). Кроме того, для удобства описания автоколебательной системы к 1ней отнесем и линейную часть АЭ. К нелинейной части отнесем то, что определяет нелинейные составляющие входного и выходного токов АЭ. На рис. 2.1 они представлены источниками токов i₁ и i₂ соответственно, которые считаются зависящими только от входного напряжения АЭ u₁. Это справедливо, если АЭ работает в недонапряженном режиме, который является типовым для cхем стабильных автогенераторов.

Разобьем линейную часть схемы автогенератора на рис. 2.1 на два линейных четырехполюсника. К первому отнесем линейную часть АЭ, нагрузку и возможные цепи согласования АЭ с устройством на ПАВ и нагрузкой. В линейную часть АЭ кроме входной y₁ и выходной y₂ линейных проводимостей транзистора входит источник тока i₂₂(u₁) = α→u₁/i (здесь α→ - комплексная крутизна линейной части АЭ). Указанный четырехполюсник в предположении отсутствия обратного прохождения сигнала в АЭ будем описывать следующей системой уравнений в Y-параметрах:

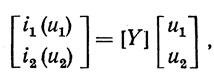
где

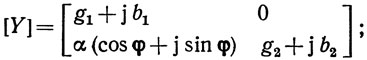
g_i, b_i - активная и реактивная составляющие собственной проводимости иго входа линейной части автогенератора без цепи обратной связи, т. е. в данном случае без устройства на ПАВ; i = 1, 2, α = √α²_а + α²_р и φ = arctg(α_p/α_a) - крутизна и фаза комплексной крутизны линейной части АЭ; α_а, α_р - активная и реактивная составляющие крутизны линейной части АЭ; α¯ = α_a + jα_p.

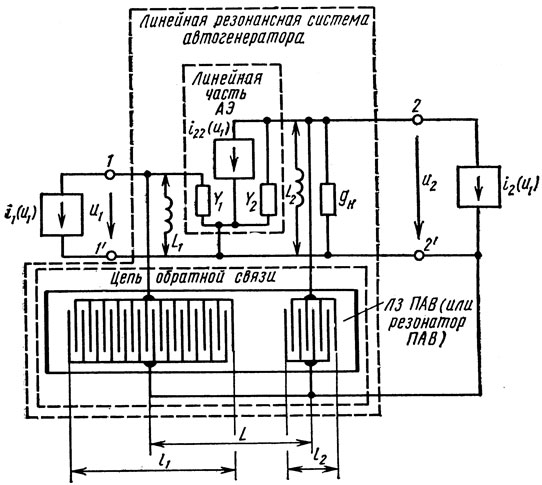
Рис. 2.1. Схема автогенератора с двухвходовым резонатором ПАВ или ЛЗ ПАВ

Второй четырехполюсник, входящий в линейную часть автогенератора, является четырехполюсником обратной связи и включает в себя лишь устройство на ПАВ. (Здесь и далее под устройством ПАВ будем понимать ЛЗ ПАВ или резонатор ПАВ.) Четырехполюсник обратной связи характеризуется матрицей Y-параметров, которую, основываясь на материале гл. 1, можно представить в следующем виде:

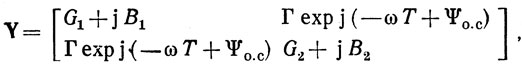
где G_i и B_i - активная и реактивная составляющие входной проводимости i-го входа устройства на ПАВ при коротком замыкании на его вторам, j-м входе; Г и Ψ_о.с являются модулем и фазой ("о! без учета чистой задержки между преобразователями Т) взаимной проводимости устройства на ПАВ.

Используя материал гл. 1, нетрудно показать, что для ЛЗ ПАВ справедливы следующие соотношения, определяющие значения элементов матрицы (2.2):

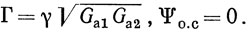
Для двухвходового резонатора ПАВ соответственно имеем (см. § 1.8):

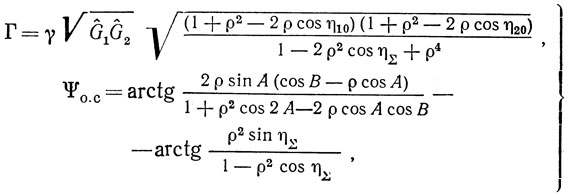
где

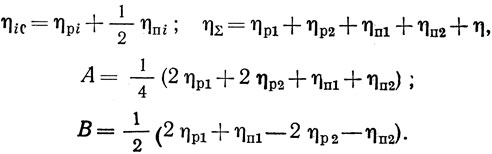
Покажем, что выделенная линейная часть схемы автогенератора на рис. 2.1 может при определенных условиях являться резонансной системой. Исследуемая автоколебательная система описывается следующей системой нелинейных уравнений:

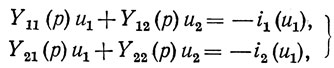
где Y_ik - элементы матрицы взаимных и собственных проводимостей линейной части автогенератора, записанной относительно входов с напряжениями u₁ и u₂ и равной сумме матриц (2.1) и (2.2); i = 1, 2; k = 1, 2; р = d/dt = jω - дифференциальный оператор.

Линейную часть автогенератора описывает система уравнений, получаемая из (2.5) подстановкой i₁ = 0, i₂ = 0. Такая система имеет ненулевое решение u, если ее определитель равен нулю. Из этого условия получим следующее характеристическое уравнение:

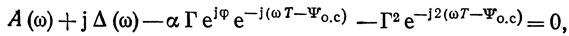
где

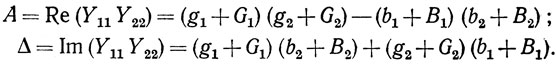
Решением (корнем) (2.6) в общем случае является некоторая комплексная частота (или частоты) ω¯_k = ω_k - jσ_k, где σ_k характеризует затухание (или нарастание) колебательного процесса на частоте ω_k. Рассмотрим случай, когда потери в диссипативных элементах линейной схемы компенсируются усилением линейной части активного элемента. Это соответствует тому, что σ_k = 0, и означает, что линейная часть автогенератора эквивалентна резонансной системе с собственной частотой ω_k и бесконечной добротностью.

Из (2.6) легко получить систему уравнений для определения собственных частот линейной резонансной системы ω_k и крутизны линейной части АЭ α^*_k, при которых потери в линейной части автогенератора полностью компенсируются внесением энергии со стороны АЭ:

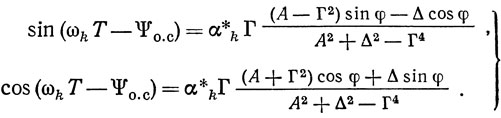
Из (2.7) получаем искомые величины

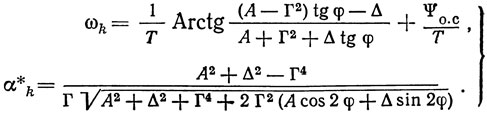
Уравнение (2.6) может быть решено относительно

в неявном виде. В этом случае

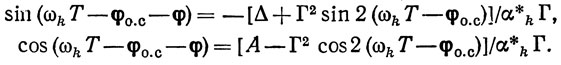
Отсюда получаем

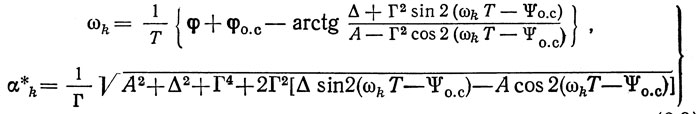
Выражения (2.8) и (2.9) эквивалентны, но в ряде случаев более удобными оказываются последние. В дальнейшем будем использовать выражения ω_k и α^*_k как в форме (2.8), так и в форме (2.9).

Уравнения (2.8) и (2.9) учитывают влияние преобразователей устройства на ПАВ друг на друга через находящийся между ними акустический звукопровод. Часто таким (влиянием можно пренебречь и рассматривать так называемый случай слабого прохождения акустических волн через устройство на ПАВ. Условие слабого прохождения имеет вид

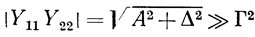
и может быть преобразовано в неравенство

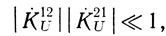
где |K¹²_U| и |K²¹_U| - модули коэффициентов передача по напряжению с первого входа на второй вход устройства на ПАВ при подключении на второй вход проводимости g₂ + jb₂ и со второго входа на первый при подключении к первому входу проводимости g₁ + jb₁.

Физически условие (2.10) говорит о том, что можно пренебречь влиянием реакции одного из входов устройства на ПАВ на режим работы другого. Иными словами, считается, что если ВШП одного из входов возбудил акустическую волну, которая вызвала электрический отклик на ВШП второго входа устройства на ПАВ, то уже этот отклик никакого влияния на режим первого входа не оказывает.

Если выполняется условие (2.10), то характеристическое уравнение (2.7) можно записать в виде

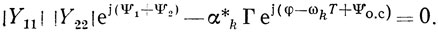
Выражения (2.8) и (2.9) при этом переходят в соотношения

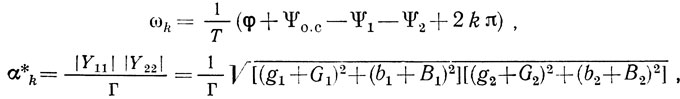
где

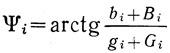
- фазовый сдвиг на i-м входе линейной резонансной системы автогенератора; i = 1, 2; k = 0, 1, 2... - номер моды колебания.

Из (2.8), (2.9) и (2.12) видно, что наличие существенной задержки сигнала в четырехполюснике обратной связи, как и для традиционных автоколебательных систем с задержкой [48-75], приводит к появлению сетки собственных частот эквивалентной резонансной системы автогенератора.

Реальный автогенератор является нелинейной системой, описываемой уравнениями (2.5). Решая их относительно входного напряжения автогенератора u₁, получим аналогично [76-79] операторное уравнение исследуемого автогенератора

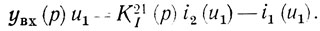
В этом уравнении y_вх = (det[Y]/A₁₁ является входной проводимостью линейной части автогенератора относительно точек 1-1'; K²¹_I = A₂₁/A₁₁ - коэффициент передачи по току со второго входа линейной части системы на рис. 2.1 на первый при коротком замыкании на первом входе; А₂₁ и A₁₁ - алгебраические дополнения элементов Y₂₁ и Y₁₁ матрицы Y-параметров линейной части автогенератора.

Для автогенераторов с устройствами на ПАВ y_вх(р) является сложной функцией частоты даже в пределах главного лепестка частотной характеристики ЛЗ ПАВ или резонатора ПАВ. Поэтому для упрощения дальнейшего анализа будем считать, что запас по самовозбуждению мал. Это позволяет предполагать, что автоколебания будут происходить на частотах, близких к собственным частотам ω_k эквивалентной резонансной системы автогенератора на рис. 2.1, а их полоса при этом будет существенно меньше полосы пропускания устройства на ПАВ. Тогда область частот, в которой необходимо учитывать изменение y_вх(jω) невелика, и последнюю вблизи сои (можно заменить разложением в ряд по малой частотной расстройке ω-ω_k и малому запасу по самовозбуждению δ = (α - α^*_k)/α^*_k, ограничившись в первом приближении линейными членами разложения

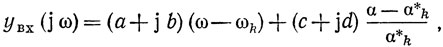
где а, b, с, d - действительные коэффициенты разложения в точке p = jω_k:

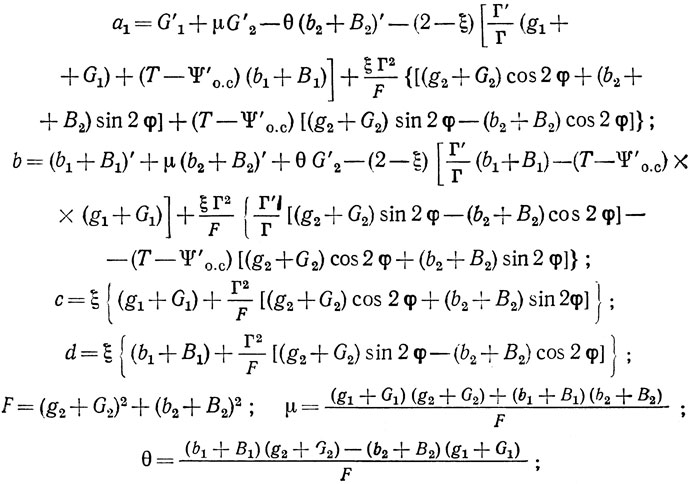
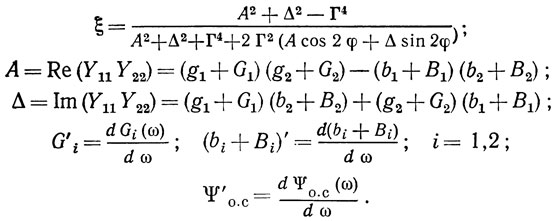
Коэффициенты а и b равны крутизнам по частоте активной и реактивной составляющих входной проводимости линейной резонансной системы автогенератора (рис. 2.1) относительно входа 1-1' на частоте ω_k при α = α^*_k; коэффициенты c и d равны активной и реактивной составляющим входной проводимости устройства на ПАВ относительно входа 1-1' при подключении к нему входной g₁ + jb₁ и выходной g₂ + jb₂ проводимостей линейной части АЭ.

Коэффициенты μ и θ учитывают возможную несимметрию линейной резонансной системы автогенератора относительно ее входов. Если система симметрична, т. е. Y₁₁ = Y₂₂, то μ = 1, θ = 0.

Величины G'_i и (b_i + B_i)' учитывают частотную зависимость активной и реактивной составляющих собственных проводимостей линейной резонансной системы; Г'/Г - относительная крутизна частотной зависимости модуля и (Т - Ψ'_o.c) - крутизна фазы элемента взаимной проводимости Y₁₂ матрицы Y-параметров устройства на ПАВ на частоте ω_k; Г'/Г и (Т - Ψ'_о.с) учитывают в первом приближении частотную зависимость модуля и фазы Y₁₂ вблизи собственной частоты ω_k.

Из (2.15) видно, что на частоте ω_k при условии, что крутизна линейной части АЭ равна α^*_k, входная проводимость линейной резонансной системы относительно точек 1-1' равна нулю. При расстройке частоты ω от ω_k даже в первом приближении изменяется не только реактивная составляющая входной проводимости резонансной системы, но и ее активная составляющая. Этим акустоэлектронный автогенератор отличается от традиционных изохронных LC-автогенераторов, в которых в указанной полосе частот активная составляющая входной проводимости в первом приближении не зависит от частоты.

Нас интересует случай, когда колебания в автогенераторе близки к гармоническим. Поэтому решение уравнений (2.14) автогенератора будем искать в виде

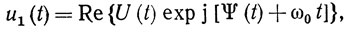
где ω₀ - частота стационарных автоколебаний, близкая к ω_k, - k-й собственной частоте линейной резонансной системы; U(t) и Ψ(t) - медленно меняющиеся амплитуда и фаза входного напряжения автогенератора.

То, что функции U(t), Ψ(t) являются медленно меняющимися функциями времени, говорит о том, что процесс u₁(t) является узкополосным. Тогда в спектре нелинейных токов активного элемента важны лишь те частотные составляющие, которые попадают в полосу частот процесса (2.16). Это дает возможность записать выражение для входного тока АЭ в виде

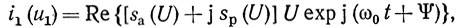
где s_a и s_p - активная и реактивная составляющие крутизны нелинейной части входного тока АЭ по первой гармонике.

Часть входного тока, характеризуемого крутизной s_a, является синфазной с входным напряжением АЭ; соответственно часть входного тока, характеризуемого крутизной s_p, сдвинута по фазе на 90° относительно входного напряжения АЭ.

Полный выходной ток АЭ i₂^п(u₁), равный сумме линейной и нелинейной составляющих, и его нелинейную составляющую i₂(u₁) для упрощения записи конечных результатов представим в виде

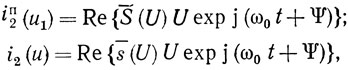
где S¯ = (S_|| + jS_⊥) exp jφ и s¯ = (s_|| + js_⊥) exp jφ - комплексные крутизны выходного тока АЭ i₂^п(u₁) и его нелинейной составляющей i₂(u₁) по первой гармонике; S_|| = α + s_|| и S_⊥ = s_⊥ - синфазная и квадратурная с комплексной крутизной линейной части АЭ α‾ = α_a + jα_p составляющие комплексной крутизны S‾ выходного тока АЭ i₂^п; s_|| и s_⊥ - синфазная и квадратурная составляющие комплексной крутизны s‾ нелинейной составляющей выходного тока АЭ i₂; α = √α²_a + α²_p и φ = arctg (α_p/α_a) - крутизна и фаза комплексной крутизны линейной части АЭ, α_а и α_р - активная и реактивная составляющие комплексной крутизны линейной части АЭ.

Представление i₂^п(u₁) и i₂(u₁) в виде (2.18) иллюстрируется на рис. 2.2, где в векторной форме изображены комплексные крутизны S‾, s‾, α‾ и их составляющие.

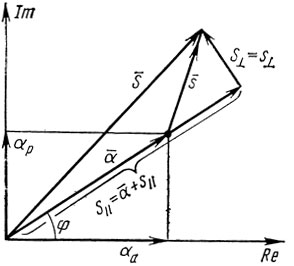
Рис. 2.2. К представлению выходного тока активного элемента в виде (2.18)

Составляющая S_⊥ = s_⊥ в (2.18) учитывает зависимость фазы крутизны выходного тока АЭ от амплитуды автоколебаний. Если S_⊥ = s_⊥ = 0 то фаза крутизны АЭ от амплитуды U не зависит и равна φ. Токи i₂^п и i₂ при этом синфазны с током линейной части АЭ.

Поскольку представление y_вх(jω) в виде (2.15) справедливо лишь в предположении малого запаса по самовозбуждению, т. е. при |α - α^*_k| << α^*_k, то и относительно величин s_a и s_p, s_|| и s_⊥ следует предположить, что они не превышают по порядку величину |α - α^*_k|. Иными словами, мы предполагаем, что нелинейные составляющие токов автоколебательной системы на рис. 2.1 настолько малы, что полоса возможных автоколебаний (в том числе и в переходном режиме) оказывается существенно меньше полосы пропускания устройства ПАВ.

Подставляя в (2.14) выражения (2.15) - (2.18) с учетом того, что в рассматриваемой полосе частот можно считать

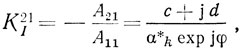
получаем аналогично [43, 76-78] следующие укороченные уравнения:

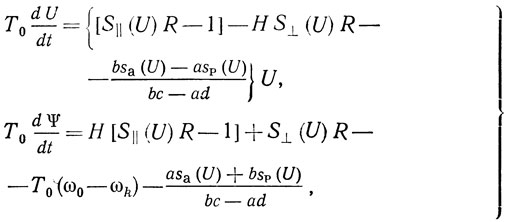
где

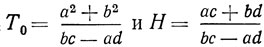
- эквивалентная постоянная времени и параметр неизохронности линейной резонансной системы; S_||(U) = α + s_||(U) - составляющая крутизны полного выходного тока АЭ по первой гармонике, синфазная с крутизной линейной части АЭ; S_⊥(U) = s_⊥(U) - составляющая крутизны полного выходного тока АЭ по первой гармонике, квадратурная с крутизной линейной части АЭ; R = 1/α^*_k - управляющее сопротивление.

Слагаемые, определяемые величинами s_a(U), s_p(U) в (2.20) возникают за счет наличия входного тока АЭ.

Рассмотрим производные по частоте от управляющего сопротивления R = 1/α^*_k где α^*_k определяется выражением (2.9), и фазовой характеристики автогенератора

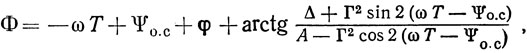
равной сдвигу фазы сигнала при его прохождении по кольцу, т. е. со входа 1-1' АЭ на его выход 2-2' и далее через устройство на ПАВ снова на вход 1-1', взятые на частоте ω_k. Из (2.9) с учетом (2.7) и (2.15) можно записать

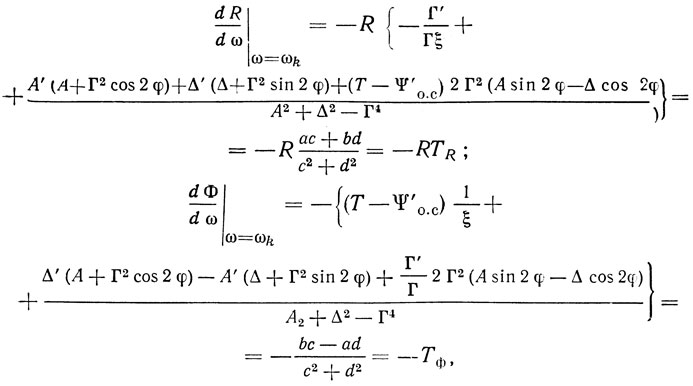
где

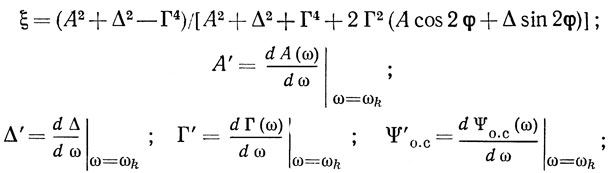
T_R и T_ф - относительная крутизна управляющего сопротивления и крутизна фазовой характеристики автогенератора.

Из полученных выражений видно, что параметр неизохронности Н и эквивалентная постоянная времени линейной резонансной системы Т₀ связаны с крутизной фазовой характеристики автогенератора T_ф = - dФ/dω и относительной крутизной его управляющего сопротивления T_R = - ¹/_R - ^dR/_dω следующим образом:

Из (2.20) видно, что внешне уравнения для автогенератора на ЛЗ ПАВ и для автогенератора на резонаторе ПАВ одинаковы с точностью до значений коэффициентов этих уравнений. Видно, что полученные уравнения даже для случая малого запаса по самовозбуждению отличаются от укороченных уравнений традиционных одноконтурных изохронных LC-генераторов, во многом напоминая уравнения RС-генераторов [76].

Укороченные уравнения одноконтурных изохронных LC-генераторов являются частным случаем уравнений (2.20). Например, для автогенератора с безынерционным АЭ и высокодобротным резонатором справедливы уравнения (2.20), в которых H = 0, a = d = 0.

Как следует из (2.20), частота автоколебаний в общем случае зависит от амплитуды колебаний, т. е. автогенератор является неизохронным.

Неизохронность определяется рядом причин. Первая из них аналогична соответствующей причине неизохронности одноконтурных LC-автогенераторов. Она порождается нелинейными инерционными свойствами АЭ, а именно, зависимостью фазы крутизны тока АЭ от амплитуды колебаний. Поскольку фазовые соотношения в автогенераторе определяют частоту автоколебаний, изменение фазы крутизны ведет к изменению частоты автоколебаний как в переходном, так и в стационарном режимах.

Вторая причина неизохронности определяется существенной частотной зависимостью управляющего сопротивления в полосе частот возможных автоколебаний вблизи частоты ω_k. Частотная зависимость управляющего сопротивления R приводит к неизохронности только в переходном режиме и определяется параметром неизохронности H. Величина Н равна нулю, если R(ω) вблизи ω_k в первом приближении от частоты не зависит, т. е. dR/dω|_{ω = ωk} = 0, например, когда R(ω) принимает на частоте ω_k максимальное значение. Отличие Н от нуля будет на скатах частотной зависимости R(ω). По этой причине рассматриваемый автогенератор может быть неизохронным даже с безынерционным АЭ. В этом отношении рассматриваемый автогенератор во многом аналогичен автогенератору с контуром между коллектором и базой [80].

Третьей причиной неизохронности, как видно из (2.20), является изменение входного тока АЭ при изменении амплитуды колебаний. Причем здесь важную роль играет не только реактивная, но и активная составляющая первой гармоники входного тока. Это связано с тем, что изменение нелинейной составляющей входного тока АЭ эквивалентно изменению собственной проводимости Y₁₁ линейной системы автогенератора. Последнее приводит к изменению фазового сдвига на входе 1-1' линейной системы, а следовательно, и к изменению частоты автоколебаний при изменении амплитуды колебаний как в переходном, так и в стационарном режимах.

При сделанных предположениях укороченные уравнения (2.20) справедливы и для автогенераторов с широкополосной линией задержки. В этом случае Г (ω) и Ψ_о.сω) не зависят от частоты, т. е. величины Г'/Г и WVc при этом равны нулю.

Уравнения (2.20) получены для одночастотного режима. Для п частотного режима необходимо записать п укороченных уравнений (2.20) по числу рассматриваемых собственных частот линейной резонансной системы автогенератора. При этом токовые коэффициенты S_||, S_⊥, s_a, s_p будут зависеть не только от амплитуд всех типов колебаний, но и от их фазовых соотношений. Коэффициенты уравнений для разных типов колебаний (т. е. для разных собственных частот ω_k) будут в общем случае различны. Многочастотные режимы автогенераторов с устройствами на ПАВ будут рассмотрены в гл. 3.

Уравнения (2.20) не учитывают в явном виде зависимость режима автогенератора от наличия цепей автосмещения. Однако в неявном виде эта зависимость учитывается, если постоянная времени цепей смещения существенно меньше постоянной времени переходных процессов автогенератора. Действительно, если применяется наиболее общий тип автосмещения - комбинированный, то в предположении, что входной и выходной токи АЭ зависят лишь от входного напряжения, напряжение автосмещения при заданных сопротивлениях резисторов его цепи зависит также лишь от u₁. Следовательно, входной и выходной токи АЭ, зависящие и от напряжения автосмещения, в конечном счете зависят лишь от уровня входного напряжения. Таким образом, получаем некоторую эквивалентную зависимость токов i₁ и i₂ от u₁, в которую в качестве параметров будут входить сопротивления резисторов автосмещения, т. е. для рассматриваемого случая будут справедливы уравнения (2.20).

Иное дело, если постоянные времени цепей автосмещения соизмеримы с постоянной времени автогенератора. В этом случае уравнения (2.20) должны быть дополнены уравнениями, описывающими цепи автосмещения. Поскольку при этом возможно возникновение прерывистой генерации, то такой случай с точки зрения практики не очень интересен.

Полученные укороченные уравнения, а следовательно, и процессы, протекающие в автогенераторах, будут различаться для различных устройств на ПАВ при разных схемах их включения. Поэтому рассмотрим далее полученные результаты для конкретных схем автогенераторов.