3.6. Взаимодействие колебаний кратных частот

В автогенераторах на ПАВ возможно существование двухчастотных колебаний кратных частот. Наиболее интересным для практики является случай существования колебаний основной частоты и колебания на частоте приблизительно в 2 раза большей основной.

В предположении, что ток АЭ можно аппроксимировать в виде

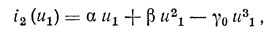
получим следующие нормированные укороченные уравнения рассматриваемого автогенератора:

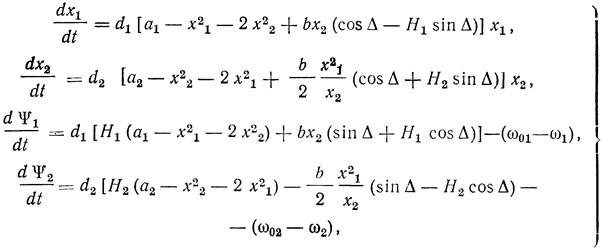
где

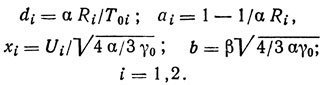
В аппроксимации тока (3.20) учитывается квадратичный член с коэффициентом β.

Необходимо отметить, что полученные укороченные уравнения (3.21) более сложны, чем соответствующие уравнения для двухчастотного двухконтурного автогенератора с отношением частот 1:2 [116, 117]. Это объясняется изменением параметров линейной резонансной системы автогенератора в полосе частот возможных колебаний. Все это усложняет зависимость стационарных амплитуд колебаний от параметров. Более сложным будет и характер переходных процессов.

Из (3.21) следует, что если собственные частоты линейной резонансной системы точно кратны, т. е. ω₂ = 2ω₁, то разность фаз двух колебаний Δ равна или нулю, или я подобно обычному двухчастотному LC-генератору с кратностью частот 1:2. Стационарные амплитудные уравнения при этом аналогичны стационарным амплитудным уравнениям двухчастотных LC-генераторов [116], следовательно, и их нагрузочные характеристики будут аналогичны.

Рассмотрим случай, когда амплитуда x₁ колебаний на основной частоте ω₁ существенно превышает амплитуду колебаний на другой частоте х₂. В этом случае первая из них приближенно такая же, как в одночастотном режиме, т. е.

Амплитуду колебаний на кратной частоте можно при этом приближенно определить как

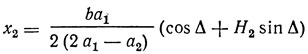
или

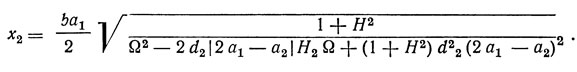
Амплитуда х₂ принимает максимальное значение

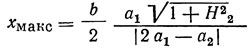
при частотной расстройке Ω₁ = d₂H₂|2a₁ - а₂|. При расстройке от значения Ω₁ амплитуда колебаний х₂ монотонно уменьшается. Как показывает анализ, подобный случай может быть, если

Используя стационарные уравнения (3.21) для автогенератора с несогласованной ЛЗ ПАВ, можно получить следующее выражение для относительной нестабильности частот колебаний δω₀₁ и δω₀₂ в режиме синхронизма при ω₂ = 2ω₁, если эти нестабильности определяются медленными изменениями собственных частот автогенератора δω₁ и δω₂:

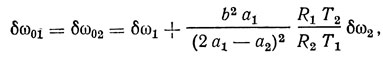
где Т₁, Т₂ - времена задержки в ЛЗ ПАВ на частотах ω₁ и ω₂.

Нестабильность частоты δω₁ полностью переносится на нестабильность частоты стационарных колебаний.

Если собственная частота ω₂ нестабильна, то эта нестабильность, как следует из (3.25), может переноситься на нестабильность стационарных частот автогенератора. Поскольку времена задержки Т₁, Т₂ для одной линии задержки можно считать приблизительно одинаковыми, то, увеличивая или уменьшая соотношения R₁/R₂, можно изменять коэффициенты влияния нестабильностей собственных частот колебаний.

Из (3.25) видно, что в таком режиме можно обеспечить стабильные колебания на удвоенной частоте, даже если параметры резонансной системы автогенератора на этой частоте не являются достаточно стабильными. Требуемая стабильность обеспечивается стабильными колебаниями на более низкой, основной частоте.

Рассмотрим теперь случай, обратный рассмотренному, т. е. будем считать, что в автогенераторе доминируют колебания на удвоенной частоте, т. е. x₂ >> x₁. В этом режиме амплитуда колебаний на частоте ω₀₂ приближенно равна

Амплитуда колебаний на частоте ω₀₁, как следует из (3.21), определяется из выражения

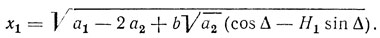
Будем предполагать, что |а₁ - 2а₂| << b √а₂(1+H²₁). Тогда разность фаз колебаний

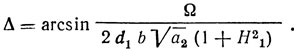
При этом полосу синхронизма можно оценить как

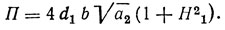
Зависимость амплитуды колебаний x₁ от расстройки Ω имеет вид

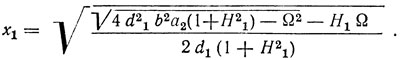
Из (3.26) следует, что x₁ принимает максимальное значение

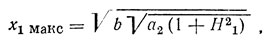
если расстройка

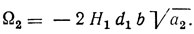
При расстройке частоты от значения Ω₂ амплитуда x₁ монотонно убывает до нуля на границе полосы синхронизма.

Для рассматриваемого режима деления частоты в автогенераторе на несогласованной ЛЗ ПАВ справедливо следующее выражение для нестабильностей частоты (если ω₂ = 2ω₁):

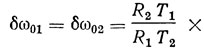
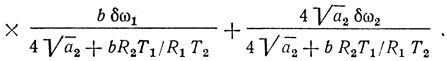
Нестабильность частоты колебаний определяется, в основном, нестабильностью частоты бог, если

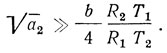
Поскольку (как указывалось выше) можно приближенно считать T₁ ≈ T₂, то неравенство (3.27) будет иметь вид 4R₁x₂ >> bR₂.