3.5. Асинхронные взаимодействия колебаний

Как уже указывалось в гл. 2, укороченные уравнения (2.20) можно использовать для исследования многочастотных колебаний в автогенераторах на ПАВ. Каждой из частотных составляющих многомодового процесса соответствуют укороченные уравнения вида (2.20). Для каждой из них коэффициенты уравнений (2.20) будут различаться. Токовые коэффициенты уравнений зависят от амплитуд всех частотных составляющих и от их фазовых соотношений. Для асинхронных взаимодействий токовые коэффициенты зависят лишь от амплитуд частотных составляющих автоколебательного процесса [113-117].

Рассмотрим асинхронное взаимодействие двух типов колебаний в автогенераторе с ЛЗ ПАВ. Из материала гл. 2 следует, что в полосе пропускания главного лепестка ЛЗ ПАВ может оказаться несколько собственных частот линейной резонансной системы автогенератора. Предположим, что параметры ЛЗ ЛАВ таковы, что этих частот две. Тогда, аппроксимируя зависимость выходного тока АЭ от напряжения двучленом i₂ = αu₁ - γ₀u³₁, получим следующие нормированные укороченные уравнения:

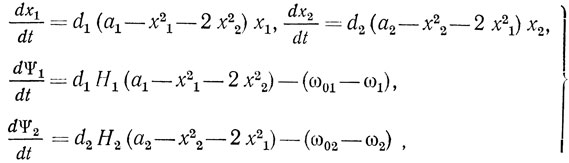
где d_i = αR_i/T_0i; ω₀₁ - стационарная частота колебаний первой моды, ω₀₂ - стационарная частота колебаний второй моды;

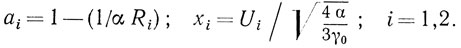
Индекс i в уравнениях (3.18) соответствует i-му типу колебаний, т. е. i-й моде колебаний.

Из (3.18) видно, что в стационарном режиме частоты колебаний равны собственным частотам линейной резонансной системы ω₁ и ω₂.

Особенностью рассматриваемого автогенератора является то, что, как следует из (3.18), мгновенные частоты двух типов колебаний в переходном режиме зависят от амплитуд колебаний. Причем частота, например, первого типа колебаний зависит не только от амплитуды первого типа колебаний, но и от амплитуды второго.

Поскольку амплитудные уравнения не зависят от фазовых, то исследование устойчивости стационарных колебаний сводится к исследованию устойчивости решений первых двух (амплитудных) уравнений (3.18). Эти уравнения аналогичны соответствующим уравнениям двухчастотного асинхронного LC-генератора [116], которые достаточно хорошо изучены. Известно, что режим одновременного существования двух типов колебаний для рассматриваемой характеристики нелинейности в таких генераторах невозможен. Следовательно, он невозможен и в рассматриваемом автогенераторе, т. е. возможен лишь одночастотный режим на частоте либо первого, либо второго типа колебаний в зависимости от начальных условий.

Сказанное справедливо, если не учитывается возможность возникновения типов колебаний, набег фазы для которых по кольцу обратной связи автогенератора равен нечетному числу π. О них упоминалось в § 2.4. Там же было сказано, что эти типы колебаний проявляют себя лишь при условии, что автогенератор работает на падающем участке колебательной характеристики. Этот участок для транзисторных генераторов соответствует сильно перенапряженному режиму, весьма редко используемому на практике. Однако этому режиму соответствует весьма интересная особенность - возможность существования многочастотных асинхронных режимов при мягкой колебательной характеристике автогенератора. Это легко проиллюстрировать для двухчастотной системы, в которой для одной из частот набег фазы по кольцу обратной связи равен нечетному числу π. Возможный фазовый портрет системы, соответствующий случаю устойчивого двухчастотного режима, изображен на рис. 3.9.

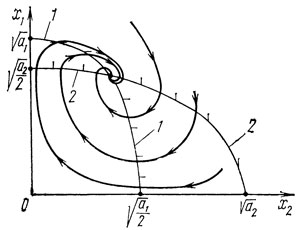
Рис. 3.9. Фазовый портрет двухчастотной системы: 1 - линия dx₁/dt = 0; 2 - линия dx₂/dt = 0

Одной из важнейших характеристик автогенератора является полоса перестройки по частоте. В автогенераторе на ЛЗ ПАВ она может быть осуществлена, например, изменением фазового сдвига в дополнительном звене, включенном последовательно с ЛЗ ПАВ. Если первоначально частота колебаний была равна частоте акустоэлектрического синхронизма ω_а, то три перестройке она отходит от нее, а частота соседнего тина колебаний при этом может приближаться к ω_а. При этом управляющее сопротивление для первого типа колебания уменьшается с расстройкой, а для второго - растет. Возможна ситуация, когда за счет изменения условий генерации для этих двух частот первый тип колебаний пропадает, а генерация возникает на втором типе колебаний, т. е. произойдет скачок режима и частоты, что обычно нежелательно.

Рассмотрим, насколько можно перестраивать систему, не боясь возбуждения другого типа колебаний. Используя результаты [116], можно показать, что скачков режима и частоты не будет в пределах полосы

для симметричной ЛЗ ПАВ и

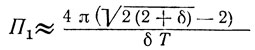
для несимметричной ЛЗ ПАВ, где П₁ - максимальная полоса перестройки, внутри которой существует одночастотный режим без скачков частоты.

Из (3.19 а, б) следует, что при увеличении запаса по самовозбуждению δ возможный диапазон перестройки уменьшается. Это объясняется улучшением условий возбуждения паразитного типа колебаний.