§ 9. Влияние высших гармоник на режим работы ламп и к.п.д. УРУ

Остановимся теперь на вопросе о влиянии высших гармоник на работу УРУ на фильтрах нижних частот типа m. При этом рассмотрим отдельно работу усилителя во второй половине диапазона частот (f₁ > 0,5f_га) и в первой его половине (f₁ < 0,5f_гa).

Вторая половина диапазона частот (f₁ > 0,5f_гa). Если частота напряжения возбуждения f₁ (первой гармоники токов ламп) лежит в рассматриваемом участке диапазона, то все высшие гармонические лежат вне полосы прозрачности анодной линии. Следовательно, в этом случае анодная линия будет отфильтровывать высшие гармоники.

Действительно, постоянная распространения анодной линии для частот высших гармоник (r ≥ 2)

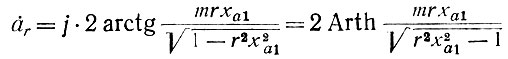
будет вещественным числом, поскольку rх_а1 > 1 и наличие экспоненциальных множителей вида

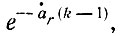
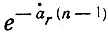
в выражениях (40) и (42) будет приводить к тому, что высшие гармоники в напряжениях на анодах ламп окажутся весьма малыми. Как показывают расчеты по формулам (40) и (42) при f₁ ≥ 0,55f_гa, отношение амплитуды второй гармоники к амплитуде первой гармоники на анодах ламп и выходе УРУ при n > 4 удовлетворяет следующему неравенству [32]:

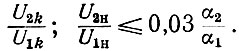
Уровень третьей и других гармоник оказывается еще меньше. Поэтому при анализе режимов работы ламп всеми высшими гармоническими можно пренебречь и подобно тому, как это делается для резонансных усилителей, считать колебательное напряжение на анодах ламп и выходе УРУ синусоидальным. Величина этих напряжений будет определяться формулами, аналогичными (15) и (25).

Первая половина диапазона частот (0 < f₁ ≤ 0,5f_га). На этом участке диапазона частота некоторых из высших гармоник лежит в полосе прозрачности анодной линии, а частота остальных гармоник - вне этой полосы. Напряжениями гармоник, лежащих вне полосы прозрачности, как и в предыдущем пункте, можно пренебречь. При этом номер наивысшей гармоники, лежащей в полосе УРУ, будет равняться отношению f_гa/f₁, округленному до ближайшего меньшего целого числа. Следовательно, в выражениях (43)-(45) за верхний индекс суммирования может быть принято округленное отношение f_гa/f₁.

Будем сперва предполагать, что частоты основных гармоник лежат на участке диапазона, соответствующем 0 ≤ х_ar ≤ 0,85. В этом случае фазовая характеристика звеньев анодной линии для m = 1,4 оказывается весьма линейной (рис. 9, б), так что можно считать, что

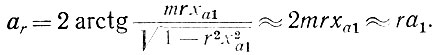
Кроме того, в этом случае можно пренебречь частотной зависимостью множителей А̇_r и В̇_r в (40)-(42) и считать, что для всех гармоник они одинаковы (А̇_r = А̇₁; В̇_r = В̇₁). С учетом этих допущений выражение (40) для выходного напряжения в первой половине диапазона частот можно подстановкой в него (46) привести к виду:

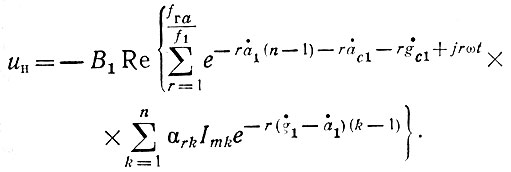
Подставляя в последнюю формулу В₁ ≈ 0,5ρ_а, получим для случая ġ₁ = а̇₁ при одинаковых углах отсечки θ_k, и одинаковых максимальных значениях тока ламп I_mk следующее выражение для выходного напряжения:

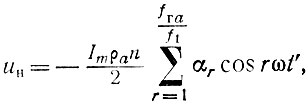
где

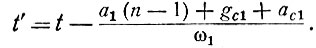
Из сравнения последнего выражения с (32) и (36) видно, что форма выходного напряжения при f_га/f₁ >> 1 практически повторяет форму переменной составляющей импульсов анодного тока ламп с обратным знаком. Однако импульсы выходного напряжения смещены во времени относительно импульсов тока ламп.

Переменное напряжение на аноде последней лампы u_n будет иметь такую же форму, как и выходное напряжение, так что результирующее напряжение на аноде последней лампы u_аn с учетом постоянного напряжения питания Е_а определится следующим образом:

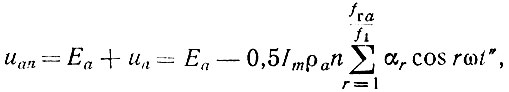
где

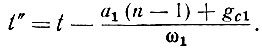
На рис. 18, б представлен график зависимости u_аn от ωt' для угла отсечки анодного тока θ = 90°. На этом же рисунке штриховой линией представлен график того же напряжения при учете только первой и второй гармоник, т. е. для f_га/f₁ = 2. Как видно из рис. 18, б, гармоники выше второй мало влияют на форму выходного напряжения. Поэтому при углах отсечки порядка 90° можно считать, что выходное напряжение и напряжение на аноде последней лампы повторяют форму импульсов анодного тока практически во всей первой половине диапазона частот.

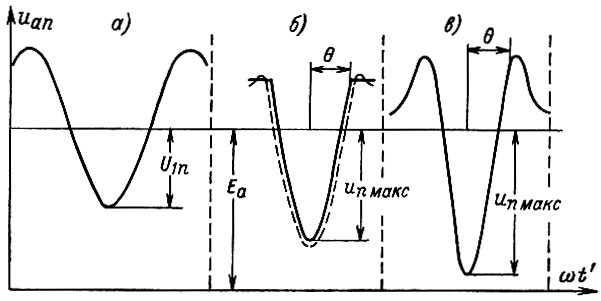
Рис. 18. Форма напряжения на аноде последней лампы УРУ в режиме колебаний второго рода: а - во второй половине диапазона частот; б - в первой половине диапазона для однотактной схемы; в - в первой половине диапазона (х_а1 = 0,35) для двухтактной схемы

Что касается напряжений на анодах остальных ламп, то они будут иметь достаточно сложную форму, определяемую относительными фазами и амплитудами гармоник в соответствии с выражениями (42) и (45). Не исследуя детально напряжение на анодах этих ламп, ограничимся следующим важным выводом, который можно сделать на основе выражения (42): уровень высших гармоник на анодах ламп не превышает уровня высших гармоник на аноде последней лампы. Справедливость этого утверждения вытекает из того, что обратные волны токов высших гармоник [второе слагаемое в квадратных скобках (42)], так же как и первых гармоник (см. § 7), складываются несинфазно. Сделанный вывод будет использован при расчете к. п. д. усилителя.

Предположение о постоянстве коэффициентов В̇_r и А̇_r для всех гармоник и о линейности фазовой характеристики звеньев анодной линии справедливо только для диапазона, соответствующего 0 < x_ar ≤ 0,85. Если частота одной из гармоник f_r лежит в пределах 0,85f_гa < f_r < f_га, указанные допущения оказываются несправедливыми.

При f_r → f_гa множители В̇_r и А̇_r резко возрастают, поскольку Z_пar → ∞, и возникает возможность "подчеркивания" гармоники, что является нежелательным для работы УРУ.

Наибольший интерес представляет случай, когда частота второй гармоники лежит в районе граничной частоты анодной линии (f₂ → f_га), поскольку из всех высших гармонических вторая обычно оказывается наиболее сильной и при "подчеркивании" она может оказаться соизмеримой с основной гармоникой или даже превосходить ее. Выражение для модуля амплитуды второй гармоники на выходе УРУ при θ_k = const и I_mk = const можно записать на основе (40) в виде:

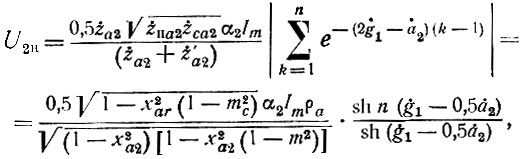
где

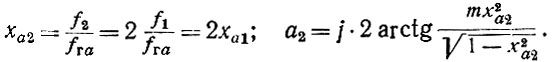
Подкоренное выражение знаменателя при х₂ → 1 уменьшается, что приводит к увеличению U_2н. Однако второй сомножитель (48) с возрастанием х_а2 также уменьшается, поскольку за счет нелинейности фазовой характеристики (которой нельзя пренебрегать при х₂ → 1) ġ₁ ≠ 0,5ȧ₂, даже если ġ₁ = а̇₁. Следовательно, в схеме УРУ вторые гармоники токов ламп складываются несинфазно при синфазном сложении первых гармоник тока. Таким образом, в режиме колебаний второго рода в УРУ автоматически реализуется способ коррекции частотной характеристики для второй гармоники, подобный описанному в § 5.

Из выражения (48) видно, что несинфазность вторых гармоник токов будет проявляться тем сильнее, чем больше n, поскольку второй сомножитель (48) тем меньше при заданной разности (ġ₁ - 0,5ȧ₂), чем больше n. Как показывают расчеты [32], при n ≥ 10 возрастание первого сомножителя выражения (48) при x_a2 → 1 компенсируется уменьшением второго сомножителя, так что амплитуда второй гармоники при 0,85 ≤ х_a2 ≤ 1 оказывается даже меньше, чем для х_a2 << 0,85.

При п = 3÷6 первый сомножитель возрастает быстрее, чем уменьшается второй, в результате чего вторая гармоника напряжения для указанного числа ламп возрастает при x_a2 → 1, что является нежелательным.

Для уменьшения второй гармоники в этом случае целесообразно делать неравными граничные частоты анодной и сеточной линии, подобно тому, как это описано в § 5. Однако если коррекция частотной характеристики по первой гармонике возможна как в случае

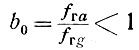
так и b₀ > 1, то для уменьшения уровня второй гармоники обязательно, чтобы

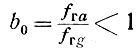
Последнее обусловлено тем, что для второй гармоники уже имеет место несинфазность сложения их токов (причем g₁ < 0,5а₂) и задача заключается лишь в увеличении степени этой несинфазности, что требует g₁ < а₁.

Величину b₀ можно выбирать такой же, как и для коррекции частотной характеристики УРУ по первой гармонике (при b₀ < 1). При этом, если первая гармоника напряжения будет почти постоянна во всем диапазоне частот (рис. 12, а), то вторая будет уменьшаться при х_a2 → 1, поскольку несинфазность сложения вторых гармоник токов будет проявляться сильнее, чем для первых, в силу нелинейности фазовой характеристики анодной линии.

Таким образом, широкополосные свойства анодной линии УРУ приводят к тому, что в первой половине диапазона частот напряжение на выходе усилителя и на анодах ламп содержит неослабленные высшие гармонические. Мощность первой гармоники при критическом или недонапряженном режиме УРУ оказывается, как и в классе А, весьма постоянной в диапазоне частот, так что усилитель сохраняет свои широкополосные свойства.

Величина мощности первой гармоники на выходе УРУ при одинаковых углах отсечки токов ламп составляет

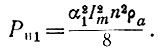
Найдем к. п. д. усилителя по первой гармонике, учитывая влияние высших гармонических. Постоянное анодное напряжение УРУ для обеспечения критического режима

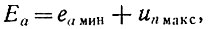
где u_{n макс} = u_н.макс - максимальное мгновенное значение отрицательной полуволны переменного напряжения на аноде последней лампы (на нагрузке) - рис. 18.

Для второй половины диапазона частот выходное напряжение гармоническое (рис. 18, а) и

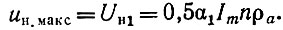
Для первой половины диапазона u_н.макс можно найти, используя выражение (47) для t' = 0:

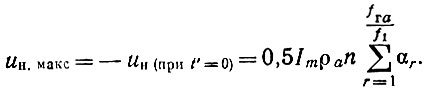
Учитывая, что для коэффициентов разложения косинусоидального импульса выполняется равенство [4]:

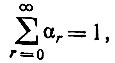
получим

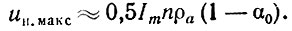
Поскольку (1 - α₀) > α₁, максимальное мгновенное значение выходного напряжения для первой половины диапазона частот за счет влияния высших гармоник больше, чем для второй половины диапазона. Следовательно, постоянное анодное напряжение для обеспечения критического режима УРУ

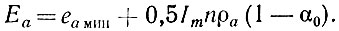
При полученном анодном напряжении последняя лампа будет работать при f₁ < 0,5f_гa в критическом режиме, однако при f₁ > 0,5f_га режим этой лампы будет недонапряженным.

К. п. д. усилителя в режиме колебаний второго рода найдем, используя выражения (49) и (50):

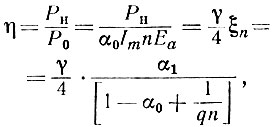
где q = 0,5S_кpρ_а; S_кр = I_m/e_aмин; ξ_n = U_1n/E_a - коэффициент использования анодного напряжения последней лампы УРУ по первой гармонике.

Коэффициенты разложения α₁ и α₀ зависят от угла отсечки θ в соответствии с выражениями (37) и (38). Используя эти выражения, можно проанализировать зависимость η от угла отсечки. На рис. 19 построены графики зависимости η от θ, из которых видно, что при θ = 90÷110° к. п. д. достигает максимального значения, которое больше, чем к. п. д. в режиме колебаний первого рода (θ = 180°). Однако максимальное значение к. п. д. не превышает 0,3 и эффективность повышения к. п. д. оказывается весьма малой. Так, при qn → ∞ к. п. д. за счет работы с отсечкой анодного тока может быть увеличен по сравнению с режимом класса А всего лишь в 1,2 раза, в то время как для резонансного усилителя выигрыш в к. п. д. может быть достигнут значительно больше (в 1,5-1,7 раза).

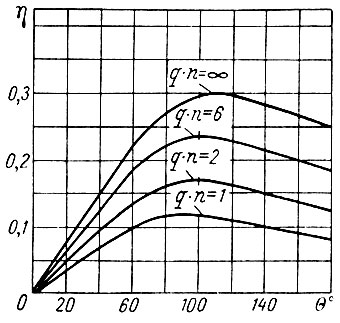
Рис. 19. Зависимость к. п. д. однотактного УРУ от угла отсечки анодного тока при различных значениях параметра qn

Малая эффективность повышения к. п. д. обусловлена тем, что одновременно с ростом у в режиме колебаний второго рода из-за влияния высших гармоник уменьшается коэффициент использования анодного напряжения по первой гармонике n-й лампы, так что этот коэффициент оказывается меньше, чем в классе А, при том же уровне первой гармоники.

Низкое значение предельного к. п. д. (η ≤ 0,3) объясняется, как и в режиме колебаний первого рода, плохим использованием анодного напряжения первых ламп УРУ по сравнению с последней, для которой ξ_n может быть достаточно высоким.

Наличие неослабленных высших гармонических в первой половине диапазона частот ограничивает возможность применения режима колебаний второго рода для однотактного УРУ.

Применяя двухтактную схему УРУ, можно значительно уменьшить уровень гармоник в выходном напряжении и в то же время существенно увеличить к. п. д. усилителя. Однако работа двухтактной схемы УРУ имеет существенные особенности по сравнению с двухтактными усилителями других типов, поэтому целесообразно посвятить двухтактной схеме УРУ специальный раздел.