§ 8. Особенности работы УРУ в режиме колебаний второго рода

Как известно, одним из эффективных способов повышения к. п. д. электронных усилителей является использование нелинейных свойств ламп. Так, при несинусоидальной форме тока ламп (в режиме колебаний второго рода) энергетические соотношения в резонансных усилителях значительно улучшаются [4]. Поэтому целесообразно исследовать работу УРУ в этом режиме и выяснить возможность повышения его к. п. д.

Следует ожидать, что работа УРУ в режиме колебаний второго рода будет существенно отличаться от работы резонансных усилителей. Это отличие обусловлено тем, что в силу широкополосных свойств УРУ напряжения на выходной линии будут содержать на некоторых участках диапазона достаточно интенсивные высшие гармонические, в то время как в резонансных усилителях можно считать, что все высшие гармонические отфильтровываются и напряжение на аноде лампы синусоидально при несинусоидальном токе.

Наличие высших гармонических в напряжениях на выходной линии может существенно влиять на режим работы ламп, на выбор постоянных напряжений питания, а следовательно, и на энергетические показатели УРУ.

При анализе работы УРУ в режиме колебаний второго рода будем пользоваться кусочно-линейной аппроксимацией ламповых характеристик (рис. 13), а входное напряжение будем считать гармоническим с частотой f₁ = ω₁/2π. В этом случае ток ламп УРУ в недонапряженном режиме будет иметь форму косинусоидальных импульсов с углом отсечки 9 (рис. 13, в), величина которого определяется параметрами лампы, амплитудой входного напряжения и напряжением смещения E_g1 (рис. 13, б).

Ток каждой лампы может быть представлен в виде ряда Фурье:

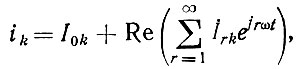
где

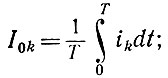
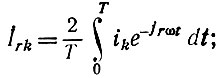
k - номер лампы УРУ; r - номер гармоники тока; I_rk - комплексная амплитуда r-й гармоники тока k-й лампы; I_0k - постоянная составляющая тока k-й лампы; Т = 1/f₁ = 2π/ω₁ - период входного напряжения.

Импульсы тока различных ламп будут сдвинуты во времени в соответствии с фазовым сдвигом напряжений на сетках этих ламп. С учетом этого сдвига, определяемого формулой (14), выражение для тока k-й лампы в полосе прозрачности сеточной линии (f₁ > f_rg) можно записать в виде:

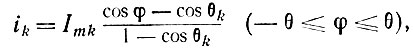
где φ = ωt - g_c1 - g₁; I_mk - максимальное значение тока k-й лампы (рис. 13, в); θ_k - угол отсечки тока k-й лампы; g_c1, g₁ - модули постоянных распространения звеньев входной линии для первой гармоники - см. формулы (11) и (13).

Используя (35), нетрудно получить выражения для комплексных амплитуд гармоник токов ламп, вычислив интеграл (33):

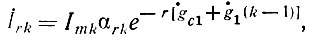
где

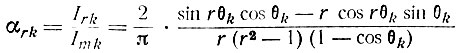
есть коэффициент i-й гармоники тока k-й лампы (коэффициент Берга).

Постоянная составляющая токов ламп определится выражением:

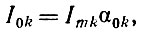
где

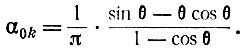
Как было показано в § 3, эквивалентная схема УРУ по выходной цепи в режиме колебаний второго рода может быть представлена в виде, изображенном на рис. 17, где в каждой секции анодной линии включены параллельно генераторы тока всех гармоник. Комплексные амплитуды этих генераторов определяются выражением (36).

Рис. 17. Эквивалентная схема анодной цепи УРУ в режиме колебаний второго рода

К эквивалентной схеме рис. 17 применим принцип суперпозиции. Используя этот принцип, получим общие соотношения для УРУ в режиме колебаний второго рода при характеристическом согласовании линий.

Комплексная амплитуда напряжения r-й гармоники на выходе усилителя определится в виде суммы:

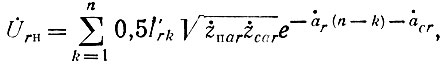
где r - номер гармоники.

Индекс r при характеристических сопротивлениях и постоянных распространения указывает, что следует брать значения этих величин для частоты r-й гармоники.

Учитывая, что

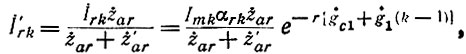
получим

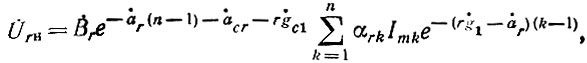
где

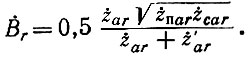
Аналогично можно найти комплексную амплитуду r-й гармоники на балластном сопротивлении, суммируя напряжения обратных волн от всех ламп:

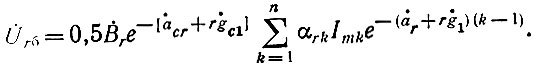
Напряжение r-й гармоники на аноде k-й лампы можно найти, просуммировав напряжения прямых волн от первых k ламп и обратных волн от последующих (n - k) ламп:

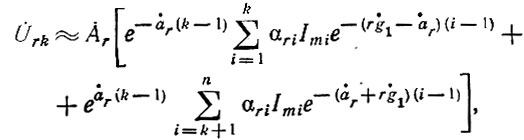
где

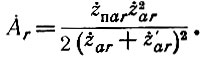
При выводе последнего выражения не было учтено малое падение напряжения на сопротивлении ż'_а (рис. 7, а). Максимальные значения токов ламп при принятой аппроксимации характеристик (рис. 13, б и в) определяются из выражения:

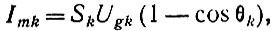
где S_k - крутизна анодно-сеточной характеристики k-й лампы.

Мгновенные значения напряжений на нагрузке R_н, на балластном сопротивлении R_б и на аноде k-й лампы находятся по известным комплексным амплитудам гармоник следующим образом:

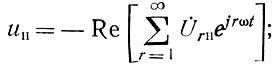
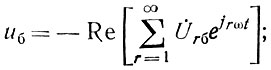
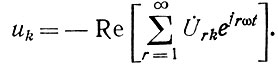
Знак минус перед последними выражениями учитывает, что все напряжения отсчитываются относительно общей точки - земли.

Полученные общие соотношения позволяют проанализировать работу УРУ в режиме колебаний второго рода при характеристическом согласовании для каждой конкретной структуры анодной линии. Однако, не проводя пока подробного анализа, сделаем на основе полученных выражений ряд важных общих выводов о работе УРУ в нелинейном режиме.

Прежде всего нетрудно заметить, что при подстановке в формулы (40)-(42) r = 1, получим выражения, аналогичные выражениям § 5, 6, 7. Разница будет заключаться в том, что в этих формулах будут фигурировать относительные частоты первой гармоники х₁ = f₁/f_rg, x_g1 = f₁/f_rg и амплитуды первой гармоники токов, причем

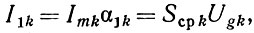
где S_{cp k} = a_1k (1 - cosθ_k)⋅S_k - средняя крутизна k-й лампы по первой гармонике.

Следовательно, все диапазонные свойства токов и напряжений УРУ, отмеченные в предыдущих параграфах для линейного режима, остаются справедливыми для первых гармоник токов и напряжений в режиме колебаний второго рода. В частности, отдельные лампы УРУ будут весьма неравномерно использоваться в середине диапазона по напряжению и мощности первой гармоники, что должно проявляться в низком значении к. п. д. УРУ по сравнению с резонансными усилителями.

Уровень высших гармоник в напряжениях УРУ будет определяться соотношением частоты гармоник f_r = rf₁ и граничной частоты анодной линии f_га, поскольку характеристические сопротивления и постоянные распространения в полосе прозрачности анодной линии (0 ≤ f_r < f_гa) и за пределами этой полосы ведут себя различно.

Полученные выражения позволяют отметить еще одну важную особенность УРУ в режиме колебаний второго рода. Так, из формулы (36) видно, что амплитуды и фазы токов всех гармонических составляющих определяются модулем и фазой коэффициента передачи соответствующего участка сеточной линии для частоты первой гармоники f₁ (для частоты напряжения возбуждения) и не зависят от модуля и фазы коэффициента передачи для частоты самой гармоники f_r = rf₁. При прохождении же анодной линии амплитуды и фазы токов изменяются в соответствии с модулем и фазой коэффициентов передачи участков анодной линии именно для частоты самих рассматриваемых гармоник. Это приводит к тому, что прямые волны токов высших гармонических (r ≥ 2) могут складываться несинфазно даже в том случае, когда граничные частоты анодной и сеточной линий одинаковы (f_гa = f_гg; ġ₁ = а̇₁). Последнее будет иметь место тогда, когда зависимость постоянной распространения от частоты нелинейна и выполняется неравенство:

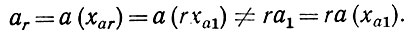
На отмеченную несинфазность указывает, в частности, выражение (40), где показатель экспоненциональных множителей е^{-(rġ₁-ȧ_r)(k-1)} не обращается в нуль для высших гармоник даже в том случае, если для первой гармоники показатель обращается в нуль (ġ₁ = а̇₁).