§ 13. Определение напряжений прямой и обратной волн в выходной линии УРУ

Использование системы характеристических параметров позволяет по аналогии с теорией длинных линий напряжение на выходных концах эквивалентной схемы (U̇_н и U̇_б) и на зажимах генераторов тока (U̇_i)^- представить в виде суммы двух составляющих, которые можно трактовать как прямую U⁺_i и обратную U^-_i волны:

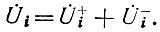
Рассмотрим более подробно процессы на i-м стыке двух четырехполюсников - i-го и (i + 1)-го (рис. 29).

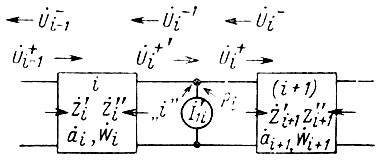
Рис. 29. Схема стыка i-гo и (i + 1)-го четырехполюсников неоднородной выходной линии УРУ

В силу того, что в месте стыка четырехполюсники не согласованы, напряжения прямой и обратной волн слева от генератора тока U̇⁺_i' и U̇^-_i' (на выходе i-го четырехполюсника) и справа от генератора тока U̇⁺_i и U̇^-_i (на входе (i + 1)-го четырехполюсника) различны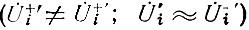

Однако для этих напряжений очевидно следующее равенство:

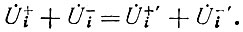
Второй закон Кирхгофа для узла i (рис. 29) может быть записан в виде [2]:

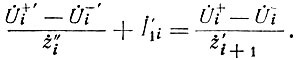
Систему уравнений (77) и (78) нетрудно записать в следующем виде:

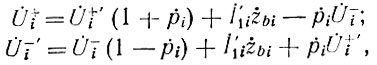
где 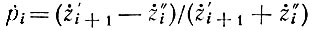- характеристический коэффициент отражения на i-м стыке четырехполюсников;

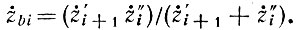
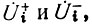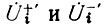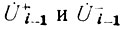В дальнейшем будем рассматривать только систему волн для чего в последних уравнениях выразим через на основе очевидных соотношений:

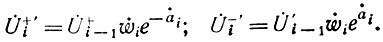
После указанных преобразований получим:

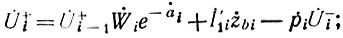
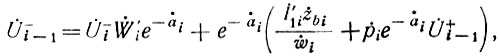
где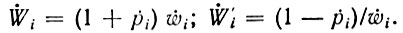

Аналогичные уравнения можно написать и для остальных n стыков четырехполюсников неоднородной линии.

Дальнейшие преобразования уравнений (79) и (80) целесообразно провести следующим образом.

Подставим в (79) вместо 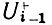его значение, которое можно представить в виде, аналогичном (79), при рассмотрении процессов на (i - 1)-м стыке четырехполюсников. Полученное выражение будет связывать U̇⁺_i и U̇⁺_i-2. Если далее вместо U̇⁺_i-2 подставить в это выражение формулу, аналогичную (79), которую можно получить из рассмотрения процессов на (i - 2)-ом стыке четырехполюсников, то можно установить связь между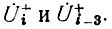

Проводя последовательно такие подстановки, выражение (79) можно привести к следующему виду:

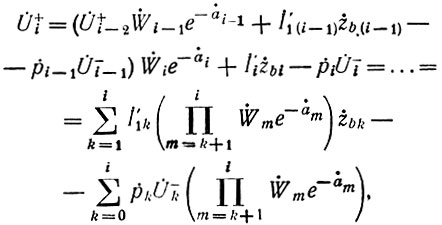
где i = 0, 1, 2, ..., n.

Здесь произведение 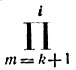принимается равным единице, если верхний индекс меньше нижнего.

Нулевое значение индекса k соответствует левому концу линии, так что 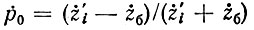равно коэффициенту отражения обратной волны от нагрузки ż_б с обратным знаком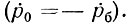

Если условиться, что сумма в выражении (81) равна нулю при верхнем индексе, меньшем нижнего, то это выражение справедливо и для "левого" нагрузочного конца (i = 0). Действительно, подстановка в (81) i = 0 дает очевидное уравнение:

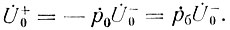
Дополученное выражение (81) показывает, что напряжение прямой волны на зажимах i-гo генератора тока является результатом воздействия первых i генераторов тока (первое слагаемое) и отражений обратной волны на стыках четырехполюсников, лежащих "слева" от i-го генератора, включая i-й стык (второе слагаемое).

Аналогичные преобразования можно провести с уравнением (80), выражая последовательно 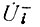через 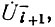затем 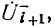через 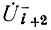и т. д., в результате чего получим

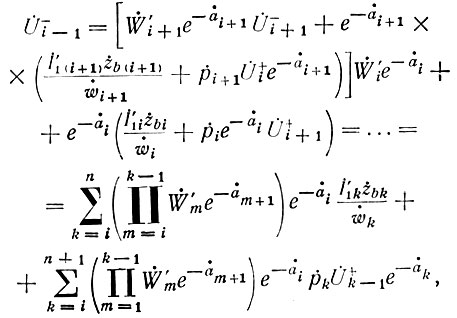
где i = 1, 2, 3,..., (n + 1).

Значение k = n + 1 соответствует "правому" нагрузочному концу линии, так что 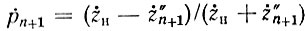равен коэффициенту отражения от нагрузки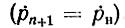

Из полученного выражения (82) видно, что обратная волна на зажимах (i - 1)-го генератора является результатом воздействия (n - i + 1) генераторов, включенных справа от (i - 1)-го генератора [первое слагаемое (82)], и отражений прямой волны от нагрузки и на стыках четырехполюсников в месте включения этих (n - i + 1) генераторов [второе слагаемое (82)].

Если написать уравнения (81) и (82) для всех указанных значений i, то получим систему 2 (n + 1) уравнений относительно 2 (n + 1) неизвестных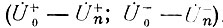

Эта система уравнений позволяет определить напряжения прямой и обратной волн, а следовательно, по формуле (76) и суммарное напряжение на зажимах любого из генераторов тока и на нагрузках усилителя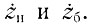

В принципе возможно точное решение этой системы, например, с использованием формул Крамера [12]. Однако вычисление определителей и миноров в этом случае является чрезвычайно трудоемким делом. Поэтому естественно воспользоваться одним из приближенных методов решения систем уравнений, наиболее простым из которых является итерационный метод (метод последовательных приближений [12]).

Выберем в качестве нулевого приближения для обратной волны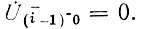

Тогда первое приближение для прямой волны в соответствии с (81) получим в виде:

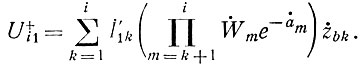
Используя теперь (83), получим с помощью (82) первое приближение для обратной волны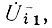

подставляя которое в (81), получим второе приближение для прямой волны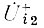

и т. д. В результате такого процесса последовательных приближений решение для прямой волны можно записать в виде ряда:

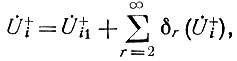
где

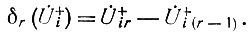
Если полученный ряд сходится, он дает точное решение системы. По этому решению можно отыскать с помощью (82) точное решение для обратной волны.

Получим достаточное условие сходимости ряда (84). Для этого (81) подставим в (85), используя при этом соответствующие приближения для обратной волны:

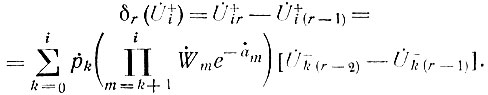
Если теперь выразить 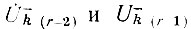через соответствующие приближения для прямой волны по формуле (81), то получим

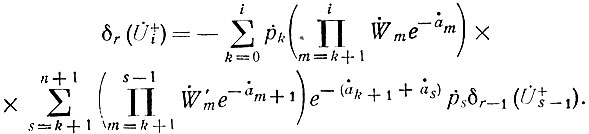
Последнее выражение позволяет написать следующее неравенство:

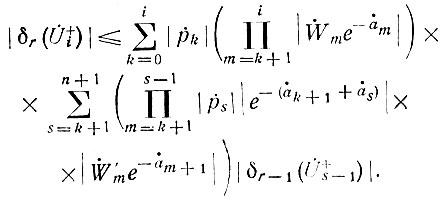
Если теперь учесть, что 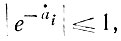то можно получить более грубую оценку:

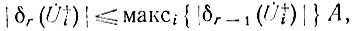
где

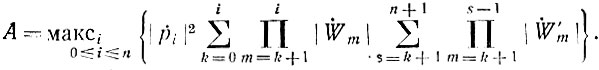
В последних выражениях символ макс_i означает максимальное значение величины, стоящей в фигурных скобках, при указанных значениях i.

На основе неравенства (86) можно сделать вывод, что ряд (84) мажорируется рядом

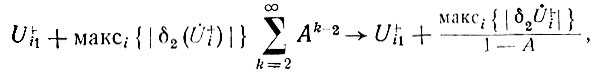
который сходится при А < 1. Отсюда получаем и достаточное условие сходимости ряда (84):

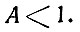
Оценим абсолютную погрешность k-го приближения для напряжения прямой волны:

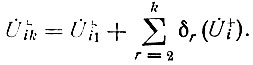
Учитывая формулу (84) и неравенство (86), можно получить искомую оценку:

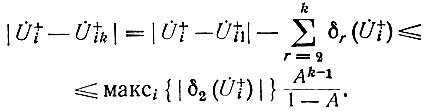
Для первого приближения имеем:

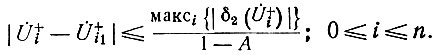
Как показывают расчеты, для тех значений коэффициентов отражения р_i, с которыми приходится иметь дело на практике, точность первого приближения оказывается достаточно высокой (единицы процентов). При этом в силу несинфазного сложения отраженных волн погрешность в значительной средней части диапазона частот существенно меньше, чем на концах диапазона (частотная зависимость погрешности обусловлена частотной зависимостью δ2(U̇_i⁺) в формуле (89). Полученные общие выражения позволяют при выполнении (87) рассчитать напряжения на зажимах любого генератора тока с любой наперед заданной точностью. Такие расчеты особенно важны для мощных усилителей, для которых необходимо знать режим работы каждой лампы и его зависимость от частоты.

Что касается частотной характеристики усилителя, то ее расчет может быть произведен с помощью полученных выражений при любом законе изменения волнового сопротивления. Если выполняется условие (87), то в зависимости от заданной точности по приведенной методике определяется соответствующее приближение для прямой волны на зажимах генератора тока 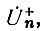а затем определяется выходное напряжение УРУ по формуле:

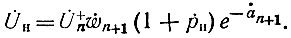
При этом свойства частотной характеристики определяются не только частотной зависимостью характеристических параметров, но и сложными интерференционными процессами в неоднородной линии.