
§ 11. Закон Ома
Соберем электрическую цепь (рис. 22, а), состоящую из аккумулятора 1 напряжением 2 в, рычажного реостата 2, двух измерительных приборов - вольтметра 3 и амперметра 4 и соединительных проводов 5. Установим в цепи при помощи реостата сопротивление, равное 2 ом. Тогда вольтметр, включенный на зажимы аккумулятора, покажет напряжение 2 в, а амперметр, включенный последовательно в цепь, покажет ток, равный 1 а. Увеличим напряжение до 4 в путем включения другого аккумулятора (рис. 22, б). При том же сопротивлении в цепи - 2 ом - амперметр покажет уже ток 2 а. Аккумулятор напряжением 6 в изменит показание амперметра до 3 а (рис. 22, в). Сведем наши наблюдения в табл. 4.
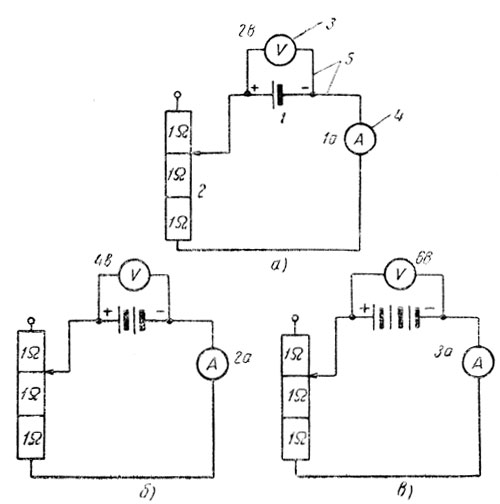
Рис. 22. Изменение тока в электрической цепи путем изменения напряжения цепи при неизменном сопротивлении

Таблица 4. Зависимость тока в цепи от напряжения при неизменном сопротивлении
Отсюда можно сделать вывод, что ток в цепи при постоянном сопротивлении тем больше, чем больше напряжение этой цепи, причем ток будет увеличиваться во столько раз, во сколько раз увеличивается напряжение.
Теперь в такой же цепи поставим аккумулятор с напряжением 6 в и установим при помощи реостата сопротивление в цепи, равное 1 ом (рис. 23, а). Тогда амперметр покажет 6 а. Увеличим реостатом сопротивление до 2 ом (рис. 23, б). Показание амперметра (при том же напряжении цепи) будет уже 3 а.
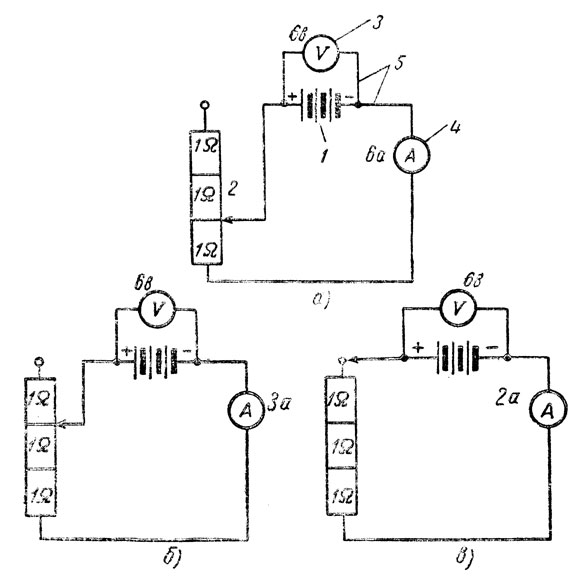
Рис. 23. Изменение тока в электрической цепи путем изменения сопротивления при неизменном напряжении
При сопротивлении в цепи 3 ом (рис. 23, в) показание амперметра будет 2 а.
Результаты опыта сведем в табл. 5.

Таблица 5. Зависимость тока в цепи от сопротивления при неизменном напряжении
Отсюда следует вывод, что при постоянном напряжении ток в цепи будет тем больше, чем меньше сопротивление этой цепи, причем ток в цепи увеличивается во столько раз, во сколько раз уменьшается сопротивление цепи.
Как показывают опыты, ток на участке цепи прямо пропорционален напряжению на этом участке и обратно пропорционален сопротивлению того же участка. Эта зависимость известна под названием закона Ома.
Если обозначим: I - ток в амперах, U - напряжение в вольтах, r - сопротивление в омах, то закон Ома можно представить формулой
I = U/r,
т. е. ток на данном участке цепи равен напряжению на этом участке, деленному на сопротивление того же участка.
Пример 10. Определить ток, который будет проходить по нити лампы накаливания, если нить имеет неизменное сопротивление 240 ом, а лампа включена в сеть с напряжением 120 в:
I = U/r = 120/240 = 0,5 a.
Пользуясь формулой закона Ома, можно определить также напряжение и сопротивление цепи:
U = I⋅r,
т. е. напряжение цепи равно произведению тока на сопротивление этой цепи, и
r = U/I,
т. е. сопротивление цепи равно напряжению, деленному на ток.
Произведение тока I, протекающего через какое-либо сопротивление, на величину этого сопротивления r называется падением напряжения на этом сопротивлении и обозначается буквой U:
U = I⋅r.
Пример 11. Какое нужно напряжение, чтобы в цепи с сопротивлением 6 ом протекал ток 20 а?
U = 1⋅r = 20⋅6 = 120 в.
Пример 12. По спирали электрической плитки протекает ток в 5 а. Плитка включена в сеть с напряжением 220 в. Определить сопротивление спирали электрической плитки:
r = U/I = 220/5 = 44 ом.
Если в формуле U = I⋅r ток равен 1 а, а сопротивление 1 ом, то напряжение будет равно 1 в:
1 а ⋅ 1 ом = 1 в.
Отсюда заключаем: напряжение в 1 в действует в цепи с сопротивлением 1 ом при токе в 1 а.
На рис. 24 приведена электрическая цепь, состоящая из источника электрической энергии, потребителя, имеющего сопротивление r, и длинных соединительных проводов, которые имеют сопротивление гл (сопротивление линии). При работе схемы, т. е. при прохождении по цепи электрического тока, показание вольтметра, включенного в начале линии U1, будет больше показания вольтметра, включенного в конце линии U2.
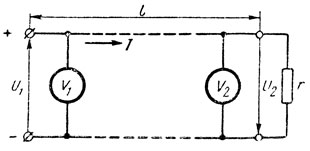
Рис. 24. Потеря напряжения в проводах
Такое уменьшение напряжения вдоль цепи по мере удаления от источника вызвано потерей напряжения в проводах ΔU:
ΔU = U1 - U2.
Потеря напряжения в линии происходит потому, что часть напряжения будет теряться в проводах линии. При этом потеря напряжения будет тем больше, чем больше ток линии и чем больше сопротивление проводов. Потеря напряжения равна току, протекающему по проводам линии, умноженному на сопротивление проводов:
U1 - U2 = ΔU = 2Iρ⋅l/S,
где U1 - напряжение в начале линии, в;
U2 - напряжение в конце линии, в;
I1 - ток линии, а;
ρ - удельное сопротивление проводов линии;
l - длина линии (в один конец), м;
S - сечение проводов, мм2.
Пример 13. От генератора, напряжение на зажимах которого 115 в, электроэнергия передается электродвигателю по проводам, сопротивление которых 0,1 ом. Определить напряжение на зажимах двигателя, если он потребляет ток в 50 а.
Очевидно, что на зажимах двигателя напряжение будет меньше, чем на зажимах генератора, так как в линии будет потеря напряжения. По формуле
ΔU = 1⋅r = 50⋅0,1 = 5 в.
Если в линии потеря напряжения равна 5 в, то напряжение у электродвигателя будет 115 - 5 = 110 в.
Пример 14. Напряжение на зажимах генератора равно 240 в. Электроэнергия по линии из двух медных проводов длиной по 350 м, сечением 10 мм2 передается к электродвигателю, потребляющему ток в 15 а. Требуется определить напряжение на зажимах двигателя.
Напряжение на зажимах двигателя будет меньше напряжения генератора на величину потери напряжения в линии.
Так как сопротивление r проводов неизвестно, определяем его по формуле
| r = 2 | ρ⋅l | = 2⋅ | 0,0175⋅350 | = 1,22 ом. |
| S | 10 |
Подставляя r в формулу, получим
ΔU = I⋅r = 15⋅1,22 = 18,3 в.
Следовательно, напряжение на зажимах двигателя будет 240 - 18,3 = 221,7 в.
Пример 15. Определить поперечное сечение алюминиевых проводов, которое необходимо применить, чтобы передать электрическую энергию двигателю, работающему при напряжении в 120 в и токе в 20 а. Энергия к двигателю будет подаваться от генератора напряжением 127 в по линии длиной 150 м.
Находим допустимую потерю напряжения:
ΔU = 127 - 120 = 7 в.
Сопротивление проводов линии должно быть равно:
r = ΔU/I = 7/20 = 0,35 ом.
Из формулы
r = 2 ρ⋅l/S
определяем сечение провода:
| S = 2 | ρ⋅l | = | 0,03⋅300 | = 25,7 мм2. |
| r | 0,35 |
По справочнику выбираем имеющееся сечение 25 мм2.
Если ту же линию выполнить медным проводом, то сечение его будет равно:
| S = 2 | ρ⋅l | = | 0,0175⋅300 | = 15 мм2. |
| r | 0,35 |
Выбираем сечение 16 мм2.
Пример 16. Для устойчивого горения электрической дуги требуется ток 10 а при напряжении 40 в. Определить величину добавочного сопротивления, которое нужно включить последовательно с дуговой установкой, чтобы питать ее от сети с напряжением 120 в.
Падение напряжения в добавочном сопротивлении составит
120 - 40 = 80 в.
Зная падение напряжения в добавочном сопротивлении и ток, протекающий через него, можно по закону Ома для участка цепи определить величину этого сопротивления:
| r = | U | = | 80 | = 8 ом. |
| I | 10 |
При рассмотрении электрической цепи мы до сих пор не принимали в расчет того, что путь тока проходит не только по внешней части цепи, но также и по внутренней части цепи, т. е. внутри самого элемента, аккумулятора или другого источника энергии.
Электрический ток, проходя по внутренней части цепи, преодолевает ее внутреннее сопротивление и потому внутри источника также происходит падение напряжения.
Следовательно, электродвижущая сила (э.д.с.) источника электрической энергии идет на покрытие внутренних и внешних потерь напряжения в цепи.
Если Е - электродвижущая сила в вольтах, I - ток в амперах, r - сопротивление внешней цепи в омах, r0 - сопротивление внутренней части цепи в омах, ΔU0 - внутренняя потеря напряжения и U - напряжение внешней цепи, то
E = ΔU0 + U = Ir0 + Ir = I(r0 +r),
| I = | E | . |
| r0 + r |
Это есть формула закона Ома для всей цепи. Словами она читается так: ток в электрической цепи равен электродвижущей силе, деленной на сопротивление всей цепи (сумму внутреннего и внешнего сопротивлений).
Пример 17. Электродвижущая сила Е элемента равна 1,5 в, его внутреннее сопротивление r0 = 0,3 ом. Элемент замкнут на сопротивление r = 2,7 ом.
Определить ток в цепи:
| I = | E | = | 1,5 | = 0,5 a. |
| r0 + r | 0,3 + 2,7 |
Пример 18. Определить э.д.с. элемента Е, замкнутого на сопротивление r = 2 ом, если ток в цепи I = 0,6 а. Внутреннее сопротивление элемента r0 = 0,5 ом.
Вольтметр, включенный на зажимы элемента, покажет напряжение на них, равное напряжению сети или потере напряжения во внешней цепи:
U = I⋅r = 0,6⋅2 = 1,2 в.
Следовательно, часть э.д.с. элемента идет на покрытие внутренней потерн напряжения, а остальная часть - 1,2 в - отдается в сеть.
Внутреннее падение напряжения
ΔU0 = I⋅r0 = 0,6⋅0,5 = 0,3 в.
Так как Е = ΔU0 + U, то
E = 0,3 + 1,2 = 1,5 в.
Тот же ответ можно получить, если воспользоваться формулой закона Ома для всей цепи
| I = | E | , |
| r0 + r |
откуда
Е = I(r0 + r) = 0,6(0,5 + 2) = 1,5 в.
При размыкании электрической цепи ток по ней проходить не будет. Ток не будет проходить также и внутри источника э.д.с., а следовательно, не будет и внутренней потери напряжения. Поэтому вольтметр при разомкнутой цепи покажет э.д.с. источника электрической энергии.
Таким образом, вольтметр, включенный на зажимы источника э.д.с., показывает:
при замкнутой электрической цепи - напряжение сети;
при разомкнутой электрической цепи - э.д.с. источника электрической энергии.
Пример 19. Электродвижущая сила элемента 1,8 в. Он замкнут на сопротивление r = 2,7 ом. Ток в цепи равен 0,5 а. Определить внутреннее сопротивление r0 элемента и внутреннее падение напряжения ΔU0:
r0 + r = E/I = 1,8/0,5 = 3,6 ом.
Так как r = 2,7, то
r0 = 3,6 - 2,7 = 0,9 ом;
ΔU0 = I⋅r0 = 0,5⋅0,9 = 0,45 в.
Из решенных примеров видно, что показание вольтметра, включенного на зажимы источника э.д.с., не остается постоянным при различных условиях работы электрической цепи. При увеличении тока в цепи увеличивается также внутренняя потеря напряжения; поэтому при неизменной э.д.с. на долю внешней сети будет приходиться все меньшее и меньшее напряжение.
В табл. 6 показано, как меняются ток в цепи и напряжение на зажимах U в зависимости от изменения внешнего сопротивления (r) при неизменных э.д.с. (Е) и внутреннем сопротивлении (r0) источника энергии
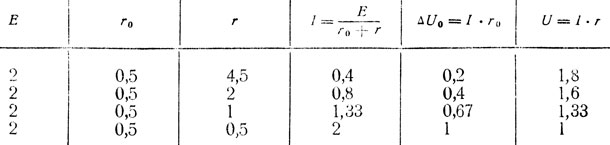
Таблица 6. Зависимость тока в цепи и напряжения от сопротивления r при неизменных э.д.с. и внутреннем сопротивлении r0
На рис. 25 приведена зависимость напряжения U на зажимах цепи от величины нагрузочного тока I.
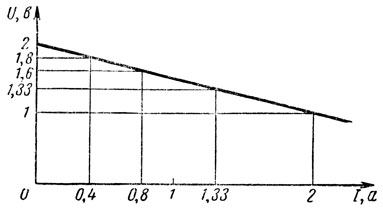
Рис. 25. Зависимость напряжения на зажимах цепи от величины тока нагрузки

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
