§ 12. Соединение проводников между собой. Первый закон Кирхгофа

Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно.

Если проводники соединены таким образом, что по ним проходит один и тот же ток, то такое соединение проводников называется последовательным (рис. 26).

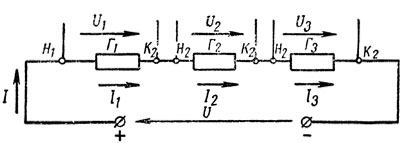
Рис. 26. Последовательное соединение проводников

Следовательно, ток на отдельных участках последовательной цепи имеет одинаковую величину:

Сумма падений напряжений на отдельных участках равна напряжению всей цепи:

Напряжение цепи можно представить как

где r - общее сопротивление всей цепи.

Следовательно,

Сокращая обе части равенства на I, получим

Общее сопротивление цепи, состоящей из нескольких последовательно соединенных сопротивлений, равно сумме этих сопротивлений.

Пример 20. Три сопротивления 10, 15 и 20 ом соединены последовательно, как показано на рис. 27. Ток в цепи 5 а. Определить падение напряжения на каждом сопротивлении и общее напряжение цепи:

Рис. 27. К примеру 20

Если два или большее число проводников присоединены к двум узловым точкам, то такое соединение проводников называется параллельным (рис. 28). Напряжение на каждом из проводников равно напряжению U, приложенному к узловым точкам цепи А и В.

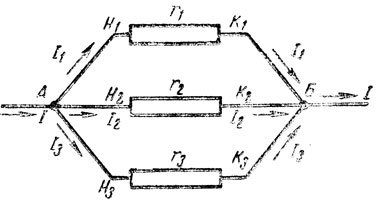
Рис. 28. Параллельное соединение проводников

На рисунке видно, что при параллельном соединений проводников для прохождения тока имеется несколько путей. Ток, притекая к точке разветвления A, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:

Если токи, приходящие к точке разветвления, считать положительными, а уходящие - отрицательными, то для точки разветвления можно написать:

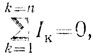
т. е. алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение называется первым законом Кирхгофа.

Обычно при расчете электрических цепей направления токов в ветвях, присоединенных к какой-либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме. Действительные направления токов определятся в результате расчета.

Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей. Общий ток, приходящий к точке F, равен

Токи в каждой из ветвей имеют значения:

По первому закону Кирхгофа,

или

Вынося U в правой части равенства за скобки, получим

Сокращая обе части равенства на U, получим формулу подсчета общей проводимости ¹/_r = ¹/_r1 + ¹/_r2 + ¹/_r3,

или

Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.

Пример 21. Определить общее сопротивление трех параллельно включенных сопротивлений, если r₁ = 2 ом, r₂ = 3 ом, r₃ = 4 ом:

откуда

Пример 22. Пять сопротивлений 20, 30, 15, 40 и 60 ом включены параллельно в сеть. Определить общее сопротивление:

откуда

Следует заметить, что общее сопротивление разветвленного участка цепи всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.

Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r₁, деленному на число ветвей n:

Пример 23. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 ом каждое:

Для проверки попробуем найти сопротивление разветвления по формуле

откуда

Как видим, ответ получается тот же.

Пример 24. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рис. 29, а.

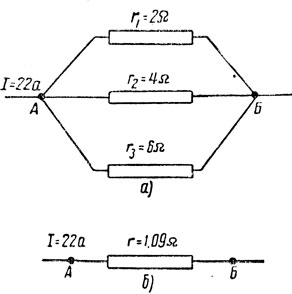
Рис. 29. К примеру 24

Найдем общее сопротивление цепи:

откуда

Теперь все разветвление мы можем изобразить упрощенно как одно сопротивление (рис. 29, б).

Падение напряжения на участке между точками A и Б будет

Возвращаясь снова к рис. 28, а, видим, что все три сопротивления окажутся под напряжением 24 в, так как они включены между точками A и Б. Рассматривая первую ветвь разветвления с сопротивлением r, мы видим, что напряжение на этом участке 24 в, сопротивление участка 2 ом. По закону Ома, ток на этом участке будет

Ток второй ветви

Ток третьей ветви

Проверим по первому закону Кирхгофа:

Следовательно, задача решена верно.

Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения:

первая ветвь: r1 = 2 ом, I1 = 12 а; 
вторая ветвь: r2 = 4 ом, I2 = 6 а; 
третья ветвь: r3 = 6 ом, I3 = 4 а.

Как видим, сопротивление первой ветви в два раза меньше сопротивления второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.

Для двух параллельных ветвей проще пользоваться данной выше формулой.

Общее сопротивление в этом случае можно подсчитать по формуле

или окончательно:

Если в электрической цепи имеются как последовательные, так и параллельные соединения отдельных проводников, то мы имеем дело со смешанным соединением.

Пример 25. Определить общее сопротивление смешанного соединения, представленного на рис. 30, если

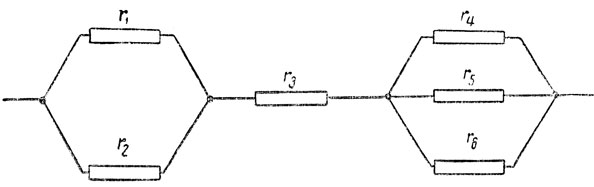
Рис. 30. Смешанное соединение проводников

Находим общее сопротивление первого разветвления:

откуда

Общее сопротивление второго разветвления

откуда

Общее сопротивление цепи