
§ 15. Второй закон Кирхгофа. Применение законов Кирхгофа для расчета электрических цепей
При расчете электрических цепей часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы.
На рис. 35 представлена часть сложной электрической цепи в виде замкнутого контура АБВГ. На схеме указаны полярность электродвижущих сил E1, E2, E3 и направления токов I1, I2, I3 и I4, протекающих на различных участках цепи.
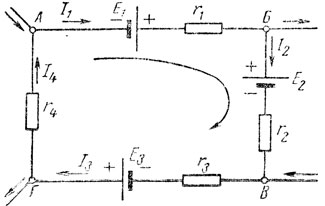
Рис. 35. Участок сложной электрической цепи
Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим каждый из участков рассматриваемого контура. На первом участке разность потенциалов между точками А и Б, или, что то же самое, напряжение UAБ, равна э.д.с. Е1 минус падение напряжения I1r1. Аналогично будет и на других участках цепи:
на участке АБ φА - φБ = Е1 - I1r1; на участке БВ φБ - φВ = -Е2 - I2r2; на участке ВГ φВ - φГ = E3 - I3r3; на участке ГА φГ - φА = I4r4.
Складывая левые и правые части уравнения, получим:
φA - φБ + φБ - φВ + φВ - φГ + φГ - φА = E1 - I1r1 - E2 - I2r2 + E3 I3r3 + I4r4;
0 = E1 - I1r1 - E2 - I2r2 + E3 - I3r3 + I4r4.
Перенося произведения (I⋅r) в одну часть, а электродвижущие силы (Е) в другую часть, получим
-E1 + E2 - E3 = - I1r1 - I2r2 - I3r3 + I4r4.
Или в общем виде
ΣE = ∑I ⋅ r.
Это выражение представляет собой второй закон Кирхгофа. Формула показывает, что во всяком замкнутом контуре алгебраическая сумма электродвижущих сил равна алгебраической сумме падений напряжений.
По второму закону Кирхгофа,
∑E = ∑Ir.
Для простейшей замкнутой цепи с одной э.д.с. Е (рис. 36)
E = Ir0 + Ir = I(r0 + r),
откуда
I = E/r0+r.
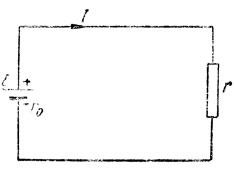
Рис. 36. Простой замкнутый контур
Мы получили формулу закона Ома для замкнутой цепи.
Следовательно, закон Ома является частным случаем 2-го закона Кирхгофа.
При расчете электрических цепей применяют различные методы расчета. Выбор того или иного метода зависит от конфигурации цепи, числа э.д.с., заданных величин.
Как правило, расчет неразветвленных цепей с любым числом э.д.с., а также расчет сложных цепей с одной э.д.с. легче производить, применяя закон Ома.
Расчет сложных цепей с несколькими э.д.с. производят с помощью уравнений 1-го и 2-го законов Кирхгофа.
Расчет сложной цепи методом законов Кирхгофа производят в следующем порядке:
Условно задаются направлениями токов в различных участках цепи.
Определяют число уравнений, которое необходимо составить для решения задачи. Если известны все э.д.с. и сопротивления цепи, число уравнений должно быть равно числу неизвестных токов.
Для составления уравнений вначале используют уравнения 1-го закона Кирхгофа. Число уравнений 1-го закона Кирхгофа на единицу меньше числа узловых точек в схеме. Остальное число уравнений составляют по 2-му закону Кирхгофа.
Для этого намечают контуры, направление обхода этих контуров и приступают к составлению уравнений. Если направление обхода не совпадает с направлениями э.д.с. или с направлениями токов на отдельных участках контура, то величины э.д.с. и падения напряжения I⋅r входят в уравнения со знаком минус.
Решая систему уравнений, находят величину токов,
Если окажется, что в результате решения уравнений некоторые из токов получились отрицательными, то это значит, что направление этих токов было выбрано неправильно. Надо изменить направление токов на схеме.
Проверка правильности решения производится путем подстановки полученных значений токов в одно из составленных уравнений.
Решим несколько задач, используя закон Ома и оба закона Кирхгофа.
Пример 30. Найти токи в цепи, представленной на рис. 37. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:
-E1 + E2 = Ir1 + Ir2;
-1,9 + 1,3 = I(2 + 3);
-0,6 = 5I, I = -0,12 а.
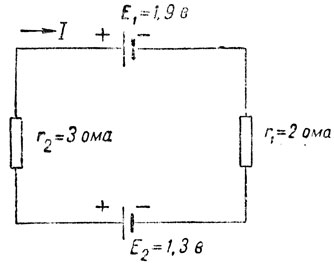
Рис. 37. Электрическая цепь (к примеру 30)
Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Пример 31. Дана электрическая цепь (рис. 38). Определить токи на отдельных участках.
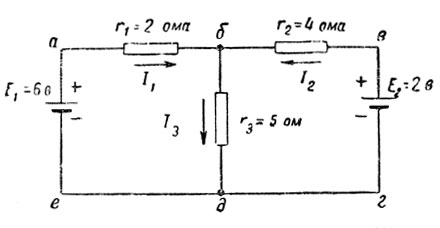
Рис. 38. Электрическая цепь (к примеру 31)
Произвольно выбираем положительные направления токов.
Для контура абде
6 = 2I1 + 5I3. (1)
Для контура авге
6 - 2 = 2I1 - 4I2. (2)
Для точки б, по первому закону Кирхгофа,
I3 = I1 + I2. (3)
Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I3 из уравнения (3) в уравнение (1), получим
6 = 2I1 + 5I1 + 5I2; 6 = 7I1 + 5I2 + 2 = I1 - 2I2
или
12 = 14I1 + 10I2 + 10 = 5I1 + 10I2.
Складывая два последних уравнения, имеем:
22 = 19I1, откуда I1 = 1,156 а,
подставляем значение I1 в уравнение (1):
6 = 2 ⋅ 1,156 + 5I3,
| I3 = | 6 - 2 ⋅ 1,156 | = 0,74 а. |
| 5 |
Подставляем значение I1 в уравнение (2):
2 = 1,156 - 2I2,
откуда
| I2 = | - 2 + 1,156 | = - 0,422 a. |
| 2 |
Знак минус показывает, что действительное направление тока I2 обратно принятому нами направлению.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
