§ 71. Разветвленные цепи переменного тока

Пусть мы имеем векторную диаграмму, изображенную на рис. 159. Проектируя вектор тока I на направление вектора напряжения U, разложим вектор тока на две составляющие.

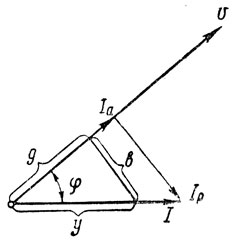
Рис. 159. Разложение тока на активную и реактивную составляющие

Одна из составляющих совпадает по направлению с вектором напряжений и называется активной составляющей тока. Она обозначается буквой I_а и равна

Другая составляющая, перпендикулярная вектору напряжения, называется реактивной составляющей тока. Она обозначается буквой I_р и равна

Таким образом, переменный ток I можно рассматривать как геометрическую сумму двух составляющих: активной I_а и реактивной I_р. Применение этого приема позволяет сравнительно просто производить расчеты разветвленных цепей переменного тока.

Рассмотрим разветвленную цепь, изображенную на рис. 160.

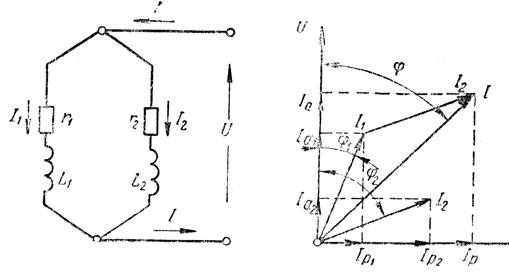
Рис. 160. Параллельное соединение ветвей r₁L₁ и r₂L₂

Токи в ветвях:

Углы сдвига фаз между напряжением и токами в ветвях:

На рис. 160 справа построена векторная диаграмма для параллельного соединения ветвей r₁, L₁ и r₂, L₂. Построение диаграммы начинается с вектора напряжения, так как напряжение является общим для двух ветвей. Ввиду наличия r и L в каждой из ветвей токи I₁ и I₂ отстают по фазе от напряжения U на углы φ₁ и φ₂.

Построив векторы токов I₁ и I₂ и сложив их по правилу параллелограмма, получим вектор тока I, протекающего на общем участке цепи. Из построения диаграммы видно, что

Общий ток равен

Порядок расчета разветвленной цепи покажем на числовом примере.

Пример 11. Для цепи, показанной на рис. 160, дано:

Напряжение сети 127 в, частота 50 гц.

Определить токи в ветвях и на общем участке цепи.

Решение.

Для определения общего тока предварительно находим активные и реактивные составляющие токов:

Рассмотрим параллельное соединение ветвей, содержащих I и С (рис. 161, а):

Рис. 161. Параллельное соединение ветвей L и С

полные сопротивления ветвей будут:

токи ветвей:

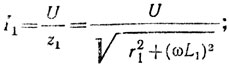
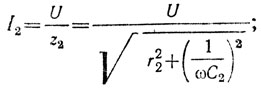
углы сдвига фаз между напряжением и токами в ветвях:

Векторная диаграмма, показанная на том же чертеже б, начинается с построения вектора напряжения U. Затем под углами φ₁ и φ₂ строятся векторы токов I₁ и I₂. Следует заметить, что ток I₁ в ветви с индуктивностью отстает по фазе от напряжения на угол φ₁, а ток I₂ в цепи с емкостью опережает по фазе напряжение на угол φ₂. Складывая векторы токов I₁ и I₂ по правилу параллелограмма, получаем вектор тока I.

Из построения векторной диаграммы видно, что активная составляющая общего тока равна сумме активных составляющих токов в обеих ветвях:

Реактивная составляющая общего тока равна разности реактивных составляющих - индуктивной I_р1 и емкостной I_р2:

Общий ток

Пример 12. Для цепи, представленной на рис. 161, дано: r₁ = 5 ом, L₁ = 0,05 гн, r₂ = 5 ом, С₂ = 100 мкф. Напряжение сети 220 в, частота 50 гц. Найти токи в ветвях и на общем участке цепи.

Решение.