Глава 2. Сообщения, сигналы, помехи

2.1. Сообщения, сигналы и помехи как случайные процессы

Как отмечалось в § 1.1, детерминированное, т. е. заранее известное сообщение не содержит информации. Поэтому в теории связи источник сообщения следует рассматривать как устройство,, осуществляющее выбор из некоторого множества возможных сообщений. Каждая конкретная реализация сообщения возникает с определенной вероятностью, которая в общем случае зависит от того, какие сообщения передавались раньше. Точно так же и посылаемая в канал реализация сигнала является элементом некоторого множества, выбираемого с определенной вероятностью. Множество, на котором задана вероятностная мера, называют ансамблем. Ансамбли сообщений и сигналов могут быть конечными (в дискретном случае) или бесконечными.

Ансамбль {X(t)} функций времени является случайным процессом. Каждая входящая функция x_r(t) называется выборочной функцией или реализацией процесса. Наличие различных реализаций позволяет сигналу переносить информацию. Для этого нужно установить соответствие между каждым сообщением из ансамбля сообщений и определенной реализацией сигнала. Тогда по принятой реализации сигнала можно судить о том, какое сообщение передавалось. Это суждение было бы точным, если бы переданный сигнал не искажался помехами. В действительности помехи являются также случайными процессами, и поэтому по принятому сигналу можно лишь с некоторой вероятностью определить, какое сообщение было передано.

Итак, сообщения, сигналы, помехи являются случайными процессами и для их исследования необходимо использовать основные положения теории случайных процессов (случайных функций). Все содержание данной главы относится в равной степени к случайным сообщениям, сигналам и помехам

Случайный процесс может быть задан на дискретном множестве значений t₁, t₂, ..., t_k. Это случай сообщения (сигнала), дискретного по времени. Такие случайные процессы называются также случайными последовательностями. Примером случайной последовательности является процесс X(t_k), заданный на дискретных точках t₁, t₂ ..., t_k, ... и принимающий в каждой из них значение 1 с вероятностью р₁ и 0 с вероятностью р₀ = 1 - p₁ независимо от значений в других точках. Чаще встречаются процессы, непрерывные по времени, например, заданные на всей оси -∞<t<∞ или на конечном отрезке 0<t<π -T/2<t<T/2 и т. п. Процессы, заданные на конечном отрезке времени, называют финитными.

Задать детерминированную (т. е. не случайную) функцию времени - это значит указать ее значение для любого t в пределах области определения. Случайную функцию можно задать только в вероятностном смысле. Если число реализаций конечно или счетно, можно их просто перечислить и указать их вероятности.

Рассмотрим, как задаются дискретные случайные последовательности элементов A (t_k), могущие принимать m различных значений а₁, а₂, ..., а_m. Реализацией такой последовательности может быть, например, A(t₁) = а₄⁽¹⁾; A(t₂) = а₆⁽²⁾; A(t₃) = a₁⁽³⁾, ... ..., A (t_k) = a_ik^k ; ..., где нижний индекс обозначает значение элемента, а верхний - момент времени. Отрезок такой последовательности длиной n (т. е. состоящий из n элементов) характеризуется своей вероятностью Р. На основании теоремы умножения вероятностей можно в общем случае записать вероятность отрезка реализации, в которой элементы A (tk) принимают значения a_ik (i_k = 1, 2, ..., m) так:

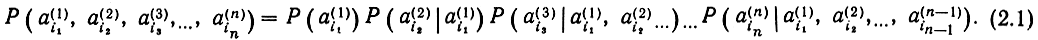
Здесь

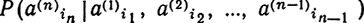
условная вероятность появления элемента а_in в момент i_n при условии, что в предыдущие моменты осуществлялась реализация отрезка

Примером такой последовательности может служить последовательность букв, передаваемых по телеграфу. Хотя для этого случая определить вероятность отрезка нелегко, но качественно сравнить вероятности различных отрезков можно без особого труда. Так, при n = 7 последовательность букв "ВЫЕЗЖАЮ" более вероятна, чем последовательность "ГРАНАТА", которая, в свою очередь, вероятнее, чем последовательность "МАФТУЗА". Последняя все же вероятнее, чем последовательность "АЬМШЗЮО", для которой вероятность появления в осмысленном русском тексте равна нулю. На этом примере, между прочим, легко убедиться, что условная вероятность появления некоторой буквы зависит от ранее переданных букв.

Простейший вид случайной последовательности элементов отличается тем, что появление того или иного элемента не зависит от предыдущих элементов. Для такой последовательности независимых элементов (или последовательности Бернулли)

Важным видом случайной последовательности зависимых элементов является цепь Маркова. Простой цепью Маркова называется последовательность, в которой условная вероятность появления некоторого элемента a_ik целиком определена, если известен предыдущий элемент a_i,k-1 Это значит, что

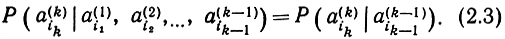
Таким образом, в простой цепи Маркова связь между последовательными элементами целиком определяется зависимостью между соседними элементами. Для вычисления вероятности некоторого отрезка цепи Маркова достаточно знать переходные вероятности, т. е. все условные вероятности P(a_i|a_j) появления элемента a_i, если предыдущим элементом был a_j. Заметим, что это вовсе не означает независимости a^(k)_ik от a^(k-2)_ik-2 или от еще более ранних элементов. Поскольку вероятность появления a^(k)_ik зависит от того, каким был элемент a^(k-1)_ik-1, а последний зависит от то имеет место и зависимость a^(k)_ik от a^k-2_ik-2 если a^(k-1)_ik-1 значение неизвестно. Нетрудно показать, что

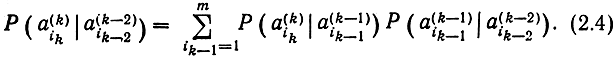
Обобщением простой цепи Маркова является сложная марковская цепь r-го порядка, в которой вероятность элемента целиком определена, если известны r предшествующих ему элементов: марковская цепь высокого порядка является удовлетворительной математической моделью текстовых последовательностей в приведенном выше примере.

Непрерывные случайные функции также могут иметь конечное число реализаций на конечном интервале времени. Для их задания также достаточно указать их вероятности.

Так, например, процесс X(t), заданный на интервале 0≤t≤T и имеющий

Две реализации:

возникающие с вероятностями P(x₁) = p₁, Р(х₂) = p₂ = 1 - p₁, где A, ω₁, ω₂, p₁ - определенные постоянные, является простым примером случайного процесса с конечным числом реализаций. Он может служить сигналом, информационное содержание которого определяется значением частоты ω.

Примером процесса, заданного на том же интервале и имеющего бесконечное число реализаций, может служить процесс

где A и ω - постоянные неслучайные величины, а Φ - случайная величина с заданным распределением вероятностей. Такой процесс может иметь счетное число реализаций (например, если Φ принимает значения φ_k = 2π/k с вероятностями 2^-k) или несчетное (например, если величина Φ равномерно распределена на интервале 0-2π). Довольно часто приходится рассматривать процессы, определенные рядом

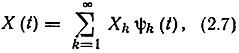
где ψ_k(t) - обычные (детерминированные) функции, а Х_k - случайные величины с заданным распределением вероятности. Сходимость ряда понимается в среднеквадратическом смысле, т. е. при всех :t

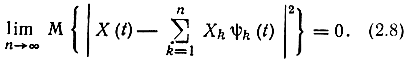
Символ М{ } здесь и в дальнейшем обозначает математическое ожидание.

В общем случае скалярный случайный процесс X (t) полностью задан, если для любого набора моментов времени t₁, t₂, ..., t_n и любых значений x₁, х₂, .., х_n можно вычислить вероятность того, что X(t) принимает в указанные моменты времени значения, не превышающие соответственно x₁, x₂, ...., x_n:

Здесь P{ } обозначает совместную вероятность событий, записанных в скобках. Заметим, что X(t_k) представляет собой случайную величину и называется сечением случайного процесса в момент

Функция F (х₁, x₂, ...., x_n, t₁, t₂, ..., t_n) в (2.9) называется n-мерной функцией распределения вероятности процесса. Ее аргументами являются x₁, x₂ ,..., х_n. Величины t₁, t₂, ..., t_n играют роль параметров. Следует подчеркнуть, что случайный процесс полностью задан в том случае, если для любого n и любых моментов t₁, t₂,..., t_n (в области его определения) можно найти функцию распределения.

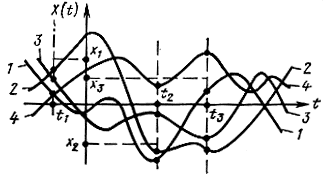
Рис. 2.1. Реализация случайного процесса

На рис. 2.1 представлены четыре реализации некоторого случайного процесса и показаны три его сечения. Реализации 1 к 2 удовлетворяют условиям X(t₁≤x₁), X(t₂) ≤x₂, X(t₃)≤x₃, где х₁, х₂, x₃ - значения сечений, отмеченные на рисунке точками, а реализации 3 и 4 этому условию не удовлетворяют. Если других реализаций данный процесс не имеет, то трехмерная функция распределения при заданных сечениях х₁, х₂, x₃ равна сумме вероятностей реализаций 1 и 2.

Если существуют частные производные функции распределения по всем х_k, то можно определить n-мерную плотность распределения вероятности:

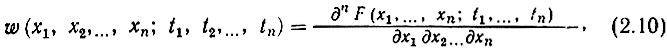
которая также полностью определяет процесс, если она известна для любого числа любых сечений^*.

^* (С помощью обобщенной функции δ (x) можно распространить понятие плотности распределения и на случай разрывной функции распределения. Как известно, если функция F(x) при некотором значении х = х₀ совершает скачок на величину а, то в ее производную войдет слагаемое аδ(х - х₀). Функция δ(х) Равна бесконечности при х₂ = 0 и равна нулю при прочих значениях х, причем ПРИ x₂>x₁)

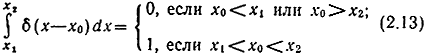
Пусть, например,

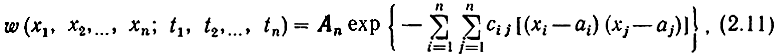
где A_n, c_ij, a_i, a_j - постоянные определенные выбором сечений t₁,...., t_n и связанные между собой некоторыми зависимостями, на которых сейчас останавливаться не будем. В частности, при n = 1 одномерную плотность распределения можно записать следующим образом:

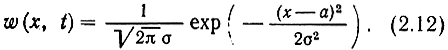
Здесь

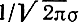
соответствует коэффициенту А₁, а 1/2σ² - коэффициенту с₁₁ в (2.11).

Процесс, у которого любая n-мерная плотность распределения вероятностей выражается (2.11), называется нормальным, или гауссовским. Нормальные процессы играют исключительно важную роль в теории передачи сигналов. Так, в § 1.3 говорилось, что флуктуационные помехи, в частности, вызванные тепловым движением электронов, являются нормальными. Из центральной предельной теоремы вероятности известно, что при некоторых ограничениях сумм большого числа разных процессов образует процесс, очень близкий к гауссовскому.

Среднее значение процесса по ансамблю или его математическое ожидание определяется как

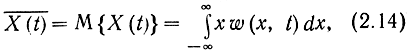
где ω(x, t) - одномерная плотность распределения для сечения t. Математическое ожидание, вообще говоря, является функцией времени (не случайной). Разность между случайным процессом и его математическим ожиданием называется центрированным процессом и обозначается

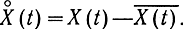
Математическое ожидание квадрата центрированного процесса называется дисперсией:

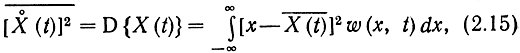
которая, вообще говоря, тоже является функцией времени.

Функция корреляции В_х(t₁, t₂) определяется как математическое ожидание произведения двух сечений центрированного случайного процесса:

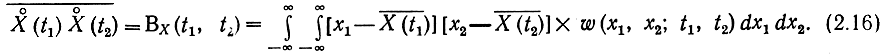
Функция корреляции (ФК), вообще говоря, является функцией двух моментов времени t₁ и t₂. Ее следует отличать от функции взаимной корреляции между двумя процессами X (t) и Y (t):

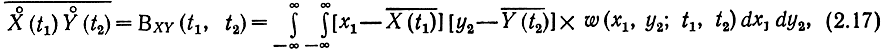
где w(x₁, y₂; t₁, t₂) - двумерная (совместная) плотность вероятности сечения t₁ процесса X и сечения t₂ процесса Y. Иногда функцию корреляции и взаимной корреляции определяют без центрирования.

Легко показать, что для нормального процесса с одномерной плотностью (2.13) математическое ожидание равно a, а дисперсия σ².

Случайный процесс, у которого математическое ожидание и дисперсия не зависит от времени, а ФК зависит от разности t₂ - t₁ = τ, но не от самих значений t₁ и t₂, называется стационарным (в широком смысле)^*. Реальные сообщения, сигналы и помехи обычно не являются стационарными. Однако если их рассматривать на протяжении не слишком длительного времени, то с хорошим приближением их можно описать стационарными процессами, которые поэтому широко используются в качестве математической модели реальных сообщений, сигналов и помех.

^* (Стационарными в узком смысле называются процессы, у которых любые n-мерные функции распределения (2.2) не изменяются, если все моменты времени t₁, ..., t_n сдвинуть на любой интервал τ. Очевидно, что процесс, стационарный в узком смысле, является стационарным и в широком смысле. Обратное утверждение неверно. В настоящей книге стационарность понимается всегда в широком смысле.)

Примером стационарного процесса может служить процесс (2.6), если Φ - случайная величина, распределенная равномерно на интервале (0; 2π). Его математическое ожидание равно нулю, дисперсия равна 0,5A², а функция корреляции

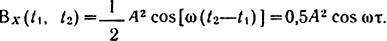
Наоборот, процесс (2.5) стационарным не является.

Помимо средних значений по ансамблю можно определить средние значения случайного процесса по времени. Для финитного процесса, заданного на интервале времени от t₁ до t₂, определим постоянную составляющую:

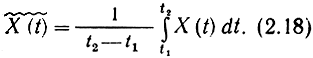
Если процесс задан на бесконечной оси времени, то для него постоянная составляющая

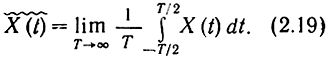
Постоянная составляющая, очевидно, сама от времени не зависит, но является, вообще говоря, случайной величиной - ее значение зависит от реализации сигнала.

Процесс

называется переменной составляющей процесса X(t). Среднее по времени значение квадрата переменной составляющей

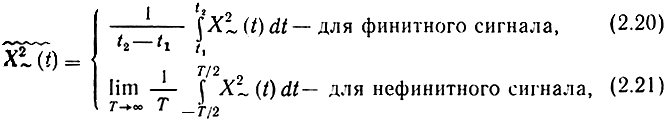
процессы часто используют в качестве математических моделей реальных сообщений, сигналов и помех.

Функцию корреляции эргодического процесса также можно вычислить по одной реализации усреднением по времени:

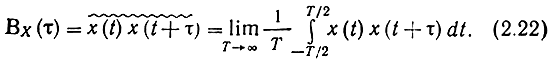
Рассмотрим некоторые свойства функции корреляции стационарного случайного процесса В_х(τ), где τ - разность между двумя сечениями. С учетом стационарности можно записать:

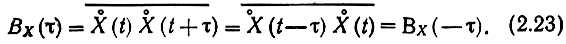
Таким образом, ФК стационарного процесса является четной функцией интервала τ. При τ = 0

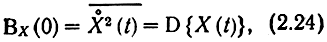
т. е. значение корреляционной функции в точке τ = 0 равно дисперсии сигнала.

В теории вероятностей доказывается, что при любом

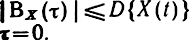
Таким образом, В_х(τ) имеет максимум при τ = 0.

Определим нормированную функцию корреляции (НФК) или коэффициент корреляции процесса Х(t) как

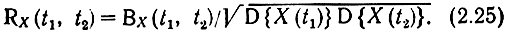
В частности, для стационарного процесса

Из свойств функции корреляции следует, что для стационарного процесса

Величина R_x(τ) является в известной степени мерой статистической зависимости между сечениями процесса, отстоящими на интервал τ. Действительно, если при некотором значении τ X(t) и X(t+τ) всегда совпадают, то, как легко убедиться, R(τ) = 1. Если при другом значении τ X(t) = -X(t+τ), то R(t) = - 1. Если, наконец, X(t) и X(t+τ)-независимые случайные величины, то

откуда и

Таким образом, независимые сечения являются также некоррелированными. Обратное утверждение в общем случае неверно - два сечения могут быть некоррелированными и в то же время зависимыми. Только в том случае, когда процесс гауссовский, из некоррелированности двух сечений следует их независимость.

Коэффициент и функция корреляции для эргодических случайных процессов стремятся к нулю с увеличением τ. Это происходит потому, что чем дальше отстоят друг от друга сечения, тем слабее статистическая зависимость между ними. Интервал времени τ_k называется временем корреляции процесса, если при τ>τ_k величина |R(х)| становится пренебрежимо малой (практически в большинстве случаев для этого достаточно, чтобы она стала меньше 0,1). Иногда интервал корреляции определяют как основание прямоугольника с высотой, равной 1, площадь которого равна площади, ограниченной кривой |R(τ)| и осями координат:

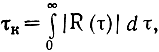
если этот интеграл существует.

Многомерные функции и плотности распределения (2.9), (2.10) иногда удобнее выражать через условные функции (плотности) распределения, аналогично" тому, как это было сделано для вероятностей отрезка последовательности (2.1).. Особенно удобно такое представление для марковских процессов, которые являются аналогом простых марковских цепей и обладают тем свойством, что при известном значении X(t_k-1) = x_k-1 вероятность значения X(t_k) (t_k>t_k-1) не зависит от значений в любые более ранние моменты времени:

Отсюда следует, что для марковского процесса при t₁<t₂<... <t_n

Теория марковских процессов хорошо разработана и широко используется в современной теории связи. В частности, при некоторых дополнительных условиях переходная плотность вероятности w(x₂; t₂|x₁; t₁), где t₂>t₁ удовлетворяет дифференциальному уравнению 2-го порядка в частных производных:.

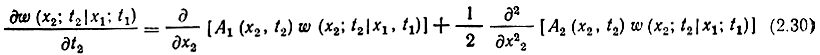
при начальном условии w₁(x₂; t₁|x₁; t₁) = δ(х₂ - x₁). Здесь A₁(x₂, t₂) - коэффициент сноса, а А₂(х₂, t₂) -коэффициент диффузии.

Уравнение (2.30) называют уравнением Колмогорова-Фоккера-Планка. Марковские процессы, удовлетворяющие этому уравнению, называют диффузионными. В общем случае это нестационарные процессы. Для стационарного процесса коэффициенты А₁ и A₂ не зависят от t₂.

В зависимости от вида коэффициентов A₁ и A₂ диффузионный марковский процесс может иметь различные распределения вероятностей. В частности, он может быть гауссовским. Имеет место следующая теорема: чтобы стационарный гауссовский процесс был марковским, необходимо и достаточно, чтобы его коэффициент корреляции был экспоненциальным:

где α - постоянная.