2.2. Спектры случайных процессов

При изучении различных преобразований детерминированных непериодических сигналов, в частности, прохождения их через линейные цепи широко используют спектральное представление с помощью преобразования Фурье. Напомним, что преобразованием Фурье от x(t) является комплексная функция от частоты f, обозначаемая обычно S(iω) или S(i2πf) и равная

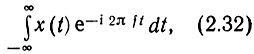
если этот интеграл существует.

При изучении случайных сигналов и помех желательно определить спектр, характеризующий не отдельную выборочную функцию, а весь ансамбль в целом. При попытке применить преобразование Фурье (2.32) к случайным процессам возникают различные препятствия, а именно:

Как известно, для существования интеграла (2.32) необходимо, чтобы функция x(t) была абсолютно интегрируема или хотя бы интегрируема в квадрате^*. Последнее означает, что интеграл

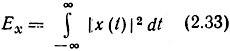
должен сходиться. Заметим, что интеграл (2.33) представляет собой энергию сигнала (при обычном предположении, что через единичное сопротивление проходит ток х(t) или к нему приложено напряжение x(t)). Таким образом, преобразование Фурье существует для сигналов с конечной энергией. Но в случае стационарных эргодических процессов каждая выборочная функция с вероятностью 1 имеет бесконечную энергию. Это следует из того, что такой процесс имеет положительную среднюю мощность, равную его дисперсии, а задан он на бесконечной оси времени. Следовательно, преобразование (2.32) для него не существует.

^* (В этом случае преобразование Фурье существует в смысле среднеквадратической сходимости.)

2. Для тех процессов, которые имеют конечную энергию (а это нестационарные процессы)^*, можно определить преобразование Фурье как случайную комплексную функцию частоты:

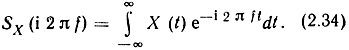
^* (Множество функций с конечной энергией называют "пространством L₂". Об этом будет подробно в 2.5.)

Однако она оказывается почти бесполезной для описания ансамбля. Это вызвано тем, что каждая ее реализация является индивидуальной характеристикой одной конкретной реализации процесса и из нее трудно извлечь данные, характеризующие все множество.

Выход из этих затруднений заключается в отбрасывании некоторых параметров спектра, а именно спектра фаз, и построении функции, характеризующей распределение энергии процесса по оси частот.

Построение такой функции проведем сначала для процессов с конечной энергией, для которых существует случайная спектральная плотность S_X(i2πf) (2.34). Каждая ее реализация соответствует реализации x(t), и для них, согласно теореме Парсеваля,

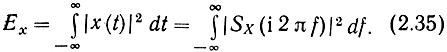
функция |S_X(i2πf)|² характеризует, таким образом, распределение энергии реализации по оси частот. Назовем ее спектральной плотностью энергии реализации.

Усреднив эту функцию по всем реализациям, получим спектральную плотность энергии процесса

Отметим некоторые свойства спектральной плотности энергии. Из ее определения следует, что она неотрицательна. Кривая, изображающая эту функцию, охватывает площадь, равную математическому ожиданию энергии процесса. Она определена на бесконечной оси, т. е. как для положительных, так и отрицательных частот. Как известно из теории преобразования Фурье, для действительной функции x(t) модуль |S_Х(i2πf)| является четной функцией частоты. Поэтому о спектральном распределении энергии процесса можно судить и по одной половине графика функции (2.36), например при f≥0.

Перейдем теперь к стационарному центрированному процессу X(t), реализации которого с вероятностью 1 имеют бесконечную энергию и, следовательно, не имеют преобразования Фурье. Определим усеченный процесс следующим образом:

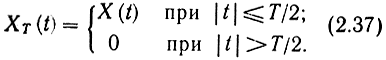
Усеченный процесс имеет конечную энергию, а следовательно, и спектральную плотность энергии,

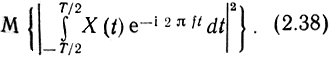
Разделив спектральную плотность энергии усеченного процесса X_T(t) на его длительность T, получим спектральную плотность его мощности

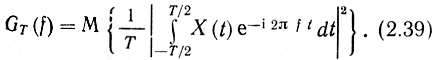
Теперь можно устремить интервал Т к бесконечности и определить спектральную плотность мощности (СПМ) или энергетический спектр (ЭС) стационарного процесса:

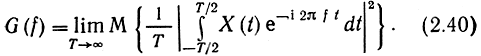
Можно убедиться, что G(f) - неотрицательная четная функция, ограничивающая (вместе с осью абсцисс) площадь, равную мощности

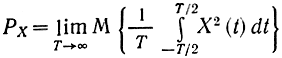
центрированного процесса X(t).

Напомним, что для центрированных эргодических процессов мощность совпадает с дисперсией.

Во многих случаях удобнее пользоваться односторонней спектральной плотностью мощности, заданной при f>0: G₀(f) = 2G(f). Множитель 2 обеспечивает равенство

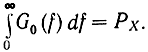
Нормированной спектральной плотностью мощности γ(f) будем называть отношение G(f)/P_X. Отметим, что для любых процессов Х(t) с конечной или бесконечной энергией можно определить нормированный энергетический спектр (НЭС)

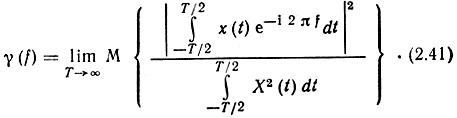
Для процессов из L₂ в (2.41) существуют раздельно пределы числителя (2.36) и знаменателя (2.35), и в этом случае γ(f) представляет нормированную спектральную плотность энергии. Для стационарных процессов пределы числителя и знаменателя порознь не существуют, но, как легко убедиться, предел их отношения совпадает с G(f)/P_x. Таким образом, нормированный энергетический спектр является универсальной характеристикой сигнала. Он характеризует относительное распределение энергии (или мощности) процесса в частотной области. Его график всегда ограничивает площадь, равную 1. В инженерной практике чаще всего под спектром понимают именно нормированный энергетический спектр. Для примера на рис. 2.2 показаны односторонние нормированные энергетические спектры γ₀(f) = 2γ(f) (при f>0) для некоторых ансамблей сигналов.

Часто применяют математические модели сигналов, в которых спектр отличен от нуля только на некоторой полосе частот f₁≤f≤f₂, т. е. процессы с финитным спектром. Разность F = f₂-f₁ является шириной спектра. В реальных условиях жесткого ограничения спектра не бывает и под шириной спектра F понимают ширину минимальной полосы частот, на которой сосредоточена подавляющая часть (обычно 95%) мощности (или энергии) сигнала (см. рис. 2.2).

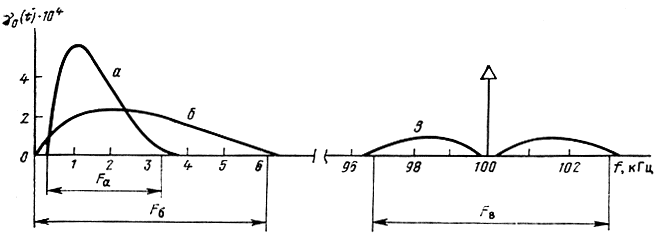
Рис. 2.2. Односторонние нормированные энергетические спектры некоторых сигналов: а - телефонного; б - первичного радиовещательного; в - радиотелефонного при амплитудной модуляции (на несущей частоте 100 кГц сосредоточено 70% мощности)

Спектральную плотность мощности стационарного случайного процесса можно определить по его корреляционной функции на основании следующей теоремы Хинчина - Винера:

Спектральная плотность мощности G(f) центрированного стационарного случайного процесса является преобразованием Фурье от корреляционной функции В_X(τ):

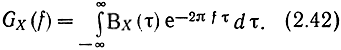
Доказательство этой теоремы можно найти в [11]. Заметим, что это доказательство предполагает абсолютную интегрируемость В(τ). Однако теорему Хинчина-Винера можно успешно применять и в тех случаях, когда В(τ) не удовлетворяет свойству абсолютной интегрируемости, если допустить, что В(τ) и G(f) выражаются через обобщенные функции. Так, например, ФК процесса (2.6), если Ф имеет равномерное распределение на интервале (0; 2π), равна В (τ) = 0,5 А² cos ωτ и не является абсолютно интегрируемой. Однако ее преобразование Фурье G(f) = 0,25A²[δ(2πf-ω)+δ(2πf+ω)] имеет физический смысл. Это линейчатый спектр, сосредоточенный на частотах f = ±ω/2π.

Отметим несколько следствий теоремы Хинчина - Винера.

Следствие 1. Из теории преобразования Фурье следует справедливость обратного преобразования

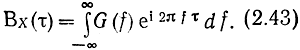
Следствие 2. Значение G(f) на нулевой частоте равно интегралу корреляционной функции. Для доказательства достаточно Сложить в (2.42) f = 0.

Следствие 3. Так как G(f) -неотрицательная функция, то в (2.42) следует, что корреляционными функциями случайных процессов могут быть только такие, которые имеют положительное преобразование Фурье. В частности, например, "прямоугольная" функция

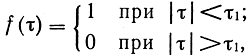
не может быть корреляционной. Функции, имеющие положительное преобразование Фурье, называются положительно определенными.

Формулы (2.42) и (2.43) можно записать более компактно, если учесть, что В_X (τ) так же, как и G(f) являются четными функциями:

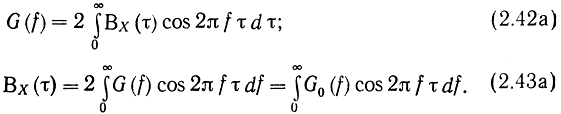
Аналогично можно получить связь между нормированной функцией корреляции R_X(τ) и нормированным энергетическим спектром γ(f):

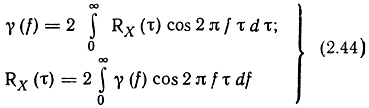
иди для одностороннего спектра

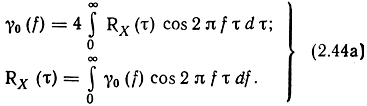
Рассмотрим несколько полезных примеров.

1. Найдем ФК и СПМ "случайного синхронного телеграфного сигнала". Под этим понимается центрированный случайный процесс, принимающий с равной вероятностью значения +1 и -1, причем смена значения может происходить только в моменты времени, разделенные промежутком Т₀ (тактовым интервалом). Значения на разных тактовых интервалах независимы. Пример реализации такого процесса приведен на рис. 2.3. Заметим, что границы тактовых интервалов у разных реализаций не совпадают, так что любой момент времени на интервале 0-Т может с равной вероятностью оказаться моментом начала такта.

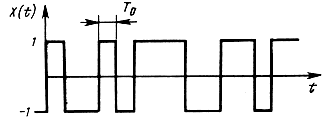
Рис. 2.3. Реализация синхронного телеграфного сигнала

Для определения ФК рассмотрим два сечения в моменты t₁ и t₂, обозначим t₂-t₁ через τ и найдем математическое ожидание произведения X(t₁)X(t₁ + τ).

Если τ>T₀, то эти сечения принадлежат разным тактовым интервалам и произведшие может с равной вероятностью принимать значения +1 и -1, так что его математическое ожидание равно нулю. Бели же τ<T₀, то возможны два случая: случай А, когда они принадлежат одному интервалу и, следовательно, X (t₁)X(t₁+τ) = 1, и случай В, когда они принадлежат разным интервалам и X(t₁)X(t₁ + τ) может с равной вероятностью равняться +1 и -1. Поэтому при τ<T₀ математическое ожидание X(t₁)X(t₁+τ) равно вероятности Р(А) того, что оба сечения оказались в одном интервале. Легко сообразить, что случай А имеет место, если первое из двух сечений отстоит от начала тактового интервала не более чем на T₀ -|τ|, а вероятность этого равна 1-|τ|/T₀. Итак,

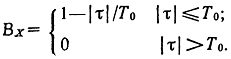
Так как В_Х зависит только от разности t₂-t₁=τ, а

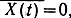
то процесс стационарный. График функции корреляции представлен на рис. 2.4,а.

Спектральную плотность мощности синхронного телеграфного сигнала вычислим по (2.42а):

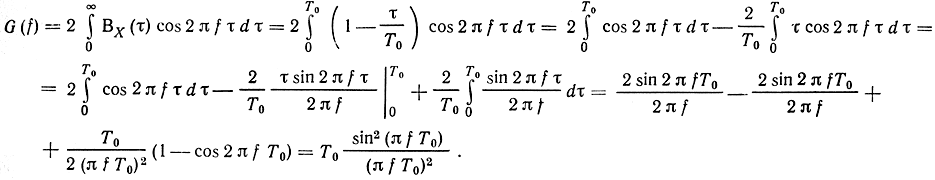
Полученная спектральная плотность показана на рис. 2.4,б. Заметим, что дисперсия рассмотренного сигнала равна 1, поэтому В_X(τ) совпадает с R_X(t), a G(f) - с γ(f).

2. Найдем нормированный энергетический спектр марковского нормального процесса, для которого коэффициент корреляции выражается (2.31). Используя

(2.44), находим

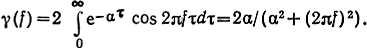
На рис. 2.5 изображены графики функций R(τ) и γ(f).

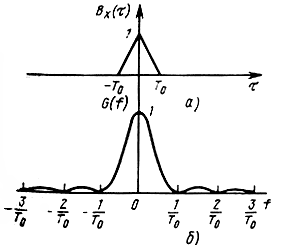
Рис. 2.4. Функция корреляции (а) и спектральная плотность мощности (б) синхронного телеграфного сигнала

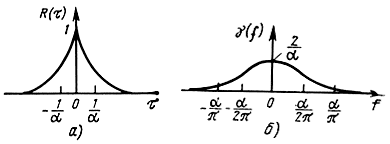
Рис. 2.5. Коэффициент корреляции (а) и нормированный энергетический спектр (б) марковского гауссовского процесса

3. Пусть X (t) - центрированный стационарный случайный процесс со спектральной плотностью мощности G_Y(f). Найдем спектральную плотность мощности G_Y(f) процесса Y(t) = X(t) cos (2πf₀ + Φ), где Φ - случайная величина, не зависящая от X и равномерно распределенная на интервале от 0 до 2π. Такая задача часто встречается при изучении модуляции, когда f₀ - несущая частота, а X(t) - модулирующий первичный сигнал.

Легко убедиться, что процесс Y(t) также центрированный. Начнем с отыскания функции корреляции B_Y(t₁, t₂):

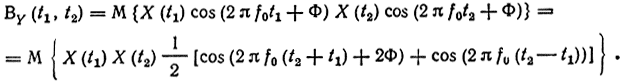
Так как математическое ожидание произведения независимых величин равно произведению их математических ожиданий, получим

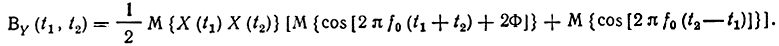
Но

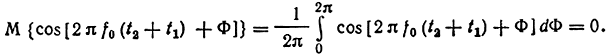
Окончательно

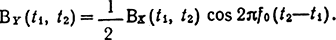
Поскольку X(t) - стационарный процесс, B_X(t₁, t₂) = B_X(t), где τ = t₂-t₁, то и Y(t) оказывается стационарным:

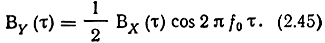
Его спектральная плотность мощности (двусторонняя)

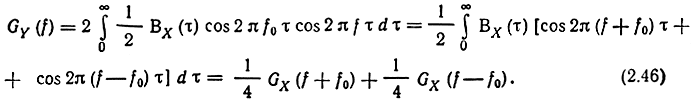
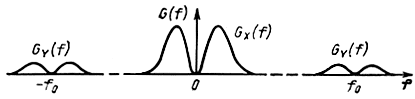
Рис. 2.6. Преобразования спектральной плотности при перемножении процесса на синусоидальную функцию

Иллюстрацией полученного результата является рис. 2.6. Спектр G_Y состоит из двух боковых полос.

Следует отметить, что если бы величина Φ не была случайной или ее распределение вероятностей было несимметричным, то процесс Y(t) не был стационарным.

4. Стационарный процесс W(t) с равномерной спектральной плотностью мощности в некоторой полосе частот называют квазибелым шумом, по аналогии с белым светом, т. е. электромагнитными волнами, имеющими равномерный спектр в области видимых частот. Пусть

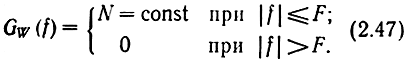
Найдем его корреляционную функцию (рис. 2.7):

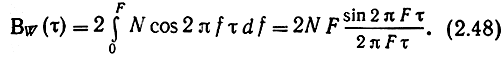
Следует обратить внимание на то, что при значениях τ, кратных 1/(2F), В_W(τ) = 0. Таким образом, сечения процесса, разделенные интервалом k/(2F) (где k - целое число), не коррелированы между собой.

Если беспредельно увеличивать граничную частоту F, то придем к процессу, у которого любые два не совпадающих сечения не коррелированы. Такой процесс называется белым шумом. Его спектральная плотность N постоянна на всех частотах, а ФК

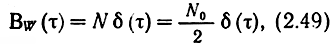
где N₀ = 2N - односторонняя спектральная плотность белого шума, которую называют также интенсивностью шума.

Белый шум представляет собой не реальный физический процесс, а математическую идеализацию, весьма полезную и широко применяемую. Его дисперсия D{W(t)} = B_W(0) = ∞. На практике приходится часто встречаться с процессами, имеющими равномерную спектральную плотность в весьма широкой полосе частот, более широкой, чем полосы пропускания цепей, на которые они воздействуют. Типичным примером является тепловой шум (1.9), имеющий спектральную плотность, которая практически равномерна для частот f<<k(kT/h), что при температуре T = 300 К составляет 6×10¹² Гц. В большинстве случаев замена такого шума идеализированным белым не приводит к погрешности. Белый шум часто используют для определения других случайных процессов. Так, марковский процесс можно задать уравнением (2.16), где N(t) - белый шум.

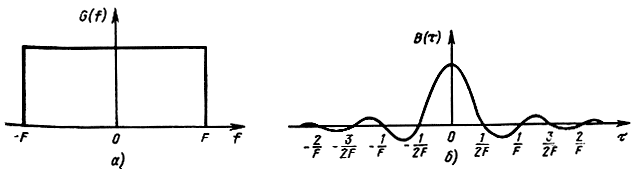
Рис. 2.7. Энергетический спектр низкочастотного квазибелого шума (а), его функция корреляции (б)

Если выделить из белого шума полосу частот (f₁, f₂) (например, пропустив его через идеальный полосовой фильтр), то мощность шума на выходе будет, очевидно, равна N₀ (f₂-f₁).

В некоторых случаях удобно пользоваться идеализированным

нестационарным процессом с ФК

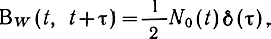
где N₀(t) -некоторая функция времени. Такой процесс называют нестационарным белым шумом.

5. Найдем функцию корреляции высокочастотного квазибелого шума, у которого

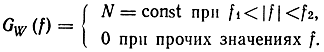
Для него

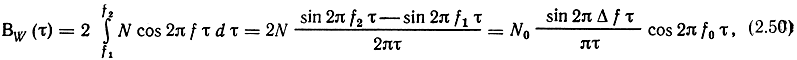
где N₀ = 2N; f₀ = (f₂+f₁)/2; Δf = (f₂-f₁)/2 (рис. 2.8).

Заметим, что полученная корреляционная функция имеет осциллирующий характер благодаря множителю cos 2πf₀Т. Это свойственно всем процессам с относительно узкополосным спектром, ширина которого F значительно меньше средней частоты f_cр. Аналогичный характер функции корреляции был получен в примере 3 [см. (2.45)]. Из (2.50) видно, что сечения высокочастотного квазибелого шума не коррелированы между собой, если интервал между ними τ кратен 1/F, а также если τ = (2n+1)/4f₀, где n - целое число.

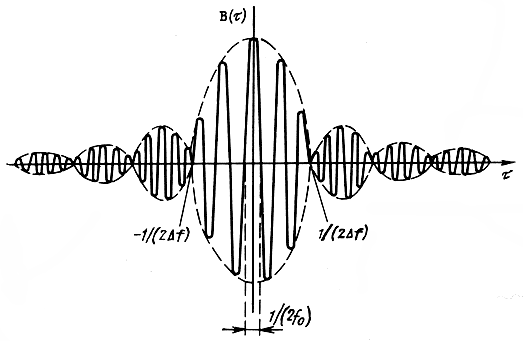
Рис. 2.8. Функция корреляции высокочастотного квазибелого шума

Рассматривая приведенные выше примеры, нетрудно видеть, что увеличение интервала корреляции приводит к сокращению ширины спектра, и наоборот. Это является проявлением общего свойства любой пары функций, связанных между собой преобразованием Фурье.