2.3. Комплексное и квазигармоническое представление сигналов

При изучении гармонических сигналов широко пользуются символическим методом, заменяя действительный сигнал acos(ω₀t + φ) = Re {ae^i(ω₀t+φ)} комплексной функцией Это облегчает решение многих задач и приводит к правильным результатам, если полученное комплексное решение заменить его действительной частью.

Обобщением символического метода является представление любого сложного сигнала x(t) (в частности, реализации случайного процесса) комплексной функцией

где

В частном случае гармонического сигнала a(t) = a = const и θ(t) = ω₀t + φ. При этом сопряженный сигнал x̄(t) = а sin(ω₀ + φ) отличается от действительного сигнала только сдвигом фазы на -π/2. Естественно и в общем случае не гармонического сигнала x(t) определить сопряженный сигнал как результат поворота фаз всех гармонических составляющих с положительными частотами на -π/2, а с отрицательными частотами - на +π/2. Другими словами, если сигнал представлен рядом Фурье

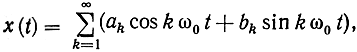
то

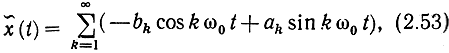
а если интегралом Фурье

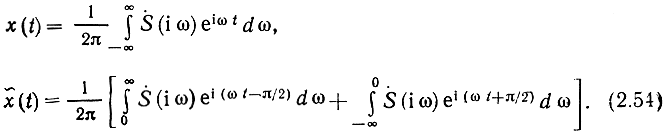
Можно показать, что два сигнала x(t) и x̄(t), удовлетворяющие этим условиям, связаны между собой следующими линейными интегральными преобразованиями, называемыми преобразованиями Гильберта:

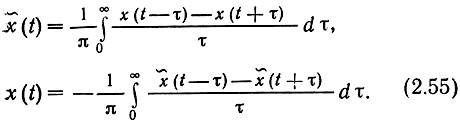
Комплексный сигнал x(t)+ix̃(t), если x̃(t) определено по (2.55), называют аналитическим (или гильбертовским) сигналом. Поскольку фазы всех составляющих спектральной плотности S_x̃(iω) сопряженного сигнала x̄(t) в области положительных частот сдвинуты на -π/2 относительно S_x(iω), а умножение на i означает сдвиг фаз на +π/2, ix̃(t) имеет в области положительных частот такой же спектр, как и x{t). В области же отрицательных частот преобразование Гильберта соответствует повороту фаз на + π/2, и поэтому в спектре ix̃(t) фазы отрицательных частот сдвинуты на я относительно спектра x(t). В результате спектр аналитического сигнала в области отрицательных частот тождественно равен нулю, тогда как в области положительных частот спектры x(t) и ix̃(t) складываются в одной фазе:

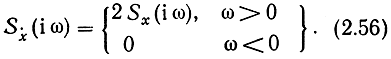
Все сказанное можно распространить и на случайные процессы. Ансамбль комплексных функций действительной переменной t, Ẋ(t) = X(t) + iY(t) с заданными n-мерными распределениями вероятностей представляет собой комплексный случайный процесс, который можно рассматривать как совокупность двух действительных процессов Х(t) и Y(t).

Математическое ожидание комплексного случайного процесса

представляет собой в общем случае комплексную функцию времени. Его дисперсия D(X(t)} = М{|X̊(t)|²} также в общем случае является функцией времени, но не комплексной, а действительной и к тому же неотрицательной. Здесь X̊(t) = Ẋ(t) - M{Ẋ(t)} - центрированный процесс.

Функция корреляции комплексного процесса определяется следующим образом:

где * означает комплексно-сопряженную величину, которая является в общем случае комплексной функцией двух действительных аргументов. При этом В_Ẋ(t₂, t₁) = B*_Ẋ(t₁, t₂). Легко убедиться, что В_Ẋ(t₁, t₁) = D{Ẋ(t₁)}.

Комплексный случайный процесс стационарен (в широком смысле), если его математическое ожидание не зависит от времени, а функция корреляции зависит только от τ = t₂-t₁. Из этого следует, что и дисперсия стационарного комплексного процесса не зависит от времени.

В дальнейшем будем говорить только об аналитических комплексных случайных процессах, в которых Y(t) = X̃(t):

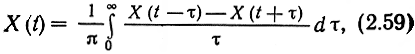
Аналитические случайные процессы обладают свойствами, аналогичными детерминированным аналитическим сигналам. В частности, если действительный случайный сигнал X(t) имеет нормированный (двусторонний) энергетический спектр (НЭС) γ_X(f), то у аналитического сигнала

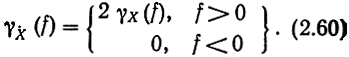
Таким образом, НЭС аналитического сигнала совпадает с односторонним НЭС его действительной части.

Важным параметром аналитического сигнала является функция взаимной корреляции между X(t) и X̃(t):

Для стационарного аналитического сигнала эта функция зависит только от разности t₂ - t₁ = τ, причем при τ = 0 она равна нулю, в чем легко убедиться из (2.59):

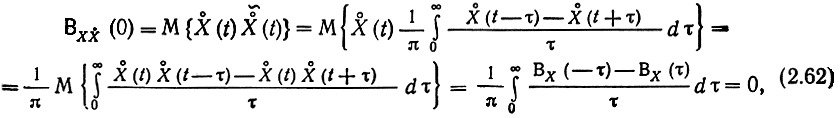
так как для стационарного процесса B_X(-τ) = В_Х(τ). Таким образом, функции X(t) и X̃(t) не коррелированы в совпадающие моменты времени.

Представим аналитический случайный сигнал в экспоненциальной форме:

где

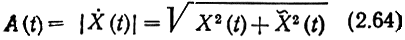
- действительный неотрицательной случайный процесс, называемый огибающей сигнала X(t); Ψ(t) - действительный случай ней процесс такой, что

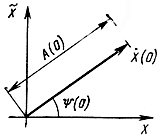
Рис. 2.9. Представление аналитического сигнала вращающимся вектором

Очевидно, что огибающая и фаза полностью определяются (в вероятностном смысле) действительным сигналом X(t). Из определения огибающей видно, что A(t)≥|X(t)|, а в тех точках, где имеет место равенство A(t) = Х(t), сигнал и его огибающая имеют одинаковые производные^*.

^* (Аналогично тех точках, где A(t) = -X(t), имеет место равенство )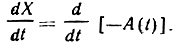

Аналитический случайный сигнал можно представить случайным векторным процессом на комплексной плоскости. На рис. 2.9 показана одна из реализаций вектора Ẋ(t) в момент t = 0. Длина этого вектора A(0), а угол между ним и действительной осью Ψ(0). С течением времени конец вектора перемещается по некоторой траектории, так что в любой момент его длина равна A(t) и он образует угол Ψ(t) с действительной осью.

Угловая скорость Ω(t) = dΨ/dt вектора Ẋ(t) называется мгновенной частотой сигнала. Ее можно выразить через действительный сигнал X(t) и сопряженный с ним сигнал X̃(t):

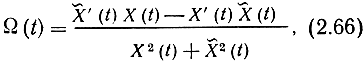
где штрихи обозначают производные по времени. В частности, как легко убедиться, для гармонического сигнала x(t) = a cos(ω₁t + φ) = Re[ae^i(ω₁t+φ)] мгновенная частота совпадает с ω₁.

Выберем некоторую произвольную частоту ω₀ и обозначим Φ(t) = Ψ(t) - ω₀t. Тогда

Случайная функция Φ(t) называется мгновенной начальной фазой относительно частоты ω₀. Очевидно, что она зависит от выбора ω₀.

Действительный сигнал и сопряженный с ним можно представить в квазигармонической форме, непосредственно вытекающей из (2.67):

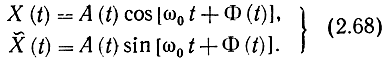
Приведем без доказательства одно свойство аналитического сигнала. Если все гармонические составляющие всех реализаций процесса X(t), выраженного (2.68), сдвинуть по фазе на одинаковый угол θ, то полученный при этом процесс, который обозначим Х_θ (t), можно представить в квазигармонической форме X_θ (t) = A (t) cos [ω₀t + Φ(t) + θ]. Отсюда с помощью простых тригонометрических преобразований с учетом (2.68) получим представление

Аналогично, при повороте на -θ