2.4. Огибающая и фаза случайного процесса

Квазигарманичеокое представление возможно для любого сигнала, однако наиболее полезно оно при изучении относительно узкополосных сигналов, у которых ширина спектра значительно меньше средней частоты f_ср. Для таких сигналов огибающая A(t) является низкочастотным процессом, т. е. изменяется медленно по сравнению с изменениями X(t). Это же верно и для мгновенной начальной фазы Φ(t) и для ее производной dΦ/dt = Ω(t) - ω₀ при условии, что частота ω₀ выбрана вблизи средней круговой частоты спектра 2πf_ср. При наблюдении на осциллографе такой процесс имеет вид колебания, промодулированного по амплитуде и фазе.

Выражение (2.67) можно переписать также следующим образом:

где Ȧ(t) = A(t)e^iΦ(t) - комплексная огибающая сигнала. В отличие от действительной огибающей A(t), комплексная огибающая не определяется однозначно сигналом X(t), а зависит также от выбора произвольной частоты ω₀. Из очевидного равенства

следует, что комплексную огибающую можно рассматривать как результат сдвига спектра аналитического сигнала вниз на ω₀^*.

^* (Отсюда, между прочим, видно, что спектр A(t) не лежит полностью в области f>0, и, следовательно, комплексный процесс A(t) не является аналитическим.)

Введем обозначения для действительной и мнимой частей комплекеной огибающей:

С помощью этих функций можно получить еще 0дно полезное представление сигнала X(t):

Таким образом, сигнал X(t) разложен на две квадратурные составляющие: A_c(t)cos ω₀t и A_s(t) sin ω₀t.

Функции A_c(t) и A_s(t) зависят от выбора частоты ω₀. Для узкополосного сигнала эти функции при надлежащем выборе являются, как и A(t), медленно меняющимися (низкочастотными). Их, однако, не следует называть огибающими квадратурных составляющих, поскольку, в отличие от A(t), они принимают не только положительные, но и отрицательные значения.

Зная функции распределения исходного процесса X(t), можно обычными методами теории вероятностей найти функции распределения для всех вновь введенных процессов: X̃(t), Ẋ(t), A(t), Ψ(t), Φ(t), ω(t) и т. д. В общем случае это не простая задача. Поэтому остановимся подробнее только на наиболее важном случае для практики, когда X(t) - гауссовский процесс.

Рассмотрим вначале центрированный стационарный гауссовский процесс X(t). Поскольку преобразование Гильберта линейно, то, учитывая инвариантность нормального распределения при любых линейных операциях, можно утверждать, что X̃(t) - также гауссовский процесс.

На основании того, что X̃(i) отличается от X(t) только сдвигом фаз всех составляющих, и учитывая, что спектральная плотность мощности G(f) не зависит от фазовых соотношений, приходим к выводу, что G_X̃(t) = G_X(f). Из этого на основании теоремы Хинчина - Винера следует равенство корреляционных функций В_X̃(τ) = В (τ), а отсюда и равенство дисперсий D{X̃(t)} = B_X̃(0) = B_X(0) = D{X(t)}. В совпадающие моменты времени X(t) и X̃(t) между собой не коррелированы [(см. 2.62)], а поскольку они гауссовские, то и независимы. Комплексная огибающая Ȧ(t), полученная из X(t) посредством линейной операции (2.70а), обладает теми же свойствами: A_c(t) и A_s(t) также являются центрированными гауссовскими процессами, независимыми в совпадающие моменты времени. Дисперсия аналитического сигнала

Такова же, как легко проверить, и дисперсия комплексной огибающей Ȧ(t). Нетрудно также убедиться в том, что D{A_C (t)} = D{A_s(t)} = D{X(t)}^*.

^* (Если спектры A_c(t) и A_s(t) лежат в полосе частот от 0 до F, то в соответствии с (2.46) ширина спектра X(t) равна 2F. Поэтому средняя спектральная плотность A_c(t) (или A_s(t)) в указанной полосе вдвое больше средней спектральной плотности X(t).)

Совместную плотность вероятности X(t) и X̃(t) в одном сечении t можно записать на основании (2.12) так:

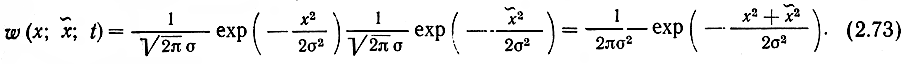
Здесь σ² - дисперсия, одинаковая для X и для X̃.

Процессы A(t) и Ψ(t), полученные из X(t) и X̃(t) с помощью нелинейных операций, стационарны, но, конечно, не являются гауссовскими. Найдем совместную функцию распределения A и Ψ в некотором сечении, т. е. функцию F(a, ψ) =Р{А (t) ≤ a; Ψ(t) ≤ ψ}.

Геометрическая интерпретация этой задачи представлена на рис. 2.10, где по оси ординат отложены значения x̃(t), а по оси абсцисс - значения x(t). Искомая функция распределения является вероятностью того, что конец вектора, представляющего аналитический сигнал Ẋ(t), находится внутри заштрихованной области V.

Для определения функции распределения F(a, Ψ) можно проинтегрировать (2.73) по области V. Переходя при этом к полярной системе координат р, .ф по известным формулам^* x = ρcosφ; х = ρ sin φ; dx dx = ρdρdφ, получим

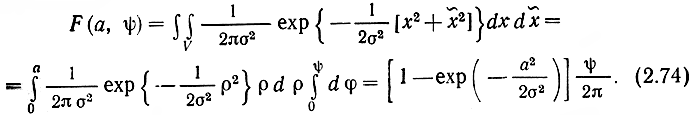
Таким образом, двумерная функция распределения оказалась произведением двух одномерных функций:

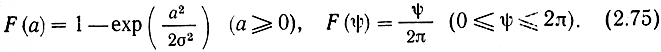
^* (Заметим, что при этом фаза Ψ(t) определяется с точностью до величины, кратной 2π, иначе говоря, по модулю 2π. Это не влияет на изучение процесса X(t), поскольку Ψ(t) фигурирует как аргумент косинуса или синуса.)

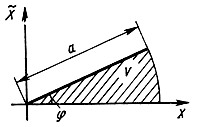
Рис. 2.10. К вычислению распределения вероятностей огибающей и фазы центрированного нормального процесса

Это значит, что огибающая A(t) и фаза Ψ(t) в одном сечении независимы^*.

^* (Можно показать, что в центрированном стационарном гауссовском процессе A(t) и Ψ(t) независимы и в разных сечениях.)

Плотность распределения огибающей найдем как производную функции распределения:

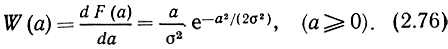
Это известное распределение Рэлея, график которого показан на рис. 2.11 вместе с графиком гауссовского распределения мгновенных значений w(x).

Для плотности вероятности фазы имеем (рис. 2.12)

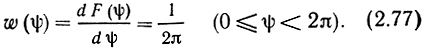
Следовательно, фаза стационарного гауссовского центрированного процесса распределена равномерно на интервале протяженностью 2π.

Мгновенная начальная фаза Φ(t) рассматриваемого процесса также равномерно распределена на интервале протяженностью 2π. Действительно, можно отыскать совместную функцию распределений A(t) и Φ(t), исходя из плотности процессов A_c(t) и A_s(t) (2.71). Повторяя буквально те же рассуждения и выкладки, только с заменой X, X̃ и ψ на A_с, A_s и Φ, найдем, как и следовало ожидать, плотность (2.76) для A(t) и равномерную плотность вероятностей для Φ(t).

Воспользуемся этим методом для рассмотрения несколько более сложного случая - суммы стационарного центрированного гауссовского процесса и гармонического сигнала:

где Ẋ(t)-центрированный стационарный гауссовский процесс; u и ω_с - некоторые постоянные. Этот случай нередко встречается на практике, когда u cos ω_ct представляет регулярный сигнал, a X̊(t)-флуктуационный шум. Заметим, что Х(t) - нестационарный процесс, так- как его математическое ожидание зависит? от времени.

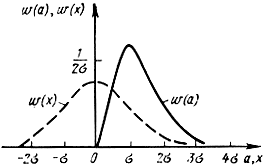
Рис. 2.11. Плотности вероятностей мгновенного значения и огибающей нормального центрированного процесса

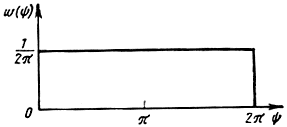
Рис. 2.12. Плотность вероятности фазы нормального центрированного процесса

Представив X(t) в форме (2.72) и выбирая ω₀ = ω_с, можем записать:

где A_s(t) = -A(t) sin Φ(t) = Å_s(t); A_c(t) = A(t) cos Φ(t) = A_c(t) + u;

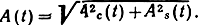
Отсюда видно, что A_c(t) и A_s(t) являются стационарными гауссовскими процессами с одинаковыми дисперсиями σ², взаимно не корелированными в совпадающие моменты времени. При этом M{A_s(t)} = 0, а М{A_с(t)} = u.

Для нахождения функции распределения

рассмотрим совместную плотность распределения вероятностей A_c(t) и A_s(t) в некотором сечении t:

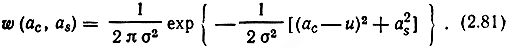
Функция распределения (2.80) равна интегралу от (2.81) по площади, определяемой (2.80). Переходя к полярным координатам a_c = ρ cosξ, a_s = ρ sin ξ на ходам

Не будем вычислять этот интеграл. Заметим лишь, что F(a, φ) в этом случае не выражается произведением двух функций распределения F(a)F(φ), т. е. A(t) и Φ(t) не являются независимыми. В дальнейшем потребуется только распределение вероятностей A(t). Для нахождения F(a) нужно в (2.82) положить φ = 2π, так как по определению 0≤φ<2π и вероятность того, что φ≤2π, равна 1, поэтому F(a, φ) при φ = 2π совпадает с F(a). Итак,

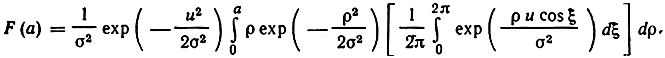
Из теории бесселевых функций известно, что

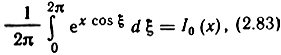
где I₀(х) - модифицированная функция Бесселя нулевого порядка:

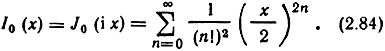
При х = 0 эта функция равна единице и монотонно возрастает с х. Таким образом,

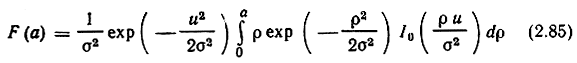
и плотность вероятностей A(t) для суммы гауссовского шума и гармонического сигнала

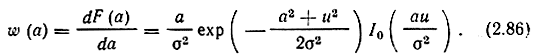
Распределение вероятностей, выраженное (2.86), называется обобщенным распределением Рэлея, или распределением Рэлея-Райса. Очевидно, обычное распределение Рэлея (2.76) является частным случаем распределения (2.86) при u = 0.

Заметим без доказательства, что и в более общем случае суммы гауссовского шума с синусоидальным сигналом

где η - любая детерминированная или случайная начальная фаза, огибающая A(t), подчиняется распределению (2.86). В частности, если η равномерно распределена на интервале протяженностью 2π, то начальная фаза Φ(t) также равномерно распределена на том же интервале и не зависит от A(t). Процесс X(t) в этом случае стационарен.

На рис. 2.13 показаны графики плотности (2.86) при разных значениях u. Легко видеть, что чем больше u/σ, т. е. чем больше отношение амплитуды гармонического сигнала к среднеквадратической величине шума, тем больше и наиболее вероятное значение а/σ.

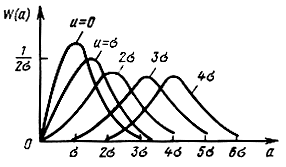
Рис. 2.13. Плотность вероятности огибающей суммы гармонического сигнала и гауссовского шума