
2.5. Пространство сигналов
Подойдем теперь к описанию ансамбля сигналов с иной точки зрения, обращая внимание на соотношения между входящими в ансамбль сигналами. Начнем с самого простого примера. Пусть ансамбль состоит из сигналов, заданных на интервале времени (О, Т) и имеющих вид A sin(ktω0 + (D) , где ω0 = 2π/T, k - постоянное целое число, А - может принимать любые неотрицательные значения, а Φ - любые значения на интервале (0, 2π). Эти сигналы представляют собой синусоиды одной и той же частоты, но с разными амплитудами и начальными фазами, причем на интервале времени длительностью Т укладывается целое число периодов.
Будем изображать каждый из этих сигналов вектором на плоскости с прямоугольными координатами XY, начинающимся в начале координат, имеющим длину l, пропорциональную А и направленным под углом Φ относительно оси X. Очевидно, что каждому сигналу из ансамбля соответствует Y определенный вектор, а каждому вектору - определенный сигнал.
Проекции вектора на оси X и Y равны, соответственно, A cos Φ и A sin Φ.
Легко убедиться, что сумме двух сигналов ансамбля a1 sin(ktω0 + φ1) + а2 sin(ktω0 + φ2) соответствует сумма двух векторов s1 + s2, соответствующих суммируемым сигналам. Для этого достаточно представить эту сумму в виде a1sin φ1×sin ktω0+a1sin φ1cos ktω0+a2cos φ2sin ktω0+a2sin φ2cos ktω0=(a1sin φ1 + a2sin φ2)cos ktω0+(a1cosφ1+a2cos φ2)sin ktω0.
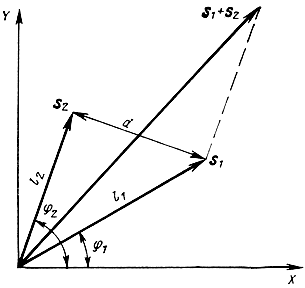
Рис. 2.14. Сумма двух векторов расстояние d между ними
Как видно из рис. 2.14, сумма векторов s1 и s2 имеет проекцию на ось X l1cos φ1 + l2cos φ2, а на ось Y - l1sin φ1 + l2sin φ2 и, следовательно, соответствует сумме сигналов.
Если для длины векторов выбрать масштаб √T/2, то квадрат длины вектора равен энергии сигнала:
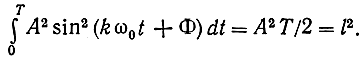
Расстоянием между векторами будем называть расстояние d между их концами. Как известно из тригонометрии, d2 = l21 + l22-2l1l2×cos (φ2-φ1) = l21 + l22-2(s1, s2). Здесь (s1, s2) = l1l2cos(φ2-φ1) - скалярное произведение векторов s1 и s2. Таким образом, с увеличением скалярного произведения векторов расстояние между ними уменьшается. Покажем, что при принятом масштабе скалярное произведение совпадает с интегралом от произведения сигналов:
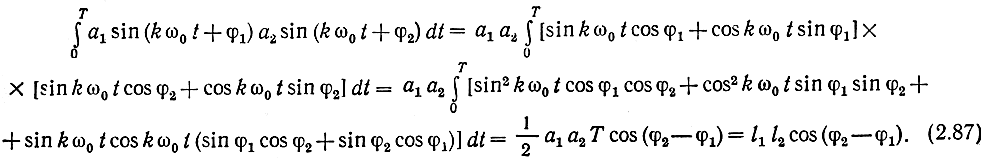
Помеха, добавляющаяся к сигналу, смещает конец соответствующего ему вектора. Поэтому, чем меньше расстояние между двумя векторами, тем вероятнее, что помеха приведет к невозможности уверенно отличить один сигнал от другого, что является причиной ошибочного приема переданного сигнала. Таким образом, векторное представление сигналов помогает изучать вопросы помехоустойчивости системы связи.
Распространим теперь векторное представление на более сложные ансамбли сигналов. Для начала добавим к данному ансамблю сигналы вида Bsin ntω0 (где n≠k - целое число; В принимает любое действительное значение), а также всевозможные суммы вида A sin(ktω0 + Φ) + В sin ntω0. Такой расширенный ансамбль уже нельзя представить векторами на плоскости. Однако его легко изобразить векторами в трехмерном пространстве с проекциями √T/2 A cos Φ на ось Х, √T/2 A sin Φ на ось Y и √T/2 В на ось Z. Легко убедиться, что квадрат длины вектора по-прежнему равен энергии сигнала, и все, что было сказано о расстояниях и скалярных произведениях, остается в силе. В частности, векторы, изображающие сигнал В sin ntω0 и любой из сигналов A sin(ktω0 + Φ), ортогональны, т. е. их скалярное произведение равно нулю, что соответствует известному факту: при n≠k и ω0 = 2π/Т
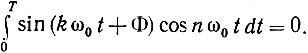
Расширим ансамбль, введя дополнительно сигналы вида В cos ntω0 и всевозможные их суммы, что даст в результате общий вид сигнала A sin(ktω0 + Φ) + В sin(ntω0 + Ψ).
Для того чтобы представить такие сигналы векторами, понадобятся уже проекции на четыре взаимно перпендикулярные оси: √Т/2A cos Φ, √T/2 A sin Φ, √T/2 B cos Ψ и √T/2B sin Ψ. Другими словами, такие сигналы можно представить векторами в четырехмерном пространстве. Хотя физическое пространство, в котором мы живем, трехмерное, в математике уже давно изучены пространства с любым конечным и даже бесконечным числом измерений и получены все их основные свойства. Такие абстрактные пространства изучаются в функциональном анализе и помогают разобраться в поведении различных множеств функций. Это позволяет практически все сигналы, как дискретные, так и непрерывные, представлять в виде векторов. Поэтому для изучения теории передачи сигналов необходимо иметь общее представление об основах функционального анализа, к изложению которых мы и приступаем.
В функциональном анализе множество любых элементов х, y,... называется линейным (или векторным) пространством, если юно удовлетворяет следующим условиям:
1. Для любых двух элементов хну однозначно определен третий элемент х+y, называемый их суммой и также входящий в данное пространство, причем х + y = y + х; x + (y + z) = (х + y) + z.
2. В линейном пространстве существует нулевой элемент, обозначенный 0, такой, что х + 0= х для всех х.
3. Для каждого элемента х линейного пространства существует противоположный ему элемент (-х), такой, что х + (-x)=0.
4. Любой элемент пространства можно умножить на любое число из некоторого множества {α}, называемого множеством скаляров* причем ах также принадлежат данному пространству, и выполняются следующие соотношения: 1х = х, (α + β)x = αx + βx, α(х + y) = αх + αy, α(βх) = (αβ)х.
* (Множество {α} должно быть полем, т. е. на нем должны быть определены операции сложения и умножения с коммутативными и дистрибутивными свойствами и оно должно содержать нуль и единицу. Примерами полей являются множества всех целых чисел, всех действительных чисел, всех комплексных чисел и др. Существуют и конечные поля (см. ниже). )
Примерами линейных пространств могут служить:
множество векторов на плоскости с обычным определением векторного сложения и умножения вектора на число;
множество всех действительных (или всех комплексных) чисел с обычными определениями сложения и умножения;
множество упорядоченных последовательностей из n действительных чисел {а1, a2,...., an}, если определить сумму и умножение на скаляр следующим образом:
(а1, a2,...., an) + (b1, b2,...., bn) = (а1+b1, a2+b2,...., an+bn), α (а1, a2,...., an) = (αа1, αa2,...., αan), (2.88)
и т. д.
Во всех приведенных примерах скалярами могут быть любые действительные числа. При другом выборе поля скаляров можно построить, например, такие линейные пространства:
множество всех целых положительных и отрицательных чисел (включая нуль), если поле скаляров содержит тоже только целые числа;
множество, состоящее всего лишь из двух чисел, 0 и 1, если сложение производится по модулю 2, т. е. по правилу
1 + 0 = 0 + 1 = 1, 1 + 1 = 0 + 0 = 0, (2.89)
а скалярами являются также только 0 и 1;
множество упорядоченных последовательностей из n чисел, принимающих значения 0 и 1, при таких же скалярах, причем сложение и умножение производятся поразрядно, т. е. по (2.88), а каждые два числа складываются по модулю 2, т. е. по (2.89). Заметим, что в последних двух пространствах -х = х.
Очевидно, что множества, приведенные в последних двух примерах, не представляли бы линейного пространства, если бы сложение определялось не по модулю 2, а обычным образом, так как не выполнялось бы условие 1. Точно так же не являлось бы линейным пространством (при обычном определении сложения) множество всех положителыных чисел (не выполняются условия 2 и 3) или множество всех действительных (либо комплексных) чисел, не превосходящих по модулю некоторого числа М (не выполняется условие 1).
Особый интерес представляют функциональные пространства, т. е. линейные пространства, элементами которых являются функции. Примером может служить множество всех непрерывных комплекснозначных функций ẋ(t), заданных на интервале - T/2≤t≤Т/2, если скаляры принадлежат полю комплексных чисел.
Элементы любого линейного пространства называются векторами, их можно рассматривать как обобщение понятия обычных векторов на плоскости или в трехмерном пространстве. Многие свойства обычных векторов переносятся на элементы различных линейных пространств. В частности, ниже будут определены "длина" вектора (которую будем называть нормой), угол между двумя векторами, расстояние между векторами и скалярное произведение двух векторов.
Для теории передачи сигналов важным является то обстоятельство, что практически все сигналы (дискретные и непрерывные) и все аддитивные помехи можно рассматривать как векторы в некотором пространстве. Это позволит получить сравнительно просто и наглядно многие важные результаты.
Определим размерность векторного пространства. Особенностью обычных векторов на плоскости (двумерном пространстве) является то, что любой вектор z можно выразить в виде линейной комбинации любых двух непараллельных между собой векторов х и у: z = α1x + α2y. Для трехмерного пространства это не имеет места, однако любой вектор можно выразить линейной комбинацией трех не лежащих в одной плоскости и не параллельных векторов.
Другими словами, в двумерном пространстве три вектора, а в трехмерном пространстве четыре вектора всегда линейно-зависимы. Распространим это понятие на любое линейное пространство.
Элементы х1, х2,..., xk линейного пространства называются линейно-зависимыми, если существуют скаляры α1, α2,..., αk, не все равные нулю, такие, что
α1x1 + α2х2 + ... + αkxk = 0, (2.90)
Очевидно, что в этом случае любой из этих элементов можно выразить линейной комбинацией остальных элементов. Этого нельзя сделать, если (2.90) выполняется только при α1 = α2 = ... = αk = 0. В последнем случае элементы х1 ,..., xk линейно-независимы.
Линейное пространство, в котором можно найти n линейно-независимых элементов, а любые n + 1 элементов линейно-зависимы, называется n-мерным. Если же можно найти произвольное число линейно-независимых элементов, то пространство называется бесконечномерным.
Базисом в n-мерном пространстве называется любая система из п линейно-независимых векторов.
Во многих линейных пространствах можно ввести понятие скалярного произведения двух элементов х и y, которое обозначается (х, y). Скалярным произведением называется число (в некоторых пространствах комплексное), удовлетворяющее следующим условиям:
а) (х, y) = (y, х)* (где * означает комплексную сопряженность);
б) (х, х)≥0, т. е. скалярное произведение вектора на самого себя всегда является действительным неотрицательным числом;
в) (х, х)=0 только тогда, когда х = 0;
г) (αх, y) = α(х, у);
Д) (х, y1 + y2) = (x, y1) + (x, y2).
Из условий а) и г) следует, что
(х, αy) = α*(х, y). (2.91)
Конечномерное пространство со скалярным произведением называется евклидовым.
Нормой вектора х называется неотрицательное число, обозначаемое ||х|| и равное арифметическому значению √(х, х). Из условия в) следует, что ||х|| = 0 только для нулевого вектора. Из условия г) вытекает важное свойство нормы: ||αх||= |α| × ||х||. В частности, при α = - 1 отсюда следует ||-х|| = ||х||. Для обычных векторов нормой, как легко убедиться, является длина.
Расстоянием между векторами х и y, которое обозначается d(x; y), называют норму разности этих векторов:
d(x, y) = ||х-y||. (2.92)
Очевидно, что d(y, х) = ||y-х|| = ||-(х-y)|| = ||х-y|| = d(x; у).
Важную роль в математике играет неравенство Коши - Буняковского - Шварца, справедливое для всех линейных пространств:
|(х, y)≤||х||×||y||. (2.93)
Для его доказательства рассмотрим квадрат нормы элемента αх + y, который, разумеется, неотрицателен:
||αх + y||2 = (αх + y, αх + y)≥0.
Раскрывая скалярное произведение с помощью (2.91), найдем
(αх + y, αх + y) = |α|2(х, х) + α (х, y) + α* (γ, х) + (y, y) ≥ 0 (2.94)
при всех значениях α. Положим α = -(х, y)*/(х, х) и подставим это значение в (2.94):
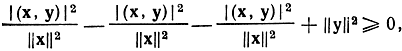
откуда непосредственно следует (2.93). Заметим, что в (2.93) имеет место равенство, если y = βх, где β - любой скаляр.
Из неравенства (2.93) вытекают важные свойства нормы и расстояния:
||х + y|||≤||х|| + ||y||, d(х, z) + d(y, z)≥d(x, y). (2.95)
Доказательство этих неравенств предоставляем читателю. В применении к обычным векторам на плоскости оба эти неравенства характеризуют известный из элементарной геометрии факт - длина стороны треугольника меньше суммы длин двух других сторон. Поэтому их часто называют "соотношением треугольника".
В пространстве обычных векторов на плоскости скалярное произведение определяется, как известно, следующим образом:
(х, y) = ||х||×||y||×cos φ,
где φ - угол между векторами. Нетрудно убедиться, что при этом выполняются условия (2.91).
По аналогии с этим определим угол φ между элементами х и y любого евклидова пространства как
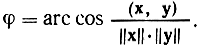
Это определение корректно, так как из неравенства (2.93) следует, что |cos φ| ≤ 1.
В частности, если (х, y) = 0, то φ = ±π/2 и элементы пространства х и у называются ортогональными.
Подмножество векторов {хk} в евклидовом пространстве называется ортогональной системой, если (хk, xl)=0 при k≠l.
Элементы ортогональной системы линейно-независимы. Действительно, если в (2.90) все хi взаимно ортогональны, то, умножая обе части уравнения скалярно на х1 найдем, что α1 = 0. Так как то же самое можно получить для всех αi, то из этого следует линейная независимость ортогональных векторов. В любом n-мерном пространстве можно построить полный ортогональный базис, т. е. систему из n ортогональных векторов.
Ортогональный базис, удовлетворяющий условию
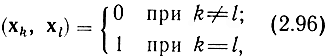
называется ортонормированным. Очевидно, что по любому ортогональному базису {хk} можно построить ортонормированный, заменив все xk на хk/||хk||.
Ортогональный базис в линейном пространстве определяет некоторую систему декартовых координат. Каждый вектор можно представить проекциями на эти координатные оси. Такое представление является разложением вектора по данному ортогональному базису.
Пусть {φk} - полный ортогональный базис, а х - некоторый вектор в данном пространстве. Определим числа ck следующим образом:
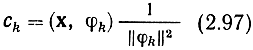
и построим ряд kΣ ckφk В случае конечномерного пространства этот ряд вырождается в конечную сумму. Имеет место равенство
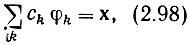
называемое разложением вектора х по базису {φk}. В случае конечномерного пространства это равенство понимается в обычном смысле, в случае же бесконечномерного пространства - в смысле сходимости по норме, т. е.
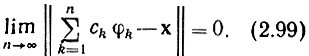
Ряд (2.98) называют обобщенным рядом Фурье, а числа ck - коэффициентами Фурье по данному базису.
Докажем равенство (2.98) для конечномерного пространства. Предположим, что оно неверно. Тогда вектор
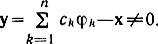
Умножим его скалярно на любой вектор φi из данного ортогонального базиса. Учитывая (2.97), получим
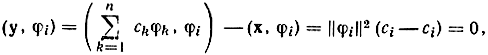
и так как по предположению y - ненулевой вектор, то он ортогонален всем векторам базиса, что противоречит полноте базиса. Это противоречие и доказывает (2.98). Аналогичное доказательство можно провести и для бесконечномерного базиса, но потребуются более тонкие аргументы для доказательства сходимости ряда.
В случае ортонормированного базиса ||φk|| = 1. Тогда, умножив скалярно обе части равенства (2.98) на вектор х, найдем
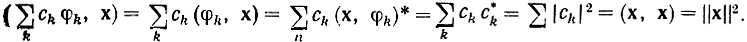
Равенство
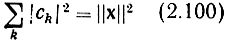
называется равенством Парсеваля. Оно выполняется для любого вектора только при полном ортонормированном базисе.
Два векторных пространства х и у называются изоморфными, если между элементами х и у можно установить взаимно-однозначное соответствие и при этом выполнить следующие условия: если элементам xk и xl соответствуют элементы yk и yl, то элементу xk+xl соответствует yk + yl элементу αxk соответствует αyk и (хk, хl) = (yk, yl). Очевидно, что если пространство A изоморфно B ,а B изоморфно E, то и A изоморфно E.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
