2.6. Особенности некоторых пространств сигналов

Рассмотрим некоторые функциональные пространства, широко используемые в теории связи. Одним из них является евклидово n-мерное пространство R_n. Его образует, например, множество периодических функций X(t) с периодом Т, представляемых в виде конечной тригонометрической суммы (разложения по ортогональному базису):

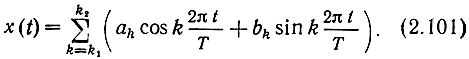
Скалярное произведение в этом пространстве

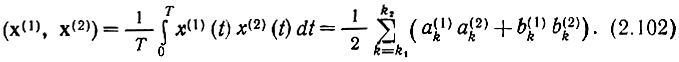
Такое же пространство образуют финитные функции, заданные на интервале (0, Т) или (-T/2, Т/2) и т. д., если на этом интервале их можно представить суммой (2.101).

Эти пространства изоморфны пространству n-мерных векторов, представляющих упорядоченные последовательности из n действительных чисел (l₁, l₂,..., l_n) со скалярным произведением

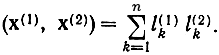
Важную роль в теории играет бесконечномерное пространство L₂(T) финитных функций с интегрируемым квадратом или периодических функций с периодом Т. Их можно представить на интервале (0, Т) рядом Фурье (2.101) при k₂ = ∞. Скалярное произведение определяется также (2.102). Это пространство изоморфно пространству l₂ бесконечных упорядоченных последовательностей чисел х = (l₁ l₂,... ), удовлетворяющих условию

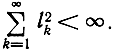
Функции с интегрируемым квадратом, заданные на бесконечной оси времени, образуют пространство L₂(∞), в котором скалярное произведение

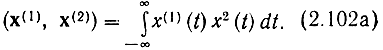
В функциональном анализе доказывается, что действительные пространства l₂, L₂(T) и L₂(∞) изоморфны.

Аналогичные функциональные пространства образуют и комплексно-значные функции при соответствующем определении скалярного произведения. Так, для комплексного пространства L₂(T)

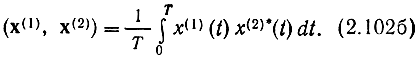
Оно изоморфно пространству l₂ бесконечных последовательностей комплексных чисел х = (l₁, l₂,...), удовлетворяющих условию Σ|l_k|^@<∞ для которого скалярное произведение

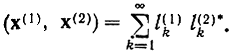
Заметим, что неравенство Коши - Буняковского - Шварца (2.93) в пространстве L₂ принимает вид

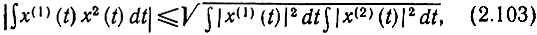
причем пределы интегрирования охватывают область определения пространства, например, от -T/2 до T/2 для пространства L₂(Т) или от -∞ до +∞ для L₂(∞).

В теории передачи сигналов два сигнала, x(t) и y(t), называются ортогональными в усиленном смысле, если соответствующие им аналитические сигналы x(t)+ix̄(t) и y{t)+iȳ(t) также ортогональны. Легко убедиться, что для этого все четыре действительных сигнала x(t), x̄(t), y(t), ȳ(t) должны быть попарно ортогональны.

Рассмотрим еще пространство 2_n, элементами которого являются последовательности n чисел а (а₁, a₂,...., a_k,...., a_n), где аи принимают только значения 0 или 1. Сложение в этом пространстве производится по разрядно по модулю 2:

где знак ⊕ означает сложение по правилу (2.88). В отличие от ранее приведенных примеров это пространство двоичных n-мерных векторов содержит лишь конечное число элементов. Так как каждый член последовательности может принимать только два значения, то всего существует 2ⁿ различных последовательностей длины n.

Скалярное произведение в этом пространстве удобно задать формулой

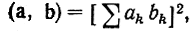
где Σ - сумма в обычном смысле. Отсюда норма двоичного вектора

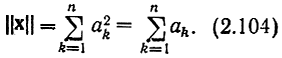
Равенство (2.104) записано на основании того, что 0² = 0, 1² = 1.

Таким образом, нормой двоичного вектора является количество содержащихся в нем единиц. Эту норму называют также весом вектора. Все свойства нормы при этом выполняются; в частности, норма равна нулю только для нулевого вектора, состоящего из одних нулей.

Ортонормированный базис в этом пространстве содержит n векторов:

Других ортонормированных базисов здесь нет, так как все остальные векторы (кроме нулевого) имеют норму не менее 2.

Расстояние между двумя векторами d(а, b) по определению равно норме их разности:

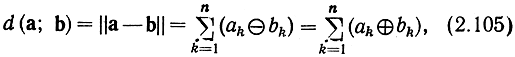
где ⊕ и (-) означают сложение и вычитание по модулю 2, а последнее равенство написано на основании того, что сложение и вычитание по модулю 2 совпадают. Значение a_k⊕b_k равно 1 в том случае, когда a_k≠b_k, если же a_k=b_k то a_k⊕b_k=0. Таким образом, расстояние между двоичными векторами равно числу составляющих, в которых они различаются. Такое определение расстояния было введено Р. Хэммингом и называется расстоянием Хэмминга. Об этом пространстве речь пойдет в гл. 5.

Множество реализаций случайного процесса нередко образует линейное пространство. При этом скалярные произведения, нормы, расстояния оказываются случайными величинами. Заметим, что ортогональный базис состоит из детерминированных функций. В частности, в (2.98) при разложении случайного процесса по ортогональному базису коэффициенты c_k - случайные величины, φ_k - не случайные функции.

Случайные коэффициенты c_k в (2.98), вообще говоря, коррелированы между собой. Для решения многих вопросов полезно иметь разложение процесса по такому ортогональному базису, в котором коэффициенты c_k между собой не коррелированы. Разложение, удовлетворяющее этому условию, называют каноническим. Доказано, что для стационарных случайных процессов всегда существует хотя бы один базис (разный для различных процессов и определяемый корреляционной функцией процесса), при котором разложение оказывается каноническим.

Разумеется, для случайных процессов разложение (2.98) по ортогональному базису понимается в смысле среднеквадратической сходимости [(см. 2.8)].

Важную роль в теории связи играет центрированный случайный процесс с гауссовским распределением, представляемый в пространстве L₂ или R_n вектором, у которого все составляющие имеют гауссовское распределение и взаимно-некоррелированы. Такой процесс является математическим представлением флуктуационного белого или квазибелого шума. Из двух реализаций такого случайного вектора, как легко убедиться, более вероятна та, у которой меньше норма. Это следует из того, что одномерная гауссовская плотность вероятности имеет максимум при нулевом значении аргумента, и из независимости компонент вектора.