2.7. Теорема котельникова

В 1933 г. советский ученый В. А. Котельников доказал весьма важную теорему о функциях с финитным спектром.

Функцию x(t) с финитным спектром можно точно восстановить (интерполировать) по ее отсчетам x(kΔt), взятым через интервалы Δt = 1/(2F), где F - верхняя частота спектра функции. Эго осуществляется с помощью ряда

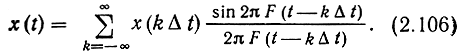
В соответствии с этой теоремой, функцию x(t), заданную на непрерывной оси времени, можно представить с помощью последовательности x(kΔt), заданной на дискретных точках kΔt.

Функции

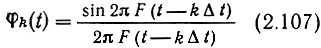
образуют ортогональный (ненормированный) базис в пространстве сигналов с финитным энергетическим спектром, т. е. таких, для которых

Как отмечалось (см. гл. 1, стр. 10), в любой системе связи подавляющая часть мощности сигнала лежит в пределах некоторой ограниченной полосы частот, а в ряде случаев эта полоса искусственно ограничивается. Поэтому случайный процесс с финитным энергетическим спектром является удобной математической моделью для многих реальных сигналов.

Функции φ_k(t) называют функциями отсчета. Три из них изображены на рис. 2.15. Они отличаются друг от друга только сдвигами по времени на интервалы, кратные Δt. Заметим, что при t = nΔt, где n - любое целое число, все функции отсчета, кроме φ_n, равны нулю, а φ_n = 1.

Теорема Котельникова легко доказывается для детерминированных сигналов x(t), имеющих спектр Фурье, удовлетворяющий условию

Идея доказательства заключается в том, что спектральная плотность S(i2πf), отличная от нуля только на конечном интервале (-F, F), может быть разложена на этом интервале в комплексный ряд Фурье. При этом оказывается, что коэффициенты этого ряда с точностью до постоянного множителя 1/(2F) совпадают с отсчетами х(-kΔt) функции x(t). Затем, используя обратное преобразование Фурье, можно показать, что функция x(t) выражается рядом (2.107).

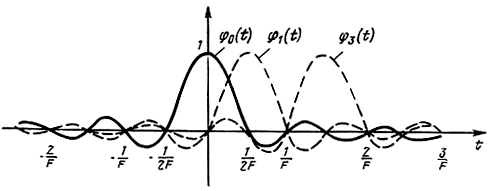
Рис. 2.15. Функция отсчета

Действительно, при разложении S(i2πf) в комплексный ряд Фурье на интервале длиной 2F

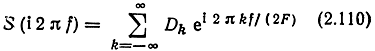
коэффициенты D_k, как известно, выражаются формулой

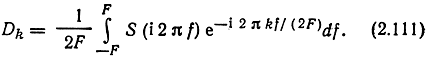
С другой стороны, выражая x(t) обратным преобразованием Фурье, имеем F

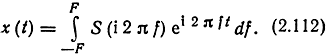
Здесь вместо бесконечных пределов интегрирования взяты пределы -F, F на основании (2.109).

Если в (2.112) подставить значение t = -kΔt = k/(2F), то, сравнивая результат правой частью (2.111), получим

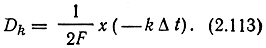
Таким образом,

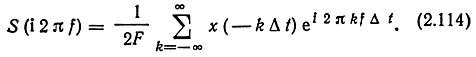
Очевидно, поскольку суммирование производится по всем k, как положительным, так и отрицательным, изменение знака в (2.114) значения суммы не изменит. Таким образом,

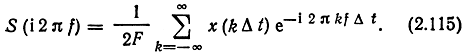
Подставив это выражение в формулу обратного преобразования Фурье 1(2.112), найдем

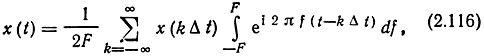
и после интегрирования

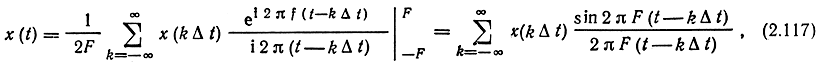
что совпадает с (2.106). Здесь применена известная формула (е^iφ-e^-iφ)/2i = sin φ.

Теорема Котельникова свидетельствует о том, что функции о финитным спектром можно разложить в ряд по ортогональному базису (2.107) в соответствии с общим выражением (2.98). Эту теорему можно обобщить и на случайные процессы. Очевидно, что разложение в ряд (2.106) справедливо для таких случайных процессов, у которых все реализации имеют преобразование Фурье, удовлетворяющее условию (2.109). Однако, как уже отмечалось, такие процессы нестационарны, тогда как для теории связи важно сформулировать и доказать соответствующую теорему для любых случайных процессов, у которых энергетический спектр удовлетворяет условию (2.108). Строгая формулировка теоремы Котельникова в этом случае такова:

для случайного процесса X(t) с энергетическим спектром g_X(f), удовлетворяющим условию (2.108), ряд

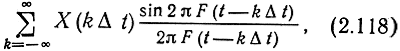
где X(kΔt) - случайные отсчеты (сечения) процесса X(t), взятые через интервалы Δt = 1/(2F)) сходится в среднеквадратическош смысле к процессу X(t).

Доказательство теоремы в такой формулировке можно найти в [13]. Основное значение этой теоремы заключается в том, что она позволяет во многих случаях заменить изучение случайного процесса X(t), заданного на непрерывной оси времени, изучением случайной последовательности X_k = X(kΔt).

По поводу содержания теоремы Котельникова и ее использования необходимо сделать ряд дополнительных замечаний:

1. Равенства (2.108) и (2.109) остаются справедливыми, если вместо верхней частоты спектра F взять любую частоту F'>F* Следовательно, ряд Котельникова можно записать и для Δt = 1/2F'<1/2F. В этом случае удобнее ряд (2.106) записать в такой форме:

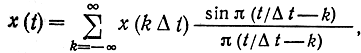
где Δt≤1/2F. Это же относится и к ряду (2.118).

2. Представление непрерывного сигнала x(t) с помощью дискретных отсчетов x(kΔt) называется дискретизацией. На практике каждый отсчет представляется импульсом величиной x(kΔt) и длительностью τ<<Δt. Математической моделью последовательности таких импульсов является сумма дельта-функций:

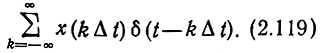
Чтобы преобразовать этот поток импульсов в исходную непрерывную функцию x(t), его нужно пропустить через идеальный фильтр нижних частот с граничной частотой F. Как известно, импульсная реакция такого фильтра

т. е. совпадает с функцией отсчета при k = 0.

Если подставить (2.119) в качестве входного сигнала и (2.120) в качестве импульсной реакции в интеграл Дюамеля [2] и воспользоваться при интегрировании фильтрующим свойством дельтафункции, то сигнал на выходе фильтра

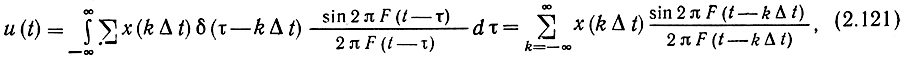
Что совпадает с рядом (2.106), выражающим исходную функцию x(t).

3. В. А. Котельников доказал также аналогичную теорему для полосовых сигналов, т. е. таких, односторонний спектр которых заключен между частотами F₁ и F₂, т. е.

В соответствии с этой теоремой такая функция может быть однозначно восстановлена по ее отсчетам x(kΔt), взятым через интервалы времени Δt = 1/[2(F₂-F₁)]. Если эти отсчеты представить в виде потока импульсов (2.119), то исходную функцию можно, в принципе, точно восстановить, пропустив этот поток через идеальный полосовой фильтр.

4. На практике часто приходится встречаться с сигналами, энергия (или мощность) которых почти полностью сосредоточена на интервале времени от Т₁ до Т₂ и в полосе частот от -F до F. Из теории преобразований Фурье известно, что финитный (во времени) сигнал не может иметь финитный спектр. Однако выделенное выше слово "почти" оправдывает рассмотрение таких сигналов и позволяет представлять их не бесконечным рядом Котельникова, а конечной суммой. Однако такое представление является приближенным.

Будем полагать, что вся энергия сигнала x(t) содержится в полосе частот а все отсчеты за пределами интервала (₁, Т₂) равны нулю. Тогда можно точно записать

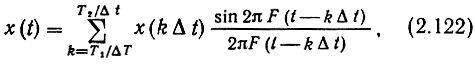
(для простоты считаем Т₁ и Т₂ кратными Δt). Заметим, что конечная сумма в правой части не равна нулю за пределами интервала времени (T₁, T₂), так как каждая функция отсчета φ_k(t) не финитна, а лишь довольно быстро убывает при удалении в любую сторону от своего максимума при t = kΔt.

В случае, когда x(t)-финитный сигнал, в точности равный нулю за пределами интервала (T₁, T₂), спектр его не финитный, но если подавляющая часть его мощности сосредоточена в полосе частот (-F, F), то формула (2.122) является приближенной. Можно показать, что погрешность ее ε(t) определяется той долей энергии сигнала Л?, которая лежит за пределами полосы частот (-F, F), а именно, ε²/х² = ΔЕ.

Достоинство формулы (2.122) заключается в том, что она позволяет представить сигналы с энергией, почти полностью сосредоточенной на интервале времени длиной Т = Т₂-Т₁ и в полосе частот |f|<F, конечным числом отсчетов, а не бесконечным (счетным) числом, как в (2.106). Таким образом, сигналы почти финитные и почти с финитным спектром можно считать элементами конечномерного (евклидова) пространства не бесконечномерного.

Размерность этого пространства определяется числом членов в сумме (2.121), которое равно, как легко убедиться, 2FТ + 1 ≈ 2FТ. Здесь приближенное равенство имеет место, поскольку для рассматриваемых здесь сигналов FT >> 1. Эту величину

называют базой сигнала. Она играет большую роль в теории и технике передачи дискретных сообщений.

Более подробные сведения о случайных процессах можно найти в [4, 11, 14].

Вопросы к главе 2

1. Можно ли считать заданной случайную последовательность A(t_k), если для любого k известны вероятности P(a^(k)_i) для всех а_i?
2. Случайная последовательность а⁽¹⁾, а⁽²⁾, ..., аⁿ представляет собой цепь Маркова. Зависит ли а⁽⁷⁾ от а⁽⁸⁾? Зависит ли а⁽⁷⁾ от а⁽⁴⁾?
3. Какие из четырех реализаций случайного процесса, изображенных на рис. 2.1, удовлетворяют условию X(t₁)≤x₁, X(t₂)≤x₂, X(t₃)≤x₃. То же для условия X(t₂)≤x₁, X(t₃)≤x₁?
4. Всякий детерминированный процесс (т. е. функцию времени) можно рассматривать как частный (вырожденный) случай случайного процесса, имеющего одну единственную реализацию с вероятностью 1. Чему равна функция корреляции такого процесса? Может ли такой процесс быть стационарным?
5. * Могут ли нижеследующие функции τ быть функциями корреляции стационарного процесса? Если нет, то почему? a) sin ατe^|-βτ|; б) cos ατe^|-βτ|;; в) sin ατe^|-βτ|;; г) sin ατ/ατ ; д) 1 - α|τ|: при |τ|>1/α; 0 при |τ|>1/α; е) 1 - α|τ| при |τ|≤1/2α; 0 при |τ|>1/2α; ж) е^-α2.
6. X(t) и Y(t)-два независимых стационарных процесса с ФК В_Х(х) и B_Y(τ). Чему равны ФК процессов Z(t) =X(t) + Y(t), U(t) = X(t) - Y(t) и V(t) = X(t)Y(t)?
7. В условиях предыдущего вопроса -выразите спектральные плотности мощности процессов Z(t), U (t) и V(t) через спектральные плотности G_x(f) и G_Y(f) процессов X(t) и Y(t).
8. Покажите, что для плотности распределения Рэлея (2.76) математическое ожидание Ā (t̄) = σ√π/2, дисперсия D{A(t)} = σ²(2-π/2) и мода (значение а, при котором w(a) имеет максимум) равна σ.
9. * Пусть A(t)-стационарный центрированный процесс. Тогда X(t) = -A (t) cos ωt - нестационарный процесс, а получаемый из X(t) аналитический сигнал X(t) - А (t)е^iωt - стационарный (докажите это). Является ли это недостатком комплексного представления сигналов?
10. Проделайте подробно выкладки для вывода формулы (2.87).
11. Какова размерность пространства сигналов вида X(t) = A₁ cos(k₁tω₀ + φ₁) + A₂ cos(k₂tω₀ + φ₂) + А₃ cos(k₃tω₀ + φ₃) при 0≤t≤T где A₁, А₂, А₃, φ₁, φ₂, φ₃ - случайные величины, k₁, k₂, k₃- различные целые числа, ω₀ = 2π/T?
12. Является ли множество всех четных (положительных и отрицательных) чисел линейным пространством при обычном определении сложения и целых скалярах? А множество всех нечетных чисел? А множество всех чисел, кратных 3?
13. Докажите соотношения треугольника (2.95).
14. Докажите, что функции φ_k(0 (2.107) попарно ортогональны, т. е.
    
    
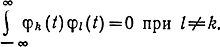
15. Чему равен интервал Δt в ряде Котельникова для сообщения телеметрической системы, в котором максимальная частота F = 10 Гц? То же для телевизионного сообщения с F = 6 МГц.
16. Чему равна база сигнала, соответствующего одному телевизионному кадру, который длится 1/25 с, если ширина его спектра 6 МГц?