3.2. Прохождение сигналов через каналы с детерминированными характеристиками

Передача сигналов по реальным каналам связи всегда сопровождается изменениями (преобразованиями) этих сигналов, в результате чего принятые сигналы отличаются от переданных. Отличия эти обусловлены, прежде всего, линейными и нелинейными преобразованиями входных сигналов, а также наличием аддитивных шумов в канале, существующих чаще всего независимо от передаваемых сигналов. С точки зрения передачи информации по каналу, важно подразделение преобразований сигнала на обратимые и необратимые. Как будет показано (см. § 4.2), обратимые преобразования не влекут за собой потери информации. При необратимых преобразованиях потери информации неизбежны. Для обратимых преобразований сигнала часто используют термин "искажение", а необратимые преобразования называют помехами (аддитивными и не аддитивными).

Примером простейшего детерминированного обратимого преобразования входного сигнала X(t), которое не меняет его форму, служит

В данном случае выходной сигнал канала Y(t) отличается от входного лишь известным масштабом k, который легко компенсируется соответствующим усилением или ослаблением сигнала и постоянной задержкой во времени τ. Она чаще всего невелика. По существу, лишь при связи в масштабах космоса или при очень большом числе реактивных элементов линии связи задержка может оказаться ощутимой^*.

^* (Здесь идет речь о задержке в самой линии связи, а не о задержках в демодуляторе и декодере, которые могут быть значительными и иногда лимитируют возможность повышения помехоустойчивости.)

Если входной сигнал X (t) в (3.1) узкополосный, его удобно представить в квазигармонической форме (2.68): X(t) = A(t)cos× X [ω₀t+Φ(t)], где A(t) и Φ(t) -медленно меняющиеся функции. Поэтому при достаточно малой задержке т можно в первом приближении считать A (t-τ) ≈ A(t) и Φ(t-τ)≈Φ(t), а выходной сигнал в (3.1) записать следующим образом:

где θ_К=ω₀τ - фазовый сдвиг в канале. Таким образом, при узкополосном сигнале малая задержка сводится к некоторому сдвигу фазы.

В реальных каналах связи, даже когда можно пренебречь аддитивным шумом, преобразования сигналов имеют сложный характер и обычно приводят к отличию формы выходного сигнала от входного.

Исследование преобразований случайных процессов при их прохождении через динамические системы (как с регулярными, так и со случайно меняющимися параметрами) связано с решением задач двух типов:

определение корреляционной функции (энергетического спектра) отклика Y(t) на выходе динамической системы, заданной своими характеристиками по данной корреляционной функции (или энергетического спектра) входного воздействия X(t);

определение многомерного распределения отклика Y(t) на выходе заданной динамической системы по многомерному распределению входного воздействия X (t).

Вторая из указанных задач является более общей. Из ее решения, очевидно, может быть получено решение и первой задачи. Однако в дальнейшем в основном ограничимся кратким рассмотрением первой задачи и лишь укажем возможные пути решения второй, более сложной задачи.

Прохождение случайных сигналов через детерминированные линейные цепи. Как известно, линейная цепь с постоянными параметрами характеризуется своей импульсной реакцией g(t) или ее преобразованием Фурье-передаточной функцией k(iω). Если, например, на вход цепи поступает центрированный процесс X(t), то процесс Y (t) на выходе определяется интегралом Дюамеля^*

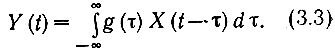
В физически реализуемой цепи при t<0 g(t) = 0. Поэтому нижний предел в (3.3) можно заменить нулем.

^* (Здесь и в дальнейшем интегрирование случайных процессов понимается в среднеквадратическом смысле [см. ф-лу (2.8)].)

Найдем функцию корреляции центрированного выходного процесса Y (t):

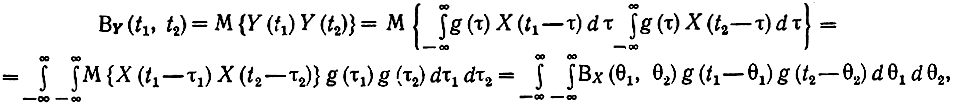
где θ₁ = t₁-τ₁ θ₂ = t₂-τ₂; B_X (θ₁-θ₂) - функция корреляции входного сигнала.

Пусть входной процесс стационарен. Тогда B_X (θ₁-θ₂) = B(θ), где θ=θ₂-θ₁. Введем также обозначения t₂-t₁=τ, t₁-θ₁ = τ₁. Тогда t₂-θ₂ = τ+τ₁-θ и

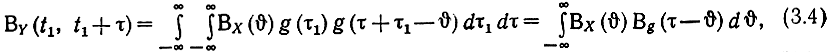
где использована "временная функция корреляции" (ВФК) от неслучайной импульсной реакции

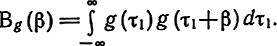
В данном случае β = τ - θ.

Из (3.4) видно, что при стационарном входном процессе и выходной процесс оказывается стационарным, так как B_Y(t₁,t+τ) не зависит от t₁. Поэтому можно записать

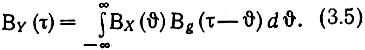
Полученное равенство является аналогом интеграла Дюамеля для корреляционных функций. Таким образом, ФК выходного процесса является интегральной сверткой ФК входного процесса и ВФК импульсной реакции цепи.

Заметим, что ВФК импульсной реакции связана преобразованием Фурье с квадратом модуля передаточной функции |k(iω)|² или амплитудно-частотной характеристики (АЧХ) цепи. Действительно,

ОО ОО

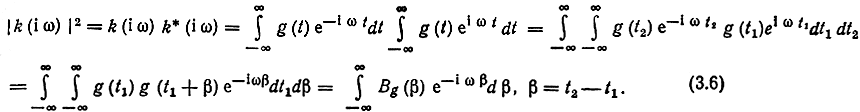
Из теории преобразования Фурье известно, что преобразование Фурье от свертки двух функций равно произведению преобразований Фурье от этих функций. Применив это к (3.5), получим простое соотношение между спектральными плотностями стационарных процессов на входе и на выходе линейной цепи с постоянной передаточной функцией k (iω):

Из (3.5) и (3.7) следует, что ФК и спектр процесса на выходе цепи полностью определяются ФК или спектром процесса на входе и АЧХ цепи, т. е. не зависят ни от распределения вероятностей входного процесса, ни от фазо-частотной характеристики цепи.

Рассмотрим пример прохождения случайных процессов через детерминированные линейные системы - прохождение белого шума с энергетическим спектром N₀ через последовательный колебательный контур с параметрами R, L, С. Если выходное напряжение снимается с емкости, то комплексный коэффициент передачи контура

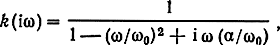
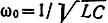
- резонансная частота,

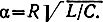
В области малых расстроек |k(ω)|² = ω²₀/{4[β² + (ω-ω₀)²]}, β = R/(2L), и согласно (3.7) энергетический спектр на выходе

Корреляционная функция на выходе

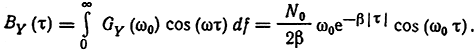
При подаче сигнала X(t) на детерминированную линейную цепь с переменными параметрами выходной сигнал Y(t). как известно, можно выразить интегралом свертки:

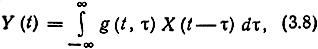
где g(t, τ) - функция двух переменных, определяющая реакцию системы в момент t на δ-импульс, поданный на вход в момент t-τ.

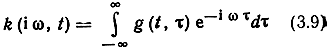
представляет передаточную функцию линейной цепи с переменными параметрами, которая, естественно, является функцией не только частоты, но и времени.

Поскольку в физически реализуемой цепи отклик не может возникнуть раньше воздействия, то g(t, τ)=0 при τ<0. Поэтому в (3.8) и (3.9) нижний предел можно заменить нулем.

Задача нахождения распределения вероятностей отклика линейной системы при произвольном случайном воздействии оказывается в общем случае весьма сложной, даже если ограничиться нахождением одномерного распределения. Отметим, однако, что если на вход линейной детерминированной системы подан гауссовский процесс, то и процесс на выходе оказывается гауссовским, что следует из известных свойств нормального распределения, которое остается нормальным при любых линейных преобразованиях. Если процесс на входе не гауссовский, то при прохождении линейной системы его распределение вероятностей меняется иногда весьма существенно.

Отметим общее свойство, присущее линейным системам. Если полоса частот F_С, занимаемая входным сигналом X(t), много шире полосы пропускания данной линейной системы, то распределение выходного процесса имеет тенденцию приближаться к нормальному. Это можно грубо пояснить, исходя из (3.8). Узкая полоса пропускания означает, что длительность импульсной реакции g(t, τ) как функции τ велика по сравнению с интервалом корреляции входного процесса X(t). Поэтому сечение выходного процесса Y(t) в любой момент t определяется интегралом (3.8), в подынтегральную функцию которого с достаточно большим весом входит много некоррелированных между собой сечений процесса X(t). Распределение вероятностей такого интеграла согласно центральной предельной теореме должно быть близким к нормальному, тем ближе, чем больше отношение ширины спектра входного сигнала к полосе пропускания цепи. В предельном случае, если на вход цепи воздействует белый шум, у которого ширина спектра бесконечна, а цепь имеет ограниченную полосу пропускания, то выходной процесс будет строго гауссовским.

Прохождение узкополосных случайных сигналов через линейные полосовые цепи. Как отмечалось в § 2.4, относительно узкополосные процессы (т. е. такие, у которых ширина спектра значительно уже средней частоты) удобно представлять в квазигармонической форме (2.68). Если средняя частота ω₀ задана, то такой узкополосный сигнал полностью определяется своей комплексной огибающей A(t) (2.70) или ее действительной и мнимой частями (квадратурными составляющими) A_C(t) и A_S(t), которые являются низкочастотными процессами, т. е. их спектры занимают область частот более низких, чем спектр самого сигнала. Такое представление во многих случаях, на этапах синтеза и анализа систем передачи сигналов (сообщений), очень полезно. Так, для представления (2.72) на интервале Т рядом Котельникова потребуется 2T(f₀ + F) отсчетов, для представления же на том же интервале Т двух независимых низкочастотных вещественных функций A_C(t) и A_S(t) (или одной комплексной функции A(t)), достаточно 4FT отсчетов, т. е. примерно в f₀/2F раз меньше.

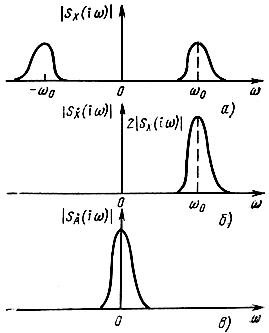
Рис. 3.1. Амплитудные спектры: а - узкополосного сигнала X(t); б - аналитического сигнала Ẋ(t); в - комплексной огибающей A(t)

Заметим также, что при необходимости моделировать узкополосные сигналы и систему связи с такими сигналами на вычислительной машине или при необходимости реализации различных преобразований таких сигналов на основе современной микроэлектронной базы, возникают трудности, чаще всего практически непреодолимые, из-за ограниченного быстродействия этих машин или соответствующих микросхем. Естественно, что значительно проще в этих случаях оперировать низкочастотными эквивалентами сигналов, которыми являются составляющие огибающей.

Выражение для низкочастотного эквивалента Ȧ_x(t) узкополосного сигнала (2.72), определяемое из (2.70,а):

имеет согласно (2.32) спектр по Фурье

Рисунок 3.1 иллюстрирует спектральные соотношения для вещественного узкополосного сигнала X^*(t) (рис. 3.1,а), аналитического сигнала X (t) (рис. 3.1,6) и его низкочастотного эквивалента А̇_Х (t) (рис. 3.1,в).

^* (Полезно напомнить, что спектр S_X(iω) вещественного сигнала X(t) симметричен относительно начала координат, S^*_X(-iω) = S_X (iω) (т. e. амплитудный спектр - четная функция частоты, а фазовый - нечетная, или вещественная часть S_X(iω) - четная функция частоты, а мнимая - нечетная).)

Основная часть реальных непрерывных каналов связи относится к линейным и узкополосным, поэтому сигналы на их выходе могут рассматриваться как реакция на узкополосный сигнал Х(t) полосового фильтра с передаточной функцией k(iωt), модуль которой имеет характер рис. 3.1,а. Преимущества представления сигналов с помощью низкочастотного эквивалента (комплексной огибающей) возникают вследствие того, что полосовую фильтрацию узкополосного сигнала можно интерпретировать как фильтрацую комплексных низкочастотных сигналов комплексными же низкочастотными фильтрами.

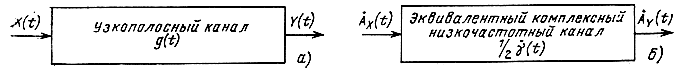
Рис. 3.2. Фильтрация узкополосного сигнала X(t) фильтром с импульсной реакцией g(t) и его низкочастотного комплексного эквивалента A(t) фильтром с импульсной реакцией 1/2γ̇ (t)

Рассмотрим прохождение узкополосного сигнала X(t) через узкополосный канал (полосовой фильтр) с постоянными параметрами и передаточной функцией k(iω) (рис. 3.2,а).

Узкополосный входной сигнал (2.72)

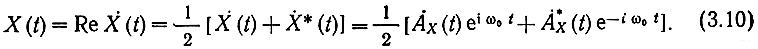
Учитывая предшествующую сноску, нетрудно показать, что спектр сопряженной комплексной огибающей A^*_X(t) = A_C(t) - iA_S(t) равен S^*_ȦX(-iω), где (iω) - спектр по Фурье от A_X(t). Поскольку умножению функции времени на е^±itω₀ соответствует сдвиг спектра по оси частот на ±ω₀, то для спектра Фурье функции X(t), определяемой (3.10), можно записать

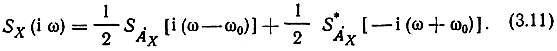
Аналогично полагая, что средняя частота входного сигнала ω₀ совпадает с центральной частотой пропускания фильтра, можно представить передаточную функцию полосового фильтра (преобразование Фурье импульсной реакции фильтра g(t)^*

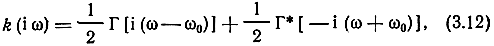
где Γ[i(ω-ω₀)] -спектр Фурье комплексного (аналитического) сигнала ġ(t) = g(t) +ig̃(t) = γ̇(t)e^itω₀ образованного из g(t). Величина Γ(iω) является спектральной характеристикой комплексной огибающей γ̇(t) импульсной реакции фильтра g(t), т. е. низкочастотным эквивалентом узкополосного канала.

^*(Отметим, что функции Γ [i(ω-ω₀)] и Γ*[-i(ω+ω₀)], будучи по модулю симметричными относительно оси ординат для полосового фильтра не перекрываются, так как первая практически целиком лежит в области положительных частот, а вторая отрицательных. Аналогичное утверждение справедливо и для функций S_Ā[i(ω-ω₀)] и S*_Ȧ[-i(ω+ω₀)] узкополосного сигнала.)

Теперь найдем спектр Фурье сигнала на выходе канала y(t). С одной стороны, поскольку этот сигнал узкополосный со средней частотой спектра ω₀, можно аналогично (3.11) записать

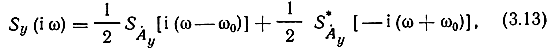
где S_Ȧy[i (ω-ω₀) ] - спектр Фурье комплексного (аналитического) сигнала ẏ(t) = y(t) + iȳ(t) = Ȧ_ye^itω₀, при этом S_Ȧy(iω) является спектром комплексной огибающей Ay(t) выходного сигнала. С другой стороны, для линейной системы с постоянными параметрами спектральные характеристики сигналов на входе и выходе связаны соотношением

Подставляя в (3.14) соотношения (3.11) и (3.12) и учитывая сноску на стр. 78, получаем

(3.15)

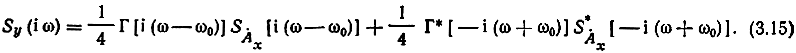
Из (3.13) и (3.15)

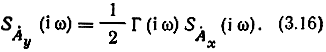
Как следствие комплексная огибающая сигнала на выходе узкополосного канала A_y(t) получается как свертка комплексной огибающей входного сигнала A_x(t) и комплексной огибающей импульсной реакции фильтра γ̇(t)

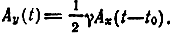
Если фильтр неискажающий, т. е. Γ(iω) = γe^-it₀ω или ġ(t) = γδ(t-t₀), то, используя фильтрующее свойство б-функции, из (3.17) получим

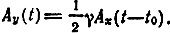
Запишем комплексные огибающие через синфазные и квадратурные компоненты:

Тогда из (3.17)

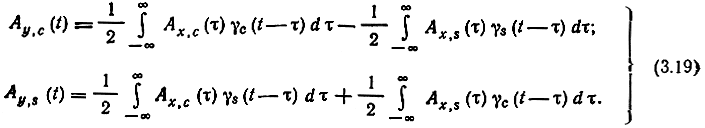
В частной области соотношения (3.19) принимает вид:

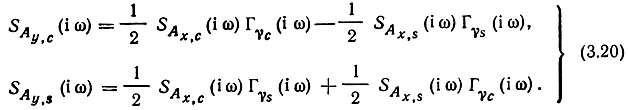
Итак, полосовая фильтрация с передаточной функцией k (iω) узкополосного

процесса x(t) эквивалентна низкочастотной фильтрации с передаточной функцией Γ(iω) комплексного низкочастотного процесса Ȧ_x(t) (см. рис. 3.2).

Процессы А_Х,С и А_Х,S можно получить из x(t) в устройстве, функциональная схема которого представлена на рис. 3.3,а. Действительно, умножая x(t) на 2cos ω₀t получим

а ФНЧ пропустит только первый низкочастотный остальные два члена являются высокочастотными и будут фильтром задержаны. Аналогично во второй ветви выделится квадратурная составляющая A_X,S(t).

Теперь рассмотрим, как можно реализовать комплексную низкочастотную фильтрацию (3.19) или (3.20) три помощи реальных низкочастотных фильтров (у такого фильтра отклик на вещественный сигнал вещественен или передаточная функция удовлетворяет условию сноски на стр. 77), оперируя квадратурными составляющими. Это осуществляется согласно (3.19) или (3.20) двухканальной фильтрацией вещественных низкочастотных синфазной и квадратурной компонент (рис. 3.3,6).

Прохождение случайных сигналов через нелинейные цепи. Ограничимся рассмотрением только безынерционных нелинейных систем с регулярными параметрами, у которых вход и выход связаны некоторой нелинейной зависимостью, называемой характеристикой системы:

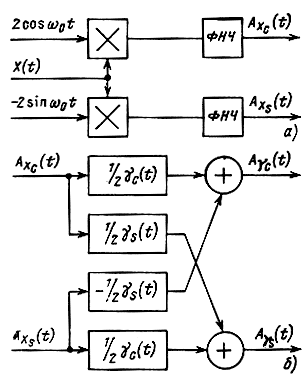
Рис. 3.3. Фильтрация узкополосного сигнала X(t) посредством эквивалентной низкочастотной фильтрации: а - формирование квадратурных составляющих; б - их фильтрация

Соотношением (3.22) достаточно точно может охарактеризована работа ряда звеньев реальных каналов связи, например входящих в состав демодуляторов, ограничителей, модуляторов и т. п. Преобразование x(t)→y(t), как правило, однозначно, что не всегда можно сказать об обратном преобразовании y(t)→x(t) (например, квадратичная цепь с характеристикой y = kx²). В силу неприменимости суперпозиции к нелинейным системам рассмотрение сложного воздействия (например, суммы детерминированного и случайного слагаемых) нельзя свести к рассмотрению прохождения каждой из составляющих в отдельности.

При нелинейных преобразованиях возникает трансформация (изменение) спектра входного воздействия. Так, если на вход нелинейной системы воздействует смесь регулярного сигнала и аддитивного шума X(t) = u(t) + N(t) в узкой полосе частот F_c, группирующейся около средней частоты f₀, то в общем случае на выходе будут присутствовать составляющие комбинационных частот трех видов, группирующиеся около частот nf₀ (n = 0, 1,...), продукты биений составляющих входного сигнала между собой (с×с), продукты биений составляющих входного шума (ш×ш); продукты биений сигнала и шума (с×ш). Разделить их на выходе системы обычно невозможно.

Если известны характеристика y = φ(х) нелинейной системы и двумерная функция распределения входного воздействия w(x₁, х₂, t₁, t₂), то основные статистические характеристики выходного процесса, в принципе, всегда можно определить. Так, математическое ожидание отклика

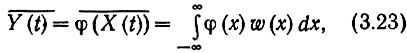
а его корреляционая функция

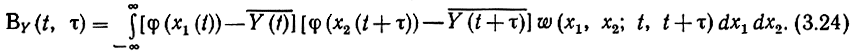
Обратным преобразованием Фурье можно по (3.24) найти и энергетический спектр.

Используя правила нахождения законов распределения для функций от случайных величин (случайных процессов), можно, в принципе, находить и распределение выходного процесса любого порядка, если известно распределение входного процесса. Однако определение вероятностных характеристик отклика нелинейных систем (цепей) даже на стационарные входные воздействия оказывается весьма громоздким и сложным, несмотря на то, что для решения этой задачи разработан ряд специальных приемов. Во многих случаях, особенно для узкополосных сигналов, эти расчеты существенно упрощаются при использовании квазигармонического представления процесса.

В качестве примера рассмотрим прохождение через квадратичный детектор суммы гармонического сигнала s(t) = U₀ cos ω₀t и стационарного квазибелого узкополосного шума n(t) = Х_cn (t) × X cos ω₀t + X_sn sin ω₀t, где X_cn(t), X_sn(t) - не коррелированные квадратурные гауссовские компоненты шума, у которых m_Хсп = m_Xsn = 0, В_Xcn(τ) = В_Xsn(τ) = В(τ), а энергетический спектр равномерен и ограничен полосой частот F_n<<f₀ (В(0) - F_nN₀). Суммарное колебание Z(t) можно представить в виде

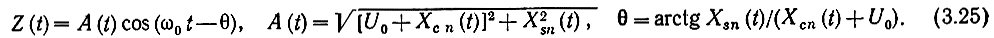
Как известно A(t) имеет обобщенное распределение Рэлея [см. (2.86)]. Отношение сигнал-шум на входе приемника (детектора)

(3.26)

Суммарное колебание на выходе ФНЧ с единичным коэффициентом передачи

Первое слагаемое y_c = U₀²/2 определяет сигнал, остальные - помеху

Математическое ожидание помехи

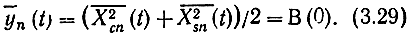
Дисперсия помехи

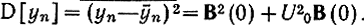
Здесь учтено, что для центрированных гауссовских величин

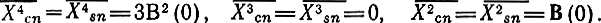
Отношение сигнал-шум на выходе квадратичного детектора

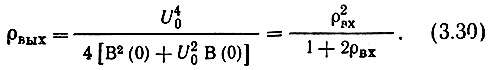
При значениях ρ_вх>>1 имеем

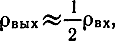
а при малых значениях ρ_вх<<1 - следует ρ_вых≈ρ²_вх.

Превышение сигнал-шум на выходе детектора (приемника) в этой области резко уменьшается с уменьшением ρ_вх. Здесь имеет место подавление слабого сигнала помехой. Так, при ρ_вх = 0,1 имеем ρ_вых = 0,01, т. е. подавление в 10 раз. Этот результат обусловлен некогерентным характером приема сигнала (прием по огибающей), когда не учитываются фазовые отношения сигнала. Хотя приведенное выше рассмотрение относится к гармоническому сигналу, основные выводы могут быть распространены и на модулированные сигналы.