3.3. Прохождение сигналов через случайные каналы связи

Помимо рассмотренных в предыдущем параграфе детерминированных преобразований сигнала, в отдельных звеньях канала (в частности, в линии связи) имеют место и случайные преобразования сигнала. В простейшем случае это преобразование сводится к суммированию сигнала с независимым от него случайным процессом, называемым аддитивной помехой или аддитивным шумом. В более сложных каналах к этому добавляются случайные изменения параметров канала, в результате которых даже в отсутствие аддитивных помех принимаемый сигнал не определяется однозначно передаваемым.

Рассмотрим в общих чертах характерные преобразования сигнала в случайных линейных и нелинейных цепях, а также в цепях с аддитивной помехой.

Случайные линейные цепи. В самом общем виде линейная цепь описывается случайной импульсной реакцией G(t, τ), имеющей тот же смысл, что и g(t, τ) в (3.8), но представляющей случайную функцию двух аргументов: t (момента 'наблюдения реакции) и τ (времени, прошедшего с момента подачи 6-импульса "а вход цепи). Такова, например, импульсная реакция любой линейной цепи, параметры которой подвергаются воздействию случайных внешних влияний, например температуры, давления, влажности и т. д.

Случайную линейную цепь можно характеризовать также случайной передаточной функцией переменных t и ω:

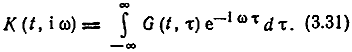
Остановимся на нескольких частных случаях, с которыми чаще всего приводится встречаться. Простейшим является случайный канал, описываемый (3.1), если его параметры k и τ флуктуируют. Обычно такие флуктуации, например в различных проводных линиях связи, вызываются изменениями внешних условий и происходят чрезвычайно медленно^* и в очень небольших относительных пределах. В радиоканалах при прямом распространении, гидроакустических каналах и т. п. флуктуации выражены несколько более заметно.

Из уравнения (3.2) видно, что при передаче по такому каналу узкополосных сигналов с достаточно высокой средней частотой флуктуации времени задержки приводят к флуктуации начальной фазы θ_К сигнала на выходе канала. Важно отметить, что даже при очень малых относительных флуктуациях времени задержки τ начальная фаза может изменяться в очень больших пределах. Для этого необходимо выполнить условие Δτ>>1/f₀, где Δτ - среднеквадратическое отклонена задержки; f₀ - средняя частота сигнала. Это условие в радиоканалах обычно выполняется.

^* (Это значит, что за время длительности "котельниковского интервала" 1/(2F), где F - ширина спектра сигнала, параметры канала не успевают заметно измениться.)

Более сложный случай имеет место, когда сигнал проходит по нескольким параллельным путям от входа канала к его выходу (рис. 3.4), так что на выходе каждого пути сигнал имеет вид (3.1), но значения k и τ для разных путей различны и к тому же в небольших пределах флуктуируют.

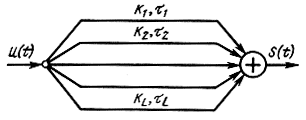
Рис. 3.4. Многопутевое распространение сигнала

Такого рода многопутевое распространение сигнала характерно для большинства радио-, гидроакустических и некоторых других каналов. Энергия волны распространяется обычно в неоднородной среде и испытывает отражения от различных неоднородностей. Эти неоднородности могут быть распределены внутри относительно небольшого отражающего (рассеивающего) объема. В этом случае разности хода (разности значений τ) для отдельных путей невелики. Если по такому каналу направить очень короткий импульс, то и на его выходе импульс будет довольно коротким. Такой канал принято называть однолучевым. Наличие разных путей ("подлучей", как их иногда называют) не вызывает в этом случае существенного рассеяния (растяжения) сигнала во времени, но приводит к возникновению явления замираний, которое заключается в более или менее быстрых случайных изменениях передаточной функции канала (мультипликативная помеха).

Для пояснения замираний рассмотрим передачу по каналу (см. рис. 3.4) гармонического сигнала с единичной амплитудой u(t) = Re e^itω. На выходе сигнал

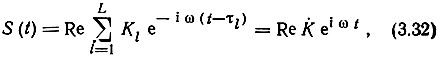
где L - число путей (подлучей, попадающих в точку приема); K_l - коэффициент передачи по l-му подлучу; τ_l - время распространения l-то подлуча;

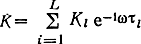
- комплексная амплитуда выходного сигнала, которая в данном случае по определению равна передаточной функции канала.

Передаточная функция в общем случае зависит от частоты ω. Если учесть, что вследствие хаотических перемещений отражателей значения K_l и τ_l флуктуируют, то К зависит также от времени, представляя собой случайную функцию (мультипликативную помеху) K(t, iω). Во многих случаях эта функция флуктуирует значительно быстрее , чем величины K_l и τ_l.

Важной характеристикой канала с замираниями является распределение вероятностей комплексной передаточной функции K̇(t, iω) и, в первую очередь, ее модуля |K̇|. Для определения этого распределения представим K(t, iω) в следующем виде:

где K = |K̇| и θ_K - соответственно модуль и аргумент передаточной функции, которые также являются случайными функциями t и ω, а Х = K cos θ_K и Y = K sin θ_K - квадратурные составляющие.

С другой стороны, согласно (3.32)

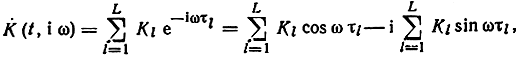
откуда

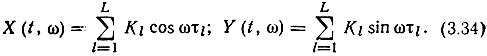
Поскольку X и Y образуются в результате сложения большого числа слаба коррелированных величин с ограниченными дисперсиями, к ним обычно можно применить центральную предельную теорему и считать их нормально распределенными.

Для случая, когда все K_l одного порядка и фазовые сдвиги достаточно велики, легко показать, что X и Y имеют одинаковые дисперсии σ², а их математические ожидания m_Х = m_Y = 0. В этом случае одномерное распределение вероятностей |K| является рэлеевским:

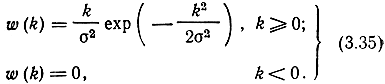
Это доказывается в точности так, как было сделано в § 2.4 при выводе формулы (2.76). Фаза результирующего сигнала θ_K при этом распределена равномерно на интервале (0; 2π). Дисперсия квадратурных составляющих σ² равна; средней мощности приходящего сигнала. Такие замирания, как и каналы, в которых они проявляются, называются рэлеевскими.

Во многих каналах замирания отличаются от рэлеевских. Иногда в одному из подлучей коэффициент передачи k_l значительно больше, чем в других, и можно считать, что помимо диффузно отраженных подлучей в место приема приходит и регулярный (незамирающий) луч. В этом случае коэффициент передачи канала

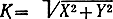
подчиняется обобщенному распределению Рэлея (см. (2.86)):

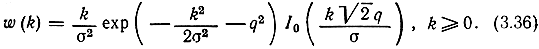
Здесь q² = (m²_Х + m²_Y/2σ² - отношение мощностей регулярной и флуктуирующей составляющих.

В общем случае, когда σ²_X ≠ σ²_Y получается так называемое четырех параметрическое распределение модуля и фазы замирающего сигнала. Соответствующие плотности вероятностей даны в [6].

Если по однолучевому каналу с замираниями передается относительно узко-полосный сигнал, а среднеквадратическое отклонение запаздывания Δτ в отдельных подлучах удовлетворяет условию

где F - ширина спектра сигнала, то изменения начальных фаз на разных частотах со в спектре сигнала, равные ωΔτ, почти одинаковы. При этом все составляющие спектра сигнала замирают "дружно", т. е. их амплитуда и фазы изменяются одинаково. Такие замирания называют общими, или гладкими^*. Если же условие (3.37) не выполнено, то в разных областях спектра сигнала процессы замирания не совпадают (селективные замирания). При этом наблюдаются существенные изменения формы сигнала, что характерно для многолучевых каналов радиосвязи.

^* (Заметим, что условие (3.37) может выполняться при Δτ>>1/f₀, так как радиоканалах f₀>>F.)

Быстрота изменений во времени комплексного случайного процесса K(t, iω) = X(t, ω)+ iY(t, ω) (при фиксированной частоте), или, как говорят, скорость замираний сигнала характеризуется временем корреляции τ_K квадратурных компонент X(t, ω) и Y(t, ω) или шириной энергетического спектра замираний Δf_Зам = 1/τ_K.

Нелинейные преобразования в канале. Среда, в которой распространяются радиосигналы, а также проводные линии связи обладают высокой степенью линейности. Почти все нелинейные искажения, наблюдаемые в некоторых каналах, вызываются входящей в состав канала аппаратурой, в частности, выходными каскадами передатчика, входными каскадами приемника и промежуточными усилителями (ретрансляторами).

Промежуточные усилители можно разделить на два типа - линейные (аналоговые) и нелинейные (цифровые). И те, и другие применяются как в проводной, так и в радиорелейной связи. Аналоговые ретрансляторы проектируются так, чтобы обеспечить весьма высокую степень линейности. Это достигается применением глубокой отрицательной обратной связи в усилителях, позволяющей снизить коэффициент гармоник до сотых долей процента. Это очень существенно для широкополосных каналов, в которых передается одновременно много сообщений с частотным разделением (см. гл. 9), так как нелинейность в этом случае приводит к взаимным (переходным) помехам.

В каналах, называемых цифровыми, все или часть ретрансляторов содержат демодулятор и модулятор, которые, как правило, нелинейны по самому принципу действия. На каждом участке между ретрансляторами сигнал искажается аддитивными и мультипликативными помехами, но если длина участка невелика, эти искажения не настолько значительны, чтобы привести к ошибочной демодуляции. Поэтому демодулятор ретранслятора восстанавливает с вероятностью, очень близкой к 1, дискретный сигнал, действовавший на входе предыдущего модулятора. Это позволяет вновь сформировать непрерывный сигнал таким же, каким он был сформирован в передающем устройстве. Такие нелинейные ретрансляторы называют регенераторами (восстановителями).

Если канал с линейными ретрансляторами (рис. 3.5,а) можно рассматривать как последовательное соединение нескольких непрерывных каналов, канал с регенераторами (рис. 3.5,6) является последовательным соединением нескольких дискретных каналов. В состав каждого из них входят модулятор, непрерывный канал (среда, линия) и демодулятор.

Аддитивные помехи в канале связи вызываются весьма различными причинами и могут принимать самые различные формы, индивидуальные реализации которых трудно учесть. Именно эти помехи чаще вызывают необратимые преобразования передаваемых сигналов. Как указывалось в гл. 1, несмотря на большое разнообразие, аддитивные помехи по их электрической и статистической структуре разделяют на три основных класса: флуктуационные (распределенные по частоте и времени), сосредоточенные по частоте (квазигармонические) и сосредоточенные во времени (импульсные). Следует еще раз подчеркнуть, что с точки зрения передачи информации по каналу существен не вид преобразования сигнала, а то, являются ли эти преобразования обратимыми или необратимыми. Последние влекут за собой потери информации.

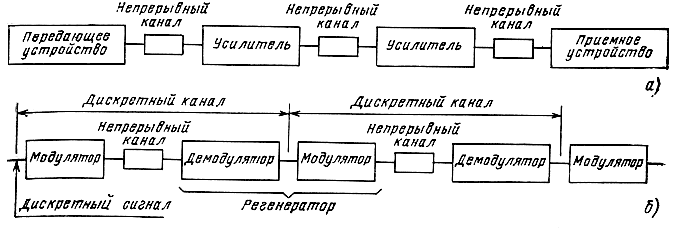
Рис. 3.5. Структурная схема канала связи с ретрансляторами: а - линейными; б - нелинейными (регенераторами)

В отсутствие аддитивных помех детерминированные линейные преобразования сигнала чаще всего обратимы. В присутствии даже очень слабой аддитивной помехи линейные преобразования оказываются необратимыми.

С физической точки зрения аддитивные флуктуационные помехи порождаются в системах связи различного рода флуктуациями, т. е. случайными отклонениями тех или иных физических величин (параметров) от их средних значений. Так, источником шума в электрических цепях могут быть флуктуации тока, обусловленные дискретной природой носителей заряда (электронов, ионов). Дискретная природа электрического тока проявляется в электронных лампах и полупроводниковых приборах в виде дробового эффекта.

Флуктуационные помехи являются гауссовскими случайными процессами (см. гл. 2), которые чаще всего считаются стационарными с нулевыми средними значениями.

Сумма большого числа любых помех от различных источников,, вследствие условий центральной предельной теоремы теории вероятностей, также имеют характер флуктуационной помехи. Многие помехи при прохождении через приемное устройство часто приобретают свойства нормальной флуктуационной помехи (см. § 3.2).

Наиболее распространенной причиной шума в аппаратуре связи являются флуктуации, обусловленные тепловым движением. Случайное тепловое движение носителей заряда в любом проводнике вызывает случайную разность потенциалов (напряжения) на его концах. Среднее значение напряжения равно нулю, а переменная составляющая проявляется как шум. Тепловой шум на входе приемника представляет собой гауссовский случайный процесс с нулевым средним и энергетическим спектром (спектральной (плотностью):

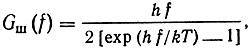
где h≈6,6×10^-34 Дж×с - постоянная Планка; k = 1,38×10^-23Дж/град - постоянная Больцмана; Т - абсолютная температура источника шума; f - текущая частота.

В диапазоне звуковых и радиочастот N₀ = kT и поэтому постоянна спектральная плотность

Величина N₀ = kT является односторонней (на положительных частотах) спектральной плотностью шума.

В диапазоне оптических частот, который с развитием квантовой электроники становится весьма перспективным для связи, hf>>kT и тепловой шум оказывается очень слабым. Однако в этом диапазоне при слабых сигналах существенное значение имеет "квантовый шум", вызванный дискретной природой излучения сигнала. Сущность квантового шума, который не аддитивен, ибо коррелирован с сигналом, связана с соотношением неопределенности, согласно которому среднеквадратические ошибки при измерении энергии фотона σ_Е и времени его прихода σ_t подчиняются неравенству σ_Eσ_t≥h. Поэтому даже при отсутствии аддитивных помех сигнал не может быть принят абсолютно точно. В первом приближении можно рассматривать квантовый шум как помеху со спектральной плотностью, равной энергии фотона hf. В оптическом диапазоне частот f выше 10¹⁵ Гц, поэтому квантовый шум весьма ощутим. В реальных оптических линиях связи помимо квантового шума существуют и другие мешающие факторы, что приводит к необходимости увеличения мощности оптического сигнала.

К сосредоточенным по спектру аддитивным помехам принято относить сигналы посторонних радиостанций, излучения генераторов высокой частоты различного назначения (промышленных, медицинских) и т. п. В общем случае это модулированные колебания, т. е. квазигармонические колебания с изменяющимися параметрами. В одних случаях эти колебания являются непрерывными (например, сигналы вещательных и телевизионных радиостанций), в других - они носят импульсный характер (сигналы радиотелеграфных станций и систем передачи данных). В отличие от флуктуациюнных ширина спектра сосредоточенной помехи в большинстве случаев не превышает полосы пропускания приемника, а в некоторых случаях - она намного уже этой полосы. В диапазоне коротких волн сосредоточенные помехи являются основными, определяющими качество связи, и считаются случайными колебаниями с флуктуациями фаз и амплитуд (замираниями), распределение которых такое же, как и у полезных сигналов.

К импульсным (сосредоточенным во времени) аддитивным помехам принято относить помехи в виде одиночных импульсов, следующих один за другим через такие большие промежутки времени, что переходные явления в приемнике от одного импульса успевают практически затухнуть к моменту прихода следующего импульса. К таким помехам относят многие виды атмосферных и индустриальных помех. Заметим, что "флуктуационная помеха" и "импульсная помеха" являются понятиями относительными. В зависимости от частоты следования импульсов одна и та же помеха может воздействовать как импульсная на приемник с широкой полосой пропускания и как флуктуационная на приемник с относительно узкой полосой пропускания. На практике импульсные помехи приходится рассматривать как случайный, относительно широкополосный (тем шире, чем короче импульсы помехи) процесс, состоящий из отдельных редких, случайно распределенных во времени и по амплитуде импульсов. Статистические свойства таких помех с достаточной для практических целей полнотой описываются распределением вероятностей амплитуд импульсов (которые с весомыми вероятностями могут принимать и весьма большие значения) и распределением временных интервалов между этими импульсами.