3.4. Математические модели каналов связи

Для того чтобы дать математическое описание канала, необходимо и достаточно указать множество сигналов, которые могут быть поданы на его вход, и для любого допустимого входного сигнала задать случайный процесс (сигнал) на его выходе. Задать процесс (см. § 2.1)-это значит задать в той или иной форме распределение вероятностей.

Точное математическое описание любого реального канала обычно весьма сложное. Вместо этого используют упрощенные математические модели, которые позволяют выявить все важнейшие закономерности реального канала, если при построении модели учтены наиболее существенные особенности канала и отброшены второстепенные детали, мало влияющие на ход связи.

Рассмотрим наиболее простые и широко используемые математические модели каналов, начав с непрерывных каналов, поскольку они во многом предопределяют и характер дискретных каналов.

Идеальный канал без помех представляет собой линейную цепь с постоянной передаточной функцией, обычно сосредоточенной в ограниченной полосе частот. Допустимы любые входные сигналы, спектр которых лежит в определенной полосе частот F, имеющие ограниченную среднюю мощность Р (либо пиковую мощность Р_пик). Эти ограничения характерны для всех непрерывных каналов, и в дальнейшем о них не говорится. Заметим, что если мощность сигнала не ограничивать, то множество допустимых сигналов образует векторное пространство, конечномерное (при определенных ограничениях на длительность и ширину спектра) либо бесконечномерное (при более слабых ограничениях). В идеальном канале выходной сигнал при заданном входном детерминированный. Эту модель иногда используют для описания кабельных каналов. Однако, строго говоря, она непригодна для реальных каналов, в которых неизбежно присутствуют, хотя бы и очень слабые, аддитивные помехи.

Канал с аддитивным гауссовским шумом. Сигнал на выходе такого канала

где u(t) - входной сигнал; k и t - постоянные; N (t) - гауссовский аддитивный шум с нулевым математическим ожиданием и заданной корреляционной функцией. Чаще всего рассматривается белый шум либо квазибелый (с равномерной спектральной плотностью в полосе спектра сигнала u(t)).

Обычно запаздывание τ не учитывают, что соответствует изменению начала отсчета времени на выходе канала.

Некоторое усложнение этой модели получается, если коэффициент передачи k и запаздывание т считать известными функциями времени:

Такая модель удовлетворительно описывает многие проводные каналы, радиоканалы при связи в пределах прямой видимости, а также радиоканалы с медленными общими замираниями, при которых можно надежно предсказать значения k, τ.

Канал с неопределенной фазой сигнала отличается от предыдущего тем, что в нем запаздывание является случайной величиной. Для узкополосных сигналов, с учетом (2.69) и (3.2), выражение (3.39) при постоянном k и случайных τ(t) можно представить в виде

где ũ(t) - преобразование Гильберта от u(t); θ_K = ω₀τ - случайная начальная фаза. Распределение вероятностей θ_K предполагается заданным, чаще всего равномерным на интервале от 0 до 2π. Эта модель удовлетворительно описывает те же каналы, что и предыдущая, если фаза сигнала в них флуктуирует. Такая флуктуация вызывается небольшими изменениями протяженности канала, свойств среды, в которой проходит сигнал, а также фазовой нестабильностью опорных генераторов.

Однолучевой гауссовский канал с общими замираниями (флуктуациями амплитуд и фаз сигнала) также описывается формулой (3.40), но множитель K, как и фаза θ_K, считаются случайными процессами. Иными словами, случайными будут квадратурные компоненты

При изменении квадратурных компонент X(t), Y(t) во времени принимаемое колебание

Как отмечалось на с. 85, одномерное распределение коэффициента передачи K(t) может быть рэлеевским (3.35) или обобщенным рэлеевским (3.36). Такие каналы называют соответственно каналами с рэлеевскими или с обобщенными рэлеевскими замираниями. В рамках общей гауссовской модели канала [6] K(t) имеет четырех параметрическое распределение. Модель однолучевого канала с замираниями достаточно хорошо описывает многие каналы радиосвязи в различных диапазонах волн, а также некоторые другие каналы.

Канал с межсимвольной интерференцией (МСИ) и аддитивным шумом. Эта модель является частным случаем (3.31), когда G(t, τ) от t не зависит (или меняется очень медленно), так что рассеяние по частоте практически не наблюдается.

Межсимвольная интерференция вызывается рассеянием сигнала во времени при его прохождении по каналу связи. Она проявляется в том, что на выходе канала сигнал, описываемый общим выражением (3.42), оказывается деформированным так, что одновременно присутствуют отклики канала на отрезки входного сигнала, относящиеся к довольно отдаленным моментам времени. При передаче дискретных сообщений это приводит к тому, что при приеме одного символа на вход приемного устройства воздействуют также отклики на более ранние (а иногда и более поздние) символы, которые в этих случаях действуют как помехи.

Межсимвольная интерференция непосредственно вызывается нелинейностью фазо-частотной характеристики канала и ограниченностью его полосы пропускания. В радиоканалах причиной МСИ чаще всего является многолучевое распространение радиоволн^*.

^* (Использование сигналов с большой базой позволяет в месте приема ликвидировать вредные последствия многолучевого распространения, однако такие системы характеризуются низкой эффективностью использования полосы частот канала.)

Пусть передатчик передает синхронно с тактовым интервалом Т последовательность элементарных сигналов, соответствующих цепочке символов

причем каждый из символов последовательности выбирают из возможного для данного кода набор 0, 1, ..., m - 1 (m - основание кода).

Обозначим отклик линейного канала на элементарный сигнал, соответствующий символу b_r через s_r(t)^*, 0≤t≤(Q + 1)T, где

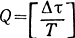
относительная память канала, определяемая целой частью от деления времени рассеяния канала Δτ (длительности переходного процесса в канале) на Т. Тогда принимаемое колебание z(t) в месте приемка на интервале анализа T_a = (D+1T)^** при поиске решения о символе b₀ можно записать в виде

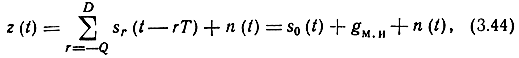
где s₀(t) - сигнал, обусловленный анализируемым символом

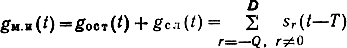
сигнал межсимвольной интерференции, обусловленный символами, переданными до и после анализируемого символа; n(t)-аддитивный шум в канале;

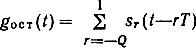
сигнал, который определяет остаточный сигнал, МСИ, обусловленный символами, переданными до анализируемого;

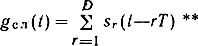
- сигнал, который определяет сигнал МСИ, обусловленный символами, переданными после анализируемого. Чем больше скорость передали символов 1/Т в каждом частотном канале при заданной его полосе пропускания, тем большее число соседних с анализируемым символов определяет сигнал g_M.u(t). В некоторых случаях в модели (3.44) можно считать, что элементарные сигналы на приеме s_r(t) и передаче u_r (t) связаны детерминированными (как правило, линейным) отношением. Тогда при незначительном уровне шумов n(t) в канале можно, в принципе, осуществить его коррекцию, т. е. перейти к модели не искажающего канала. Однако при значительных уровнях шумов в канале с МСИ предельное качество может обеспечить лишь оптимальный прием [8]. При случайных изменениях параметров канала функции s_r(t) (G(t, τ)) становятся случайными и модель (3.44) усложняется.

^* (При использовании двоичных противоположных сигналов и постоянных параметрах канала s_r(t) = a_rs(t), где s(t)-отклик канала на элементарный сигнал, соответствующий символу 1, a_r = ±1.)

^** (При поэлементном приеме D определяет задержку (выраженную в числе символов) принятия решения о передаваемом символе. С ростом D возрастает качество связи при оптимальном приеме. Обычно выбирают D≤Q [8].)

^*** (При Т_a = Т (D = 0) это слагаемое сигнала МСИ обращается в нуль.)

Модели дискретного канала. Полезно напомнить, что в дискретном канале всегда содержится непрерывный канал, а также модем. Последний можно рассматривать как устройство, преобразующее непрерывный канал в дискретный. Поэтому, в принципе, можно вывести математическую модель дискретного канала из моделей непрерывного канала и модема. Такой подход часто является плодотворным, однако он приводит к сложным моделям.

Рассмотрим простые модели дискретного канала, при построении которых свойства непрерывного канала и модема не учитывались. Следует, однако, помнить, что при проектировании системы связи имеется возможность варьировать в довольно широких пределах модель дискретного канала при заданной модели непрерывного канала изменением модема.

Модель дискретного канала содержит задание множества возможных сигналов на его входе и распределение условных верояткостей выходного сигнала при заданном входном. Здесь входным и выходным сигналами являются последовательности кодовых символов. Поэтому для определения возможных входных сигналов достаточно указать число га различных символов (основание кода), а также длительность Т передачи каждого символа. Будем считать значение Т одинаковым для всех символов, что выполняется в большинстве современных каналов. Величина v = 1/T определяет количество символов, передаваемых в единицу времени. Как указывалось в § 1.5, она называется технической скоростью и измеряется в бодах. Каждый символ, поступивший на вход канала, вызывает появление одного символа на выходе, так что техническая скорость на входе и выходе канала одинакова^*.

^* (В реальных каналах это не всегда выполняется, так как при нарушении тактовой синхронизации модема число символов на выходе канала может оказаться больше или меньше, чем на входе. В данном курсе это обстоятельство не учитывается и синхронизация считается идеальной. Методы обеспечения синхронизации изучаются в специальных курсах.)

В общем случае для любого n должна быть указана вероятность того, что при подаче на вход канала любой заданной последовательности b^[n] кодовых символов, на выходе появится некоторая реализация случайной последовательности B^[n]. Кодовые символы обозначим числами от 0 до m-1, что позволит производить над ними арифметические операции. При этом все n-последовательности (векторы), число которых равно mⁿ, образуют mⁿ-мерное конечное векторное пространство, если "сложение" понимать как поразрядное суммирование по модулю m и аналогично определить умножение на скаляр (целое число). Для частного случая m = 2 такое пространство было рассмотрено в § 2.6.

Введем еще одно полезное определение. Будем называть вектором ошибки поразрядную разность (разумеется, по модулю m) между принятым и переданным векторами. Это значит, что прохождение дискретного сигнала через канал можно рассматривать как сложение входного вектора с вектором ошибки. Вектор ошибки играет в дискретном канале примерно ту же роль, что и помеха в непрерывном канале. Таким образом, для любой модели дискретного канала можно записать, пользуясь сложением в векторном пространстве (поразрядным, по модулю m):

где B^[n] и В^[n] - случайные последовательности из n символов на входе и выходе канала; Е^[n] - случайный вектор ошибки, который в общем случае зависит от В^[n] Различные модели отличаются распределением вероятностей вектора E^[n]. Смысл вектора ошибки особенно прост в случае двоичных каналов (m = 2), когда его компоненты принимают значения 0 и 1. Всякая единица в векторе ошибок означает, что в соответствующем месте передаваемой последовательности символ принят ошибочно, а всякий нуль означает безошибочный прием символа. Число ненулевых символов в векторе ошибок называется его весом. Образно говоря, модем, осуществляющий переход от непрерывного канала к дискретному, преобразует помехи и искажения непрерывного канала в поток ошибок.

Перечислим наиболее важные и достаточно простые модели дискретных каналов.

Симметричный канал без памяти определяется как дискретный канал, в котором каждый переданный кодовый символ может быть принят ошибочно с фиксированной вероятностью р и правильно с вероятностью 1-р, причем в случае ошибки вместо переданного символа b может быть с равной вероятностью принят любой другой символ. Таким образом, вероятность того, что принят символ b̂_j, если был передан b_i

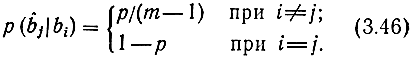
Термин "без памяти" означает, что вероятность ошибочного приема символа не зависит от предыстории, т. е. от того, какие символы передавались до него и как они были приняты. В дальнейшем, для сокращения, вместо "вероятность ошибочного приема символа" будем говорить "вероятность ошибки".

Очевидно, что вероятность любого n-мерного вектора ошибки в таком канале

где l - число ненулевых символов в векторе ошибки (вес вектора ошибки)^*. Вероятность того, что произошло l каких угодно ошибок, расположенных как угодно на протяжении последовательности длины n, определяется формулой Бернулли

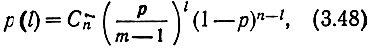
где

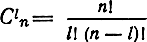
биномиальный коэффициент, равный числу

различных сочетаний l ошибок в блоке длиной n.

^* (В двоичным канале вес вектора совпадает с его нормой, определяемой (2.104).)

Эту модель называют также биномиальным каналом. Она удовлетворительно описывает канал, возникающий при определенном выборе модема, если в непрерывном канале отсутствуют замирания, а аддитивный шум белый (или, по крайней мере, квазибелый). Вероятности переходов в двоичном симметричном канале схематически показаны в виде графа на рис. 3.6.

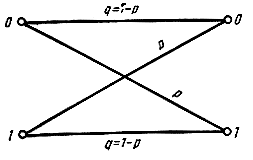
Рис. 3.7. Переходные вероятности в двоичном симметричном канале со стиранием

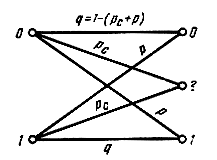
Рис. 3.8. Переходные вероятности в двоичном несимметричном канале

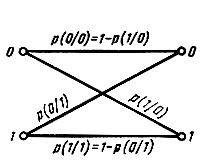
Рис. 3.6. Переходные вероятности в двоичном симметричном канале

Симметричный канал без памяти со стиранием отличается от предыдущего тем, что алфавит на выходе канала содержит дополнительный (m+1)-й символ, обозначаемый знаком "?". Этот символ появляется тогда, когда 1-я решающая схема (демодулятор) не может надежно опознать переданный символ. Вероятность такого отказа от решения или стирания символа р_с в данной модели постоянна и не зависит от передаваемого символа. За счет введения стирания удается значительно снизить вероятность ошибки, иногда ее даже считают равной нулю. На рис. 3.7 схематически показаны вероятности переходов в такой модели.

Несимметричный канал без памяти характеризуется, как и предыдущие {модели, тем, что ошибки возникают в нем независимо друг от друга, однако вероятности ошибок зависят от того, какой символ передается. Так, в двоичном несимметричном (канале вероятность Р(1/0) приема символа "1" при передаче символа "О" не равна вероятности Р(0/1) приема "0" при передаче "1" (рис. 3.8). В этой модели вероятность вектора ошибки зависит от того, какая последовательность символов передается.

Марковский канал представляет собой простейшую модель дискретного канала с памятью. В ней вероятность ошибки образует простую цепь Маркова, т. е. зависит от того, правильно или ошибочно принят предыдущий -символ, но не зависит от того, какой символ передается.

Такой канал, например, возникает, если в непрерывном канале с гауссовским шумом используется относительная фазовая модуляция (см. § 6.5).

Канал с аддитивным дискретным шумом является обобщением моделей симметричных каналов. В такой модели вероятность вектора ошибки Efnl не зависит от передаваемой последовательности. Вероятность каждого вектора ошибки считается заданной и, вообще говоря, не определяется его весом. Во многих каналах из двух векторов с одинаковым весом более вероятным оказывается такой, в котором единицы расположены близко друг к Другу, т. е. имеется тенденция к группированию ошибок.