4.2. Взаимная информация

Энтропия ансамбля характеризует среднее количество полной информации, содержащейся в сообщении. Определим теперь информацию, содержащуюся в одном ансамбле относительно другого, например, в принятом сигнале относительно переданного сообщения. Для этого рассмотрим объединение двух дискретных ансамблей, А и В, вообще говоря, зависимых. Его можно интерпретировать как пару ансамблей сообщений, либо как ансамбли сообщения и сигнала, с помощью которого сообщение передается, либо как ансамбли сигналов на входе и выходе канала связи и т. д. Пусть Р (а_k, b_l) - совместная вероятность реализаций а_k и b_l Совместной энтропией ансамблей А и В будем называть

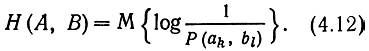
Введем также понятие условной энтропии

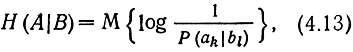
где P(a_k|b_l) - условная вероятность а_k, если имеет место b_l; здесь математические ожидания берутся по объединенному ансамблю АВ. В частности, для источников без памяти

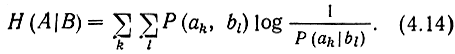
Из теоремы умножения вероятностей Р(а, b) = Р(а)Р(b|а) = Р(b)Р(а|b) следует, что

Для условной энтропии справедливо двойное неравенство

При этом равенство Н(А|В) = 0, как видно из (4.13), имеет место в том случае, когда при каждом значении b_l условная вероятность одной реализации Р(a_i|b_l) = 1, а для всех остальных реализаций Р(a_k|b_l) = 0. Это означает, что, зная реализацию В, можно точно установить реализацию А. Другими словами, В содержит полную информацию об А.

Другой крайний случай, когда Н(А|В) = Н(А) имеет место, если Р(a_k|b_l) = Р(а_k) при всех а и b. Последнее равенство означает, что события А и В независимы. В этом случае знание реализации В не уменьшает неопределенности А, т. е. В не содержит никакой информации об А.

В общем случае условная энтропия Н(А|В) меньше безусловной Н(А) и знание реализации В снижает в среднем первоначальную неопределенность А. Естественно назвать разность Н (А) - Н(А|В) количеством информации, содержащейся в В относительно А. Ее называют также взаимной информацией между А и В и обозначают I(А, В):

Подставляя в (4.17) (4.3) и (4.13), выразим взаимную информацию через распределения вероятностей:

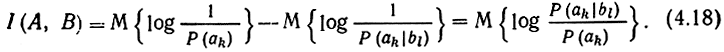
Если воспользоваться теоремой умножения Р(а_k, b_l) = Р (b_l) Р (a_k|b_l), то можно записать I (А, В) в симметричной форме:

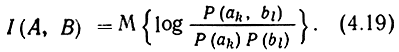
Взаимная информация измеряется в тех же единицах, что и энтропия, например в битах. Величина I(А, В) показывает, сколько в среднем получаем бит информации о реализации ансамбля А, наблюдая реализацию ансамбля В.

Сформулируем основные свойства взаимной информации:

1.

причем равенство имеет место тогда и только тогда, когда А и В независимы между собой. Это следует из определения (4.17) и неравенства (4.16).

2.

т. е. В содержит столько же информации относительно А, сколько А содержит относительно В. Это свойство вытекает из симметрии выражения (4.19). Поэтому можно также записать

3.

причем равенство имеет место, когда по реализации В можно однозначно восстановить А. Это следует из (4.16) и (4.17).

4.

причем равенство имеет место, когда по реализации А можно точно установить реализацию В. Это вытекает из (4.21) и (4.23).

5. Полагая в (4.17) В = А и учитывая, что H(A|A) = 0, получим

Это позволяет интерпретировать энтропию источника как его собственную информацию, т. е. информацию, содержащуюся в ансамбле А о самом себе.

Полученные соотношения позволяют взглянуть на сущность энтропии и с других точек зрения. Так, из (4.24) видно, что энтропия ансамбля А представляет собой максимальное количества информации, которое может содержаться в А относительно любого другого ансамбля В. Из (4.17) следует, что для того, чтобы восстановить реализацию ансамбля А в точности, необходимо передать в среднем количество информации, равное энтропии А.

Пусть А - ансамбль дискретных сообщений, а В - ансамбль дискретных сигналов, в которые преобразуются сообщения А. Тогда I(А,В) = Н(А) в том и только в том случае, когда преобразование А→В обратимо. При необратимом преобразовании I(А, В)<Н(А) и разность Н(А)-I(А, В) = Н(А|В) можно назвать потерей информации при преобразовании А→В. Ее называют также ненадежностью. Таким образом, информация не теряется только при обратимых преобразованиях.

Если Т - среднее время передачи одного сообщения, то разделив формулы (4.12) - (4.24) на Т и обозначая

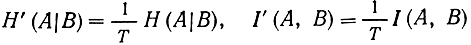
и т. д., получим соответствующие равенства для энтропий и количества информации, рассчитанных не на одно сообщение, а на единицу времени. Величина I'(А, В) называется скоростью передачи информации от А к В (или наоборот).

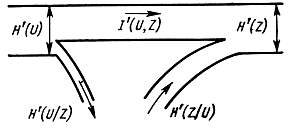
Рис. 4.2. Иллюстрация передачи информации по каналу с помехами

Если, например, U - ансамбль сигналов на входе дискретного канала, a Z ансамбль сигналов на его выходе, то скорость передачи информации по каналу

Эти соотношения наглядно иллюстрирует рис. 4.2. Здесь H'(U) - производительность источника передаваемого сигнала U, a H'(Z) - "производительность" канала, т. е. полная собственная информация в принятом сигнале за единицу времени. Величина H'(U|Z) представляет собой скорость "утечки" информации при прохождении через канал, a H'(Z|U) -скорость передачи посторонней информации, не имеющей отношения к U и создаваемой присутствующими в канале помехами. Соотношение между H'(U|Z) и H'(Z|U) зависит от свойств канала. Так, например, при передаче телефонного сигнала по каналу с узкой полосой пропускания, недостаточной для удовлетворительного воспроизведения сигнала, и с низким уровнем помех теряется часть полезной информации, но почти не получается бесполезной. В этом случае H'(U|Z)>>H'(Z|U). Если же сигнал воспроизводится точно, но в паузах ясно прослушиваются "наводки" от соседнего телефонного канала, то, почти не теряя полезной информации, можно получить много дополнительной, как правило, бесполезной информации и H'(U|Z)<<H'(Z|U).