Глава 4. Основы теории передачи информации

4.1. Информационные параметры сообщений и сигналов

Чтобы сравнивать между собой различные источники сообщений и различные каналы связи, необходимо ввести некоторую количественную меру, позволяющую оценивать содержащуюся в сообщении и переносимую сигналом информацию. Строгие методы количественного определения информации были предложены К. Шенноном в 1948 г. и привели к построению теории информации, являющейся математической основой теории связи, информатики и ряда смежных отраслей науки и техники.

Рассмотрим вначале основные идеи этой теории применительно к дискретному источнику, выдающему последовательность сообщений. Пусть этот источник посылает сообщение а из некоторого ансамбля А (а∈А). Найдем определение количества информации, содержащейся в этом сообщении, исходя из следующих естественных требований:

1. Количество информации должно быть аддитивной величиной, т. е. в двух независимых сообщениях оно должно равняться сумме количества информации в каждом из них.

2. Количество информации в сообщении о достоверном событии равно нулю.

3. Количество информации не должно зависеть от качественного содержания сообщения, в частности, от степени его важности Для получателя, возможных последствий его передачи, эмоциональной окраски и т. д.

Первое требование настолько естественно, что в дополнительных обоснованиях не нуждается. Подчеркнем лишь, что речь идет о независимых сообщениях, когда прием одного из них никак не влияет на восприятие другого. Второе требование также легко понять, поскольку сообщение о достоверном событии не может ничего изменить в наших знаниях. Третье требование быть может не кажется столь очевидным. Однако оно обосновано необходимостью абстрагироваться от различных несущественных деталей, для того чтобы построить достаточно общую теорию. В качестве аналогии можно сослаться на то, что нельзя было бы построить научную механику, если по-разному определять массу тел, состоящих из различных веществ.

Итак, для определения количества информации в сообщении необходимо основываться только на таком параметре, который характеризует в самом общем виде сообщение a из ансамбля А. Таким параметром, очевидно, является вероятность Р (а) того, что источник посылает данное сообщение. Следовательно, количество информации i(a), содержащееся в сообщении а, должно быть функцией от Р(а).

Дальнейшее уточнение искомого определения не составляет труда, если учесть первые два требования. Пусть а₁ и а₂ - два независимых сообщения. Вероятность того, что источник пошлет оба эти сообщения (одно за другим), Р(a₁, а₂) = Р(a₁)Р(а₂), а информация, содержащаяся в них, должна удовлетворять условию аддитивности, т. е. i(a₁, а₂) = i(a₁) + i(a₂). Следовательно, необходимо найти функцию от вероятности Р, обладающую тем свойством, что при перемножении двух аргументов значения функции складываются. Единственная такая функция - это логарифмическая функция i(a) = k log Р (а), где k - любая постоянная, а логарифм берется по любому основанию. Заметим, что при таком определении количества информации выполняется и второе требование - при Р(а) = 1 i(a) = k log 1 = 0.

Что касается выбора коэффициента k и основания логарифма, то они определяются только удобством. Заметим, что изменение основания логарифма также можно свести к изменению коэффициента, поскольку k₁ log_mP(a) = k₂ log_n P(a)log_m n = k₂ logn P(a), так что замена основания логарифма с n на m сводится к умножению коэффициента на log_m n. Поэтому переход от одного основания к другому означает лишь изменение единицы количества информации.

Чтобы количество информации измерялось неотрицательным числом, будем всегда выбирать k = - 1, поскольку Р(а) ≤ 1 и log P(a) ≤ 0 (если основание логарифма больше единицы). Поэтому

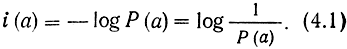
Основание логарифма в (4.1) чаще всего выбирают равным

2. Полученная при этом единица информации носит название двоичная единица, или бит. Она равна количеству информации в сообщении о событии, происходящем с вероятностью 0,5, т. е. таком, которое может с равной вероятностью произойти или не произойти. Такая единица на практике наиболее удобна вследствие широкого использования двоичных кодов в вычислительной технике и связи. В теоретических исследованиях иногда применяют натуральный логарифм, измеряя информацию в натуральных единицах. Натуральная единица в log₂e≈1,443 раза больше двоичной. Мы будем пользоваться в основном двоичными единицами, и в дальнейшем обозначение log будет означать двоичный логарифм.

Итак, количество информации в сообщении тем больше, чем оно менее вероятно, или, иначе, чем оно более неожиданно.

Если источник передает последовательность зависимых между собой сообщений, то получение предшествующих сообщений может изменить вероятность последующего, а следовательно, и количество информации в нем. Оно должно определяться по условной вероятности передачи данного сообщения а_n при известных предшествовавших а_n-1, а_n-2, :

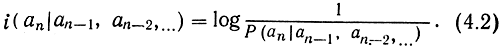
Определенное выше количество информации является случайной величиной, поскольку сами сообщения случайные. Его распределение вероятностей определяется распределением вероятностей сообщений в данном ансамбле. Для характеристики же всего ансамбля (или источника) сообщений используется математическое ожидание количества информации, называемое энтропией и обозначаемое Н(А):

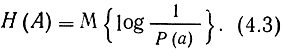
Здесь математическое ожидание, как всегда, обозначает усреднение по всему ансамблю сообщений. При этом должны учитываться все вероятностные связи между различными сообщениями.

Чем больше энтропия источника, тем больше степень неожиданности передаваемых им сообщений в среднем, т. е. тем более неопределенным является ожидаемое сообщение. Поэтому энтропию часто называют мерой неопределенности сообщений. При этом имеется в виду неопределенность, существующая до того, как сообщение передано. После приема сообщения (если оно заведомо принимается верно) всякая неопределенность устраняется. Это позволяет трактовать количество информации как меру уменьшения неопределенности. Можно характеризовать энтропию также как меру разнообразия выдаваемых источником сообщений.

Энтропия является основной характеристикой источника. Чем она выше, тем труднее запомнить (записать) сообщение или передать его по каналу связи. Так, например, далее будет показано, что во многих случаях необходимая затрата энергии на передачу сообщения пропорциональна его энтропии.

Перечислим основные свойства энтропии.

1. Энтропия неотрицательна, она равна нулю только для "вырожденного" ансамбля, когда одно сообщение передается с вероятностью 1, а остальные имеют нулевую вероятность.

2. Энтропия аддитивна. Это значит, в частности, что если рассматривать последовательность из n сообщений как одно "укрупненное" сообщение, то энтропия источника таких укрупненных сообщений будет в n раз больше энтропии исходного источника.

3. Если ансамбль содержит К различных сообщений, то Н(А)≤ log K, причем равенство имеет место только тогда, когда все сообщения передаются равновероятно и независимо. Число К называется объемом алфавита источника.

Свойство 1 вытекает из выражения (4.3), если учесть, что 1/Р(а)≥1 и, следовательно, log(1/P(a))≥0, а математическое ожидание неотрицательной величины не может быть отрицательным. Свойство 2 легко понять исходя из того, что аддитивность была положена в основу определения энтропии. Это соображение, конечно, не является доказательством, однако свойство 2 может быть показано совершенно строго.

Приведем доказательство свойства 3 для источника независимых сообщений. Пусть ансамбль содержит K различных сообщений. Если сообщения передаются статистически независимо друг от друга^* с различными вероятностями, то (4.3) принимает простой вид:

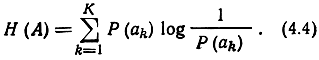
Рассмотрим разность:

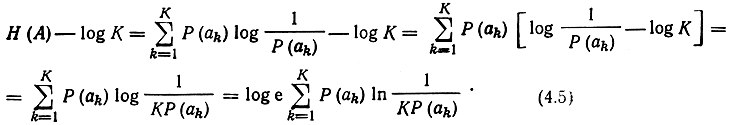
Воспользуемся известным неравенством

справедливым для любого положительного х. Тогда

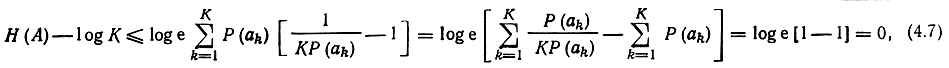
причем равенство имеет место только при КР(а_k) = 1, что и требовалось доказать. Таким образом, максимальная энтропия Н_max(х), возможная при данном объеме алфавита K, равна log K.

^* (Такой источник называется источником без памяти.)

В частности, для двоичного источника без памяти, когда K = 2, энтропия максимальна при Р(а₁) = Р(а₂) =0,5 и равна log 2 = 1 бит. Зависимость энтропии этого источника от Р(а₁) = 1 - Р(а₂) показана на рис. 4.1.

Для источника, сообщения которого образуют простую цепь Маркова, вероятность каждого сообщения а_k целиком определена, если известно переданное непосредственно перед ним сообщение а_i и формула (4.3) принимает следующий вид:

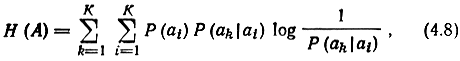
где P(a_k|a_i) обозначает условную вероятность передачи если предыдущим сообщением было а_k, а Р(а_i) - безусловную (среднюю) вероятность передачи а_i. Заметим, что

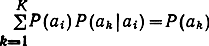
безусловная вероятность сообщения а_k.

Аналогично можно представить энтропию источника зависимых сообщений, если зависимость простирается не только на предыдущее сообщение. В общем случае при любых зависимостях между сообщениями энтропию можно определить из следующих соображений. Рассмотрим последовательность из n сообщений, которую обозначим а^[n]_k. Пусть ее вероятность равна Р(a^[n]_k). Тогда содержащаяся в ней информация, согласно (4.1), равна

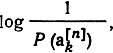
так что на каждое сообщение приходится

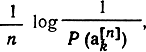
а усреднение по всем таким последовательностям даст

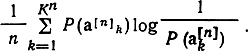
Для устранения влияния предыдущих последовательностей устремим n к бесконечности. Тогда

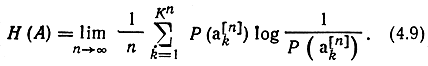
В теории информации доказывается, что энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений при том же объеме алфавита и тех же безусловных вероятностях сообщений.

Пусть, например, источник выдает последовательность букв из алфавита объемом K = 32. Если буквы выбираются равновероятно и независимо друг от друга, то энтропия источника log K = 5 бит. Таким источником могла бы быть обезьяна, нажимающая в хаотическом порядке клавиши пишущей машинки.

Если буквы передаются не хаотически, а составляют связный русский текст, то они оказываются неравновероятными (например, буква А передается значительно чаще, чем Ф) и, главное, зависимыми (так, после гласных не может появиться "ь"; мала вероятность сочетания более трех согласных подряд; вероятность последовательности, не образующей осмысленных слов, практически равна нулю). Если рассматривать ансамбль текстов русской художественной прозы, то энтропия оказывается менее 1,5 бит на букву. Еще меньше, около 1 бит на букву, энтропия ансамбля поэтических произведений, так как в них имеются дополнительные вероятностные связи, обусловленные ритмом и рифмами. Если же рассматривать в качестве источника поток телеграмм, то его энтропия обычно не превышает 0,8 бит на букву, поскольку тексты довольно однообразны.

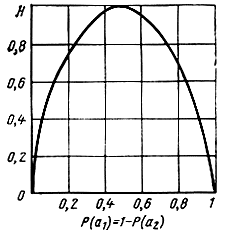
Рис. 4.1. Энтропия двоичного источника без памяти

Величина

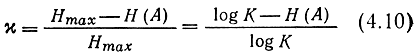
называется избыточностью источника с объемом алфавита K. Она показывает, какая доля максимально возможной при этом алфавите энтропии не используется источником.

Некоторые источники передают сообщения с фиксированной скоростью, затрачивая в среднем время Т на каждое сообщение. Производительностью (в бит на секунду) такого источника Н'(А) назовем суммарную энтропию сообщений, переданных за единицу времени:

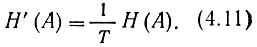
У других источников скорость передачи сообщений определяется самой системой связи. Для таких источников с управляемой скоростью производительность может регулироваться в широких пределах, путем изменения величины Т. Примером источника с фиксированной скоростью является датчик на космическом корабле, передающий каждые 10 с значения температуры, давления воздуха и т. д. Источником с управляемой скоростью является написанный на бумаге текст, подлежащий передаче по телеграфу.