4.6. Теорема кодирования для канала с помехами

Пропускная способность канала, определенная в § 4.5, характеризует потенциальные возможности передачи информации. Они раскрываются в фундаментальной теореме теории информации, известной как основная теорема кодирования К. Шеннона. Применительно к дискретному источнику она формулируется так: если производительность источника сообщений Н(А) меньше пропускной способности канала С:

то существует способ кодирования (преобразования сообщения в сигнал на входе) и декодирования (преобразования сигнала в сообщение на выходе канала), при котором вероятность ошибочного декодирования и ненадежность Н(А|Â) могут быть сколь угодно малы. Если же Н'(А)С, то таких способов не существует.

Таким образом, согласно теореме К. Шеннона конечная величина С - это предельное значение скорости безошибочной передачи информации по каналу. Эта теорема, к сожалению, неконструктивна, т. е. она не указывает конкретного способа кодирования, существование которого доказывается. Тем не менее, значение теоремы трудно переоценить, ибо она в корне изменила воззрения на принципиальные возможности техники связи. До К. Шеннона считалось, что в канале с шумами можно обеспечить сколь угодно малую вероятность ошибки только при неограниченном уменьшении скорости передачи информации. Таков, скажем, путь повышения верности связи за счет повторения символов в канале без памяти.

Например, сообщения двоичного источника а₁ = 0 и а₂ = 1 можно передавать по двоичному симметричному каналу с вероятностью ошибок р<0,5 двумя кодовыми комбинациями, содержащими соответственно n единиц или n нулей:

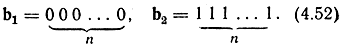
Если в месте приема регистрировать 1 или 0 по большинству этих знаков в кодовой комбинации (мажоритарное декодирование), то ясно, что ошибка произойдет при условии, если в кодовой комбинации неверно будет принято n/2 или более символов. Согласно закону больших чисел вероятность уклонения числа ошибок m в кодовой комбинации длины n от их математического ожидания стремится к нулю при n→∞:

при сколь угодно малом положительном ε.

Поскольку np<n/2 код обеспечит при n→∞ безошибочный прием, однако одновременно при этом и скорость передачи информации по каналу стремится к нулю, тогда как согласно теореме Шеннона существуют коды, которые обеспечивают сколь угодно малую вероятность ошибки при конечной скорости передачи информации.

Обсудим содержание теоремы Шеннона. Как отмечалось в § 4.2, для восстановления по пришедшему сигналу переданного сообщения необходимо, чтобы сигнал содержал о нем информацию, равную энтропии сообщения. Следовательно, для правильной передачи сообщения необходимо, чтобы скорость передачи информации была не меньше производительности источника. Так как по определению скорость передачи информации не превышает значение пропускной способности, но неравенство Н'(А)<C является необходимым условием для точной передачи сообщения. Но является ли это условие достаточным?

Конечно, при С>Н'(А) можно передавать такие сигналы, что I'(В, В) достигнет значения Н'(А). Но I'(В, В) - это скорость передачи информации о сигнале В, а не о сообщении А. Поэтому вопрос сводится к тому, можно ли установить такое соответствие (код) между сообщением А и сигналом В, чтобы вся информация, полученная на выходе канала о сигнале В, была в то же время информацией о сообщении A?

Положительный ответ на этот вопрос очевиден в тривиальном случае, когда в канале нет помех и сигнал В принимается безошибочно. При этом I'(В, B̂) = Н' (В), и если между A и В установлено взаимно-однозначное соответствие, то по принятому сигналу можно однозначно восстановить сообщение. В общем же случае в канале имеются помехи и сигнал В принимается с ошибками, так что I'(В, B̂) < Н'(В). С учетом (4.38) и (4.52) отсюда следует, что Н'(В) > H'(Л).

Это значит, что производительность сигнала В должна быть выше производительности источника сообщения A и, следовательно, В содержит кроме информации об A дополнительную собственную информацию. Часть информации о сигнале В в канале теряется. Вопрос сводится к следующему: можно ли осуществить кодирование так, чтобы терялась только дополнительная (избыточная) часть собственной информации В, а информация об A сохранялась?

Теорема Шеннона дает на этот вопрос почти положительный ответ, с той лишь поправкой, что скорость "утечки информации" (или ненадежность) Н'(А|Â) не равна в точности нулю, но может быть сделана сколь угодно малой. Соответственно сколь угодно малой может быть сделана вероятность ошибочного декодирования. При этом чем меньше допустимая вероятность ошибочного декодирования, тем сложнее должен быть код.

Существует несколько строгих доказательств теоремы Шеннона. Одно из них можно найти в [9]. Все они довольно сложны и поэтому здесь не приводятся. Они основаны на идее случайного кодирования. Для этого рассматривают не какой-либо конкретный код, а множество всех возможных кодов для данного источника и данного канала. Так, например, если канал двоичный, то рассматривают все коды, преобразующие всякую последовательность сообщений длительностью Т в различные последовательности двоичных символов, каждая из которых может быть передана за то же время Т.

Заметим, что если бы двоичный канал был без помех и допускал передачу двоичных символов со скоростью v_К, символ/с, то пропускная способность в расчете на секунду была бы

В этом случае обсуждаемая теорема свелась бы к изложенной выше теореме для источника. Действительно, согласно (4.28), в этом случае можно было бы закодировать последовательность сообщений так, чтобы передавать их со скоростью v_c, сколь угодно близкой к v_k/H(A) сообщений в секунду, т. е. так, чтобы v_cH(A) было как угодно близко к v_K. Но v_cH(A) = Н'(А) по определению, а v_K для канала без помех совпадает с С, так что условие (4.51) сводится к (4.28).

Однако основной интерес представляет более общий случай двоичного канала с помехами. Его пропускная способность С меньше той скорости v_K, с которой поступают на вход канала двоичные кодовые символы. Следовательно, последовательность кодовых символов В, поступающая в канал, должна иметь, в соответствии с теоремой, производительность H'(B)<C<v_к. Это означает, что передаваемые символы не равновероятны и (или) не независимы, т. е. код должен иметь избыточность в отличие от эффективного кода, пригодного для канала без помех. Это значит, что при кодировании сообщений последовательностью кодовых символов используют не все возможные кодовые последовательности.

В этих условиях кодовая последовательность на выходе дискретного канала может не совпадать с той, которая была подана на его вход. Однако она при этом может оказаться (и чаще всего оказывается) одной из тех последовательностей, которые не были использованы при построении кода. Поэтому декодер должен "догадаться", какая кодовая последовательность была послана в канал в действительности. Для этого устанавливают определенные правила декодирования, которые будут частично описаны в гл. 5.

Разумеется, не всегда решение, принимаемое декодером, верное, так что возможна ошибка декодирования, и тогда последовательность сообщений длительностью Т будет принята искаженной, рассмотрим все возможные способы кодирования, т. е. будем разными способами взаимно-однозначно сопоставлять последовательности сообщений A_T длительностью Т с последовательностями кодовых символов В_Т. При таком взаимооднозначном сопоставлении на основании (4.23) и (4.24)

Обозначим скорость передачи информации в канале буквой R - она должна быть практически равна производительности источника:

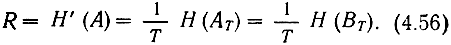
Введем также правило декодирования, называемое правилом максимального правдоподобия (см. подробнее в гл. 5 и 6). Согласно этому правилу принятая на выходе дискретного канала последовательность кодовых символов b̂_T, если она не совпадает ни с одной из использованных при кодировании последовательностей b_T, декодируется как такая последовательность, при передаче которой вероятность принять b̂_T максимальна:

по всем реализациям b_T.

При этих условиях доказывается, что существует функция E(R), зависящая от свойств канала и удовлетворяющая условию

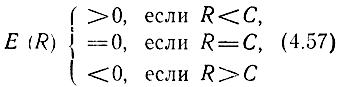
и определяющая верхнюю границу средней вероятности ошибочного декодирования Р_o.д по всем возможным кодам, а именно:

Если это неравенство справедливо для средней вероятности ошибочного декодирования по всем кодам, то существуют такие коды, для которых неравенство (4.58) тем более справедливо.

Функция E(R) называется показателем случайного кодирования. Основание степени 2 связано с тем, что здесь R и С измеряются в битах на секунду. Если бы они измерялись в натуральных единицах, то было бы удобнее применить основание степени е.

Предположим теперь, что задана скорость передачи информации R<C и сколь угодно малая положительная величина δ. Так как при этом E(R)>0, то всегда можно выбрать такое достаточно большое значение T, при котором

Если учесть (4.56), то этим доказана первая часть теоремы Шеннона. Можно также строго доказать вторую часть (обратную теореме кодирования), согласно которой не существует такого кода, при котором неравенство (4.59) могло бы быть выполнено при любом δ в случае R>C.

Теорема кодирования Шеннона справедлива для весьма широкого класса каналов, во всяком случае для всех каналов, которые были описаны в гл. 3, и для всех других каналов, представляющих практический интерес. В частности, она верна и при передаче дискретных сообщений по непрерывному каналу. В этом случае под кодированием понимают отбор некоторого количества реализаций u(t) входного сигнала на интервале Т и сопоставление с каждой из них последовательности элементарных сообщений, выдаваемой источником за тот же интервал Т.

Подчеркнем важный результат, непосредственно следующий из формул (4.57) и (4.58): верность связи тем выше, чем больше Т, т. е. чем длиннее кодируемый отрезок сообщения (а следовательно, и больше задержка при приеме информации), и чем менее эффективно используется пропускная способность канала (чем больше разность С-Н'(А), определяющая "запас пропускной способности" канала). Итак, существует возможность обмена между верностью, задержкой и эффективностью системы. С увеличением Т существенно возрастает сложность кодирования и декодирования (число операций, число элементов и стоимость аппаратуры). Поэтому практически чаще всего предпочитают иметь умеренное значение задержек Т, которые, кстати, не во всех системах связи можно произвольно увеличивать, и добиваются повышения верности за счет менее полного использования пропускной способности канала.

Примеры практического применения кодирования для повышения верности передачи информации будут приведены в последующих главах.