4.7. Информация в непрерывных сообщениях. Эпсилон-энтропия

Источник непрерывных сообщений за конечное время Т может выдать любую из бесконечного множества реализаций некоторого ансамбля сообщений. Вероятность появления некоторой конкретной реализации равна нулю. Если попытаться определить энтропию и производительность такого источника путем предельного перехода, как это было сделано в § 4.4 для непрерывных сигналов, то они окажутся бесконечными.

Смысл этого результата заключается в том, что для передачи непрерывного сообщения с абсолютной точностью нужно было бы передать бесконечно большое количество информации, что, разумеется, невозможно сделать за конечное время, пользуясь каналом с конечной пропускной способностью. Точно также непрерывное сообщение нельзя абсолютно точно запомнить (записать) при наличии сколь угодно слабой помехи.

Тем не менее, как известно, непрерывные сообщения (например, телефонные, телевизионные) успешно передаются по каналам связи с помехами и записываются, например, на магнитную пленку. Это объясняется тем, что на практике никогда не требуется абсолютно точного воспроизведения переданного или записанного сообщения. А для передачи даже с очень высокой, но ограниченной точностью требуется конечное количество информации так же, как и при передаче дискретных сообщений. Разумеется, это количество информации тем больше, чем выше точность, с которой требуется передать (воспроизвести) непрерывное сообщение. Пусть допустимая неточность измеряется некоторым малым параметром ε. То минимальное количество информации, которое требуется передать по каналу связи для воспроизведения непрерывного сообщения с неточностью не более допустимой, академик А. Н. Колмогоров предложил называть ε-энтропией (эпсилон-энтропией) .

Критерий ε, определяющий требуемую точность, может быть каким угодно. Будем называть два варианта сообщения, различающиеся не более, чем на ε, эквивалентными. Это значит, что, если послано одно сообщение, а принято другое, эквивалентное ему, то по данному критерию переданное сообщение считается принятым верно. Так, в системе телефонной связи, если необходимо передать лишь содержание речи, то один и тот же текст, разборчиво прочитанный двумя различными дикторами (например, мужчиной и женщиной), представляет собой эквивалентные сообщения, несмотря на то, что они резко различны даже по спектру. Критерием эквивалентности сообщений здесь является разборчивость речи. При художественных вещательных передачах такой критерий не является приемлемым, ибо в этих случаях существенны и более тонкие характеристики сообщения.

В дальнейшем удобнее будет оперировать не с передаваемым непрерывным сообщением A, а с первичным сигналом В и его реализациями b(i). Дело в том, что непрерывное сообщение А может и не быть функцией времени либо быть функцией нескольких аргументов (например, при телевизионном вещании). Первичный сигнал В (t) в современных системах связи всегда является функцией времени. В тех случаях, когда и сообщение является Функцией времени (например, при телефонной связи), первичный сигнал B(t) точно повторяет функцию A(t) и отличается от сообщения только физической природой [например, А (t) - звуковое давление, B(t) - ток]. Поскольку всегда преобразование сообщения в первичный сигнал обратимо, точность воспроизведения В(t) предопределяет и точность воспроизведения A(t). Поэтому 8 дальнейшем под сообщением будем понимать первичный сигнал B(t), который в большинстве случаев представляет собой центрированный случайный процесс. Его дисперсию (мощность) σ²_В будем считать заданной.

Обеспечение необходимой верности передачи является обязательным требованием к любой системе связи. При передаче дискретных сообщений верность передачи определяется вероятностью правильного приема (или вероятностью ошибки). Такое определение верности можно распространить и на непрерывные сообщения, если понятие "правильно" заменить понятием "эквивалентно". Тогда под верностью передачи непрерывных сообщений будем понимать вероятность того, что принятое сообщение b̂(t) эквивалентно переданному b(t). Чтобы пользоваться таким определением верности, нужно, прежде всего, установить критерий эквивалентности. В ряде случаев этот критерий устанавливают сравнительно легко на основании требований, предъявляемых к степени точности передачи сообщений. Так, например, обстоит дело в телеметрии.

В телефонии верность передачи речевого сообщения оценивают вероятностью того, что получатель правильно поймет смысл переданного и, кроме того, различит особенности голоса. Иначе говоря, два сообщения считаются эквивалентными, если они сохраняют смысл и естественность звучания речи. Такой критерий трудно выразить аналитически, хотя практически эквивалентность реализаций устанавливается несложно. Поэтому и верность передачи чаще определяют экспериментально путем артикуляционных испытаний. Верность передачи речевых сообщений принято выражать разборчивостью фраз, т. е. процентом правильно принимаемых фраз из числа переданных. Кроме разборчивости фраз применяют более строгие критерии - разборчивость слов и слогов.

В некоторых случаях удобно характеризовать эквивалентность сообщений по максимальному абсолютному значению разности

за время длительности сообщений Т_с. Принятая реализация b(t) считается эквивалентной переданной b(t), если указанная разность меньше некоторой заданной величины δ₀. Такой критерий эквивалентности является при некоторых условиях наиболее строгим и поэтому его широко используют в телеметрии, где требуется особая точность восстановления переданной функции.

Наиболее часто применяемым методом определения эквивалентности служит критерий среднего квадрата разности между принятым и переданным сообщениями. При этом мощность передаваемого сообщения b(t) считается заданной. Рассмотрим процесс

представляющий разность между принятым и переданным случайными сообщениями. Его можно назвать шумом воспроизведения. В дальнейшем примем, что

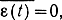
, т. е. регулярная (систематическая) погрешность отсутствует. Сообщения будем называть эквивалентными, если среднеквадратическое отклонение

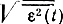
не превышает заданной величины ε₀:

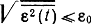
или

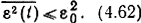
Перейдем к определению ε-энтропии. Взаимная информация I(В, B̂) между двумя не тождественно равными непрерывными сообщениями (сигналами) в общем случае конечна. Будем рассматривать передаваемое сообщение B(t) и множество эквивалентных ему сообщений B̂(t).

Очевидно, количество информации I(В, В̂) зависит не только от статистики процесса B(t), определяющей дифференциальную энтропию h (В) (см. § 4.4), но и от критерия эквивалентности, определяющего условную плотность вероятностей w(b̂|b), а следовательно, и условную энтропию h(B|B̂). Минимальное количество информации, содержащееся в сообщении B̂(t) относительно B(t), при котором они еще эквивалентны, называется эпсилон-энтропией. Согласно (4.32)

где минимум берется по всем условным распределениям w(b̂|b), для которых

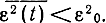
Эпсилон-энтропия определяет количество существенной информации в одном отсчете непрерывного сообщения.

Рассмотрим наиболее простой случай, когда источник непрерывного сообщения (сигнала) гауссовский, т. е. когда сообщение B(t) представляет собой стационарный гауссовский процесс с заданной мощностью Р_В, а критерием эквивалентности является критерий (4.62). Поскольку B(t) = B̂(t)-ε(t), то условная дифференциальная энтропия h(B|B̂) при заданном сообщении B(t) полностью определяется шумом воспроизведения ε(t). Поэтому max h (В|B̂) = max h (ε). Если шум воспроизведения e(t) имеет фиксированную дисперсию

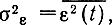
то дифференциальная энтропия h (ε) имеет максимум (4.34) при нормальном распределении

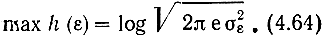
При заданной дисперсии сообщения σ²_В дифференциальная энтропия гауссовского источника h (В) равна

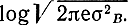
Следовательно, эпсилон-энтропия гауссовского непрерывного источника на один отсчет

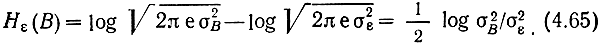
Величина σ²_В/σ²_ε = Р_в/Р_ε характеризует минимальное отношение сигнал-шум, при котором сообщения B(t) и B̂(t) еще эквивалентны. Обозначим это отношение ρ₀. Его значение зависит от характера передаваемых сообщений. Если отдельные отсчеты сообщения независимы, то содержащаяся в них информация складывается.

Производительность источника непрерывных сообщений можно определить как количество информации, которое необходимо передать в единицу времени, чтобы восстановить сообщение при заданном критерии эквивалентности. Если источник выдает независимые отсчеты сообщения (сигнала) дискретно во времени со средней скоростью v, то его эпсилон-производительность

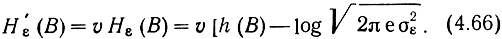
Эпсилон-производительность называют также скоростью создания информации при заданном критерии верности. Для источника непрерывных сообщений, ограниченных полосой F_с, согласно теореме Котельникова шаг дискретизации Δt = 1/v = 1/(2F_c), т. е. необходимое число отсчетов в секунду равно 2F_c. Если спектр сообщения в полосе F_с равномерен, то эти отсчеты некоррелированы (см. § 2.2, пример 4), а для гауссовского источника и независимы. 13 этом случае

Подставив в (4.67) (4.65), получим для гауссовского источника с равномерным спектром в полосе

Из предыдущих рассуждений ясно, что производительность гауссовского источника квазибелого шума (4.68) больше производительности любого другого источника с той же мощностью и той же шириной спектра при том же допустимом шуме воспроизведения Р_ε. Количество информации, выдаваемое гауссовским источником за время Т_с,

Выражение (4.69) совпадает с характеристикой (1.1), названной в § 1.1 объемом сигнала, если D_c = log ρ₀. Это означает, что объем сигнала равен максимальному количеству информации, которая содержится в сигнале длительностью Т_с.

Необходимо подчеркнуть, что шум воспроизведения, в сущности, не является аддитивной помехой. Он не всегда обусловлен шумом в канале, а является результатом различных случайных или регулярных искажений сигнала; иногда он возникает в процессе самой модуляции (см. гл. 8) и в общем случае является просто погрешностью при воспроизведении сообщения.

В соответствии с квадратичным критерием эквивалентности под верностью понимают вероятность того, что сообщение будет принято при отношении мощности сигнала к мощности шума на выходе приемника Р_в/Р_ε не меньше заданной величины ρ₀. Среднеквадратический критерий эквивалентности отвечает практическим запросам в большинстве случаев передачи непрерывных сообщений. Он менее строг, чем критерий максимального абсолютного отклонения, но более строг, чем большинство практических критериев, таких как артикуляционные. Этот критерий удобен и при теоретических исследованиях.

Для канала с пропускной способностью С, на вход которого подключен источник, обладающий производительностью Н'_ε (В), К. Шеннон доказал следующую теорему:

Если при заданном критерии эквивалентности сообщений источника ε²₀ его эпсилон-производительность меньше пропускной способности канала Н'_ε (В) < С, то существует способ кодирования и декодирования^*, при котором неточность воспроизведения сколь угодно близка к ε²₀. При Н'_ε (В)>С такого способа не существует.

^* (Здесь кодирование понимается в широком смысле, как преобразование сообщения в сигнал.)

Теорема Шеннона определяет предельные возможности согласования источника непрерывных сообщений с непрерывным каналом. Оптимальное кодирование непрерывных сообщений (без дискретизации) в непрерывном канале пока не находит приемлемой реализации, хотя имеются определенные успехи в построении устройств, позволяющих существенно сократить избыточность некоторых непрерывных источников. В простейшем случае, когда канал имеет полосу пропускания, охватывающую практически весь спектр сообщения, а уровень аддитивных помех достаточно низок, используется непосредственная передача первичного сигнала В (t) без модуляции. Сигнал в канале S(t) при этом совпадает с В (t). Примером системы связи с непосредственной передачей является телефонная связь в пределах действия одной АТС. Если на выходе канала мощность сигнала Р_с, а мощность помех Р_ш, то при условии Р_с/Р_ш≥ρ₀ воспроизводимое сообщение будет эквивалентно переданному. В общем же случае, как следует из теоремы Шеннона, это условие не обязательно для восстановления сообщения с заданной точностью: необходимо только, чтобы пропускная способность канала превышала эпсилон-производительность источника. При этом условии можно преобразовать сообщение в сигнал так, чтобы отношение мощности Р_в восстановленного сообщения к мощности шума воспроизведения (на выходе приемника) Р_ε было больше ρ₀, хотя в канале (т. е. на входе приемника) отношение Р_с/Р_ш меньше (иногда во много раз), чем ро. Это достигается применением помехоустойчивых видов модуляции (см. гл. 7 и 8).

Вопросы к главе 4

1. Чем определяется количество информации, заключенное в конкретном сообщении?
2. Почему мера количества информации должна логарифмически зависеть от вероятности сообщения?
3. Чему равна энтропия источника дискретных сообщений при равновероятных и независимых сообщениях? Как она изменяется при увеличении объема алфавита?
4. Напишите выражение для энтропии источника при объеме алфавита L и неравных вероятностях элементарных сообщений, полагая, что сообщения выбираются независимо друг от друга.
5. Что называется избыточностью алфавита источника??
6. Определите избыточность алфавита двоичного источника, выдающего сообщения "0" и "1" независимо, с вероятностями р(0)=0,1; р(1)=0,9.
7. Сколько можно составить различных последовательностей из 32 русских букв длиной в 100 букв?
8. * Сколько последовательностей из упомянутых в предыдущем вопросе .составят осмысленный текст или часть осмысленного текста, если считать энтропию русского текста равной 1,5 бит на букву?
9. Оцените производительность телеграфного аппарата, рассматриваемого как источник сообщения, если он работает со скоростью 300 знаков в минуту, передавая произвольный осмысленный русский текст.
10. Изменится ли ответ на предыдущий вопрос, если телеграфный аппарат передает только поздравительные телеграммы?
11. Как изменится ответ на вопрос 9, если аппарат передает цифры в случайной последовательности?
12. Напишите различные выражения для количества информации в В относительно А.
13. Приведите различные определения энтропии источника.
14. Чему равна энтропия источника непрерывных сообщений? Можно ли точно передать непрерывное сообщение по каналу с конечной пропускной способностью?
15. Чем отличается дифференциальная энтропия от обычной энтропии?
16. Вычислите дифференциальную энтропию случайных величин, имеющих плотности вероятностей:
    
    
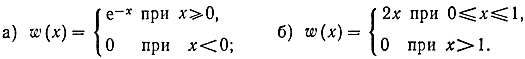
17. * Докажите, что для любой непрерывной случайной величины с дисперсией σ² дифференциальная энтропия
    
    
    причем равенство имеет место только для гауссовской величины.
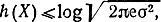
18. Пусть X(t) -процесс с ограниченным спектром шириной F. В преобразователе он заменяется отсчетами, взятыми через интервалы Δt = 1/(2F). Теряется ли при этом информация? Теряется ли информация при квантовании?
19. Дайте определение пропускной способности канала связи.
20. При переводе русского текста на английский язык число букв в среднем уменьшается примерно в 1,3 раза. При переводе того же текста на финский язык число букв возрастает примерно в 1,4 раза. Что можно сказать на основании этого об энтропии данных языков?
21. В каких случаях важно знать пропускную способность канала связи?
22. Чему равна пропускная способность канала связи, составленного из последовательного соединения нескольких каналов с различными пропускными способностями? А при параллельном соединении?
23. Сравните пропускные способности двух дискретных каналов без помех, если в первом канале основание кода m₁ = 2, а во втором канале m₂ = 8, и количество символов, передаваемых в секунду, в первом канале v = 100, а во втором канале v = 40.
24. Сравните пропускные способности тех же каналов, если в них появилась помеха, вызывающая в обоих каналах ошибки с вероятностью р = 0,5. Оба канала при этом симметричны.
25. Как изменяется пропускная способность канала с аддитивным нормальным белым шумом при расширении полосы пропускания канала?
26. Рассмотрите канал (физически неосуществимый), в котором спектральная плотность помехи на некотором конечном участке частот от f_а до f_b точна равна нулю. Чему равна его пропускная способность?
27. Для передачи радиовещательной программы в системе многоканальной связи обычно объединяют несколько телефонных каналов. Почему нельзя для этого воспользоваться одним телефонным каналом?