Глава 5. Основы теории кодирования

5.1. Назначение и классификация кодов

В этой главе рассматривается кодирование сообщений, передаваемых в дискретном канале, или кодирование в узком смысле^*. Дискретный канал образуется из непрерывного путем включения в канал модема. На вход модулятора и с выхода демодулятора поступают дискретные кодовые символы (например, в форме импульсов), одинаковые или различные. Будем обозначать кодовые символы числами 0, 1, ..., m-1, где m - основание кода.

^* (Как уже отмечалось в гл. 1, а также в § 4.3 и 4.6, в широком смысле кодированием называют любое преобразование сообщения в сигнал путем установления взаимного соответствия.)

Пусть источник выдает некоторое дискретное сообщение а, которое можно рассматривать как последовательность элементарных сообщений a_i (i = 1, 2, ..., l). Эти элементарные сообщения будем называть знаками, а их совокупность {а_i} - алфавитом источника. Кодирование заключается в том, что последовательность знаков источника а заменяется кодовым словом, т. е. последовательностью b кодовых символов. Такое преобразование сообщения в кодовое слово (если не учитывать воздействия помех), как правило, является взаимно-однозначным, что и позволяет осуществить декодирование, т. е. восстановить сообщение по принятому кодовому слову.

В простейшем случае, когда объем алфавита источника l равен основанию кода m, можно сопоставить каждый кодовый символ букве источника. Такое кодирование применяют, например, в морском флоте при сигнализации флагами различной формы в Цвета. Чаще применяют более сложные коды, основное назначение которых заключается в согласовании источника сообщений о дискретным каналом по объему алфавита и по избыточности.

Согласование по объему необходимо во всех случаях, когда объем алфавита источника l не совпадает с количеством различных символов m, для передачи которых пригоден используемый дискретный канал. Чаще всего l>m, так что каждый знак источника кодируется несколькими последовательными кодовыми символами. Так, например, в простейшем телеграфном коде Бодо каждая буква русского алфавита кодируется кодовым словом из пяти двоичных символов (0 и 1); в телеграфном коде Морзе на каждую букву алфавита затрачивается от двух до шести символов, принимающих значения "точка", "тире" и "пробел".

Остановимся подробнее на согласовании источника с каналом по избыточности. Пусть случайное сообщение А заменяется кодовой последовательностью В. Поскольку считаем кодирование обратимым, то в соответствии с (4.23) и (4.24)

где I(А, В) - количество информации в кодовой последовательности относительно сообщения; H(А) - энтропия сообщения; H(В) - энтропия кодовой последовательности. Следовательно, энтропия при кодировании не изменяется^*.

^* (Следует обратить внимание на то, что здесь речь идет об энтропии сообщения источника Я (А) и энтропии соответствующей ему последовательности кодовых символов Я (В), а не об энтропии на один символ, которая, конечно, изменяется при изменении объема алфавита. Так, например, если алфавит источника содержит 32 буквы, передаваемые равновероятно и независимо, то H(A) = log 32 = 5 бит. Закодировав их двоичным кодом (m = 2), можно представить каждую букву источника кодовым словом из пяти символов. Энтропия на каждый кодовый символ H(B) = 1 бит, а на все кодовое слово H(В) = = 5 бит = H(A). При кодировании в реальном масштабе времени (т. е. без нарастающих задержек) справедливо равенство производительностей Н'(A) = H'(В) ((см. § 4.3).)

Иначе обстоит дело с избыточностью, определяющей соотношение между энтропией и ее максимальным значением (при данном алфавите). Избыточность может при кодировании как возрастать, так и уменьшаться.

Пусть, например, избыточность источника велика, т. е. H(A)<<H_max(A) = log l. Тогда может стоять задача о таком кодировании, при котором избыточность уменьшается (в предельном случае вовсе устраняется). Эта задача эффективного (или экономного) кодирования уже рассматривалась в § 4.3. Там было показано, что оно позволяет увеличить скорость передачи сообщений по каналу с ограниченной пропускной способностью. В частности, осмысленный русский текст можно передавать, затрачивая всего лишь 1,5 двоичных символов на букву, вместо пяти при примитивном равномерном коде.

Отметим некоторые свойства кодовой последовательности, в которой полностью устранена избыточность. В любом месте такой последовательности все символы появляются равновероятно и независимо от значений других символов. В противном случае энтропия на символ последовательности не имела бы максимального значения log m, т. е. существовала бы остаточная избыточность. Отсюда следует, что и все последовательности символов произвольно заданной длины п равновероятны. Предположим, что при передаче такой кодовой последовательности под воздействием помех возникли ошибки. Принятая ошибочная последовательность кодовых символов соответствует ошибочной последовательности - сообщений, которая, однако, имеет ту же вероятность, что и правильная. Никаких признаков ошибочности принятая последовательность не может иметь. При передаче безызбыточных сигналов по каналу с ошибками любая принятая последовательность соответствует возможному сообщению, но полной уверенности в том, что именно это сообщение передано в действительности, у получателя нет. Ошибочный прием всего лишь одного кодового символа может изменить до неузнаваемости переданное сообщение. Поэтому эффективное кодирование используют в чистом виде только тогда, когда кодовая последовательность не подвергается воздействию помех. Метод построения эффективных неравномерных кодов рассматривается в § 5.2.

Избыточность в передаваемом сообщении позволяет в некоторых случаях обнаруживать и исправлять ошибки. Искаженная кодовая последовательность может иметь нулевую или очень близкую к нулю вероятность, что указывает на наличие ошибки. Если определить, какая из возможных переданных последовательностей наиболее правдоподобна, можно во многих случаях ошибки исправить. Именно так читатель исправляет опечатки в книге "по контексту", а получатель телеграмм догадывается о ее подлинном содержании даже при нескольких ошибочно переданных буквах^*.

^* (Именно необходимость разговаривать при воздействии акустических помех явилась причиной того, что все национальные языки в процессе своего возникновения и развития оказались избыточными и значение избыточности для всех языков близко к χ ≈ 0,70,9.)

Если при кодировании не устранять, а вводить избыточность, то должны увеличиться возможности обнаружения и исправления ошибок. Такое кодирование называют помехоустойчивым, или корректирующим. Ему посвящена основная часть этой главы.

При помехоустойчивом кодировании чаще всего считают, что избыточность источника на входе кодера χ = 0. Для этого имеются следующие основания: во-первых, очень многие дискретные источники (например, информация на выходе ЭВМ) обладают малой избыточностью; во-вторых, если избыточность первичных источников существенна, она обычно порождается сложными связями, которые в месте приема трудно использовать для повышения верности. Разумно поэтому в таких случаях по возможности уменьшить избыточность первичного источника путем эффективного кодирования, а затем методами помехоустойчивого кодирования внести такую избыточность в сигнал, которая позволит достаточно простыми средствами поднять верность. Из сказанного видно, что экономное кодирование вполне может сочетаться с помехоустойчивым.

Теория кодирования за последние 35 лет развивалась весьма интенсивно на основе современных математических методов. В настоящей книге затронуты лишь общие принципы теории кодирования. Вопросы построения используемых на практике кодов, а также технической реализации кодирующих и декодирующих устройств рассматриваются в специальных курсах.

Коды можно классифицировать по различным признакам. Одним из них является основание кода m, или число различных используемых в нем символов. Наиболее простыми являются двоичные (бинарные) коды, у которых m = 2.

Далее коды можно разделить на блочные и непрерывные. Блочными называют коды, в которых последовательность элементарных сообщений источника разбивается на отрезки и каждый из них преобразуется в определенную последовательность (блок) кодовых символов {b_i}, называемую иногда кодовой комбинацией b_l (l = 1, 2, 3, ..., М). Непрерывные коды образуют последовательность символов {b_i}, не разделяемую на последовательные кодовые комбинации: здесь в процессе кодирования символы определяются всей последовательностью элементов сообщения.

В настоящее время на практике чаще используют блочные коды, равномерные и неравномерные. В равномерных кодах, в отличие от неравномерных, все кодовые комбинации содержат одинаковое число символов (разрядов), передаваемых по каналу элементами сигнала неизменной длительности. Это обстоятельство существенно упрощает технику передачи и приема сообщений и повышает помехоустойчивость системы синхронизации. Число различных блоков М я-разрядного равномерного кода с основанием m удовлетворяет очевидному неравенству

Если в (5.2) имеет место равенство, т. е. все возможные кодовые комбинации используются для передачи сообщений, то в этом случае код называется простым, или примитивным. Он не вносит избыточности и поэтому не является помехоустойчивым.

Избыточностью равномерного кода называют, по аналогии с (4.9), величину

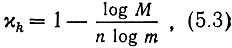
а относительной скоростью кода

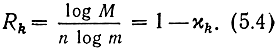
Если все блоки равномерного кода передавать равновероятно и независимо друг от друга, то log M представляет собственную информацию (энтропию), приходящуюся на каждый блок.

В дальнейшем будем рассматривать главным образом двоичные коды (m = 2). Напомним, что множество всех возможных двоичных блоков или кодовых векторов длины п образует линей- иое пространство (см. § 2.6), если под операцией сложения понимать поразрядное сложение по модулю 2, норму определить формулой (2.104), а под расстоянием понимать расстояние Хэмминга (2.105)^*.

^* (Аналогичные дискретные линейные пространства можно построить и для описания недвоичных кодов (m>2).)

Напомним, что расстоянием Хэмминга между двумя кодовыми n-последовательностями, b_i и b_j, которое будем далее обозначать d(i; j), является число разрядов, в которых символы этих последовательностей не совпадают.