5.5. Некоторые разновидности систематических кодов

В поисках более простой техники кодирования и декодирования был найден подкласс линейных систематических двоичных кодов, называемых циклическими и применяемых в технике связи. Название этих кодов связано с тем, что каждый вектор, получаемый из кодового циклической перестановкой его символов, также принадлежит коду. Примером циклического кода является код (7, 4), определяемый матрицами (5.28) и (5.29). Так, например, циклические перестановки вектора 1000101 являются также кодовыми векторами 0001011, 0010110, 0101100 и т. д.

Теория циклических кодов основана на изоморфизме, пространства двоичных n-последовательностей и пространства полиномов степени не выше n-1 вида

где коэффициенты а принимают значения 0 и 1. Множество таких полиномов образует линейное пространство, если определить сложение полиномов как суммирование коэффициентов при соответствующих степенях х по модулю 2. Переменная х является символической, и ее значение не влияет на свойства пространства.

Легко видеть, что между полиномами (5.26) и n-последовательностями имеется изоморфизм, причем полиному (5.26) соответствует n-последовательность α_n-1, α_n-2, ..., α₁, α₀.

Любой полином g(x) степени r<n, который делит без остатка двучлен хⁿ-1, может служить порождающим полиномом циклического (n, k) - кода, где k = n - r. В этот код входят те полиномы (5.26), которые без остатка делятся на g(x). В частности, для кода (7,4) порождающим полиномом является

Среди циклических кодов особое значение имеет класс кодов, предложенных Боузом и Рой-Чоудхури и независимо от них Хоквингемом. Коды Боуза - Чоудхури - Хоквингема (обозначаемые сокращением БЧХ) отличаются специальным выбором порождающего полинома, вследствие чего для них существуют сравнительно просто реализуемые процедуры декодирования. Доказано, что для любой пары натуральных чисел s и t<2^s-2 можно построить двоичный код БЧХ с n = 2^s-1 и k≥n-st, исправляющий любую конфигурацию ошибок с кратностью, меньшей или равной t.

Относительно простой является процедура мажоритарного декодирования, применимая для некоторого класса двоичных линейных, в том числе циклических кодов. Основана она на том, что в этих кодах каждый информационный символ можно несколькими способами выразить через другие символы кодовой комбинации. Если для некоторого символа эти способы проверки дают неодинаковые результаты (одни дают результат "0", а другие - "1", что может быть только в случае ошибочного приема), то окончательное решение по каждому из информационных символов принимается по мажоритарному принципу, т. е. по большинству. Мажоритарное декодирование осуществляется относительно просто, посредством регистров сдвига.

Примером кода, допускающего мажоритарное декодирование, является код (7,3), двойственный рассмотренному ранее коду (7,4). Для него матрица (5.24) является образующей. Ее удобнее записать, переставив столбцы, так:

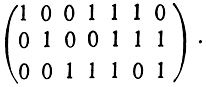
Символ b₁ в этом коде связан с другими символами следующими соотношениями: b₁ = b₂ + b₆ = b₇ + b₅ = b₃ + b₄. Обозначим принятые после демодуляции b̂₁, b̂₂, b̂₃, b̂₄, b̂₅, b̂₆, b̂₇. Если бы они все были приняты верно, то для переданного символа были бы верны следующие четыре равенства (проверки):

Каждый из символов принятого блока входит только в одну из этих проверок для b₁. Код, для которого выполняется это условие, называется кодом с разделенными проверками.

Предположим, что один из символов блока принят с ошибкой. Тогда три из проверок (5.28) дадут одно (правильное) значение b₁, а одна проверка, в которой участвует ошибочный символ, даст другое, ошибочное значение. Принимая решение по большинству, получим правильное значение b₁. Если бы ошибок было три или больше, то мажоритарное решение могло бы дать ошибочный результат. При двух ошибочно принятых символах может получиться одинаковое (верное) значение для b₁ во всех проверках (например, при ошибочно принятых b̂₂ и b̂₆) либо в двух проверках b₁ = 0, а в двух других b₁ = 1 (например, при ошибочно принятых b̂₂ и b̂₁). В последнем случае можно только констатировать наличие ошибок.

После принятия решения о символе b₁ аналогично проверяют значения b₂ и b₃. Поскольку рассматриваемый код (7, 3) - циклический, соответствующие проверки получаются из (5.28) циклической перестановкой.

Мощные коды (т. е. коды с длинными блоками и большим кодовым расстоянием d) при сравнительно простой процедуре декодирования можно строить, объединяя несколько коротких кодов. Так строится, например, итеративный код из двух линейных систематических кодов (n₁, k₁) и (n₂, k₂). Вначале сообщение кодируется кодом 1-й ступени (n₂, k₂). Пусть k₂ блоков кода 1-й ступени записаны в виде строк матрицы. Ее столбцы содержат по k₂ символов, которые будем считать информационными для кода 2-й ступени (n₂, k₂) и подпишем к ним n₂-k₂ проверочных символов. В результате получится блок (матрица n₁×n₂), содержащий n₁n₂ символов, из которых k₁k₂ являются информационными:

Процесс построения кода можно продолжить в 3-м измерении и т. д.

При декодировании каждого блока 1-й ступени обнаруживают и исправляют ошибки. После того как принят весь двумерный блок, вновь исправляют ошибки и стирания, но уже по столбцам, кодом 2-й ступени, причем приходится исправлять только те ошибки, которые не были исправлены (или были ложно "исправлены") кодом 1-й ступени. Легко убедиться, что минимальное кодовое расстояние для двумерного итеративного кода d = d₁d₂, где - d₁ и d₂ - соответственно минимальные кодовые расстояния для кодов 1-й и 2-й ступеней.

На итеративный код похож каскадный код, но между ними имеется существенное различие. Первая ступень кодирования в каскадном коде осуществляется так же, как в итеративном. Однако после того, как сформированы k₂ строк - блоков кода (пи k₁) 1-й ступени (внутреннего), они не делятся на столбцы. Каждая последовательность из k\ двоичных (информационных) символов внутреннего кода рассматривается как один символ недвоичного кода 2-й ступени (внешнего). Основание этого кода m = 2^k₁. К этим символам приписывается еще n₂-k₂ проверочных символов m-ичного кода, также в виде строк длиной k₁. К каждой из этих строк приписываются двоичные проверочные символы, в соответствии с внутренним кодом (n₁, k₁). В результате образуется такая же матрица, как при итеративном двумерном коде. При приеме сначала декодируются (с обнаружением или исправлением ошибок) все строки (блоки внутреннего кода), а затем декодируется блок внешнего m-ичного кода (n₂, k₂), причем исправляются ошибки и стирания, оставшиеся после декодирования внутреннего кода. В качестве внешнего кода используют обычно m-ичный код Рида - Соломона, обеспечивающий наибольшее возможное d при заданных n₂ и k₂, если n₂<m. Каскадные коды во многих случаях наиболее перспективны среди известных блочных помехоустойчивых кодов.

Все операции с матрицами и полиномами над конечным полем, составляющие процедуру кодирования и декодирования, осуществляются средствами вычислительной техники. Для коротких систематических кодов они довольно просты и выполняются с помощью триггеров, объединенных в цепочки (регистры сдвига) и логические схемы. С увеличением длины кода эти операции усложняются. Хотя благодаря особой алгебраической структуре кодов БЧХ сложность растет медленно, тем не менее, при использовании эффективных длинных кодов (n>>100) приходится применять в качестве декодера микропроцессор и даже ЭВМ, специализированную или универсальную.

Примером не блочного кода, используемого в технике связи, может служить рекуррентный, или цепной код. Это непрерывный код. В простейшем его варианте информационные символы чередуются с проверочными, образуя последовательность

где b_l - l-й информационный символ, принимающий значение 0 или 1 в соответствии с передаваемым сообщением, а b_l,k+1 - проверочный символ, определяемый уравнением

причем сложение производится по модулю 2.

Цепной код, содержащий на n символов k информационных, часто обозначают (k/n), в частности, код (5.29) обозначают (1/2). Ошибка при приеме одного информационного символа b_i приводит к тому, что (5.30) не выполняется для двух проверочных символов: b̂_l-1,l и b̂_l,l+1. Поэтому алгоритм декодирования можно выразить так: если (5.30) не выполняется для двух соседних проверочных символов, то следует изменить находящийся между ними информационный символ на противоположный.

Цепной код (5.29) позволяет исправлять ошибки, расположенные на любом месте, при условии, что между двумя любыми ошибочно принятыми имеются, по крайней мере, три правильно принятых символа. Это легко показать, исследуя алгоритмы проверки.

В последние годы широко применяют предложенные довольно давно сверточные коды, представляющие более общий класс рекуррентных кодов. Для них разработаны специальные алгоритмы так называемого последовательного декодирования, позволяющие эффективно исправлять ошибки при относительно небольшой сложности. Довольно широко используют так называемый алгоритм Витерби. Описание сверточных кодов и алгоритмов их декодирования можно найти, например в [4, 12].

Правило декодирования по наименьшему расстоянию, как отмечалось, обеспечивает максимальную верность декодирования только в симметричном канале без памяти. Для несимметричных каналов и каналов с памятью (с которыми очень часто приходится встречаться на практике) оптимальными могут оказаться другие правила. Так, в каналах с памятью вероятность возникновения ошибок кратностью q>1 зависит от того, как расположены разряды с ошибочными символами. Смежные ошибки в этих каналах могут быть более вероятны, чем ошибки, разделенные большим числом правильно принятых символов. Для таких каналов с группированием ошибок разработаны коды и методы декодирования с обнаружением или исправлением "пачек" ошибок, т. е. ошибок большой кратности, расположенных в пределах относительно небольшого числа разрядов. В частности, пачки ошибок хорошо обнаруживаются некоторыми циклическими кодами.

Для каналов с группированием ошибок часто применяют метод перемежения символов, или декорреляции ошибок. Он заключается в том, что символы, входящие в одну кодовую комбинацию, передаются не непосредственно друг за другом, а перемежаются символами других кодовых комбинаций. Если интервал между символами, входящими в одну комбинацию, сделать длиннее "памяти" (интервала корреляции) канала, то в пределах комбинации группирования ошибок не будет и можно декодировать, как в канале без памяти.

Упомянем еще один класс блочных, равномерных нелинейных кодов - коды с постоянным весом. В этих кодах все блоки имеют одинаковое число единиц. Если длина блока n, а вес w, то число М возможных блоков равно C^w_n. Так, например, при n = 7 и w = 3 М = С³₇ = 35. Все эти коды имеют d = 2, так как заменив в разрешенном блоке одну единицу нулем, а один нуль единицей, получим также разрешенный блок. Поэтому такие коды могут

гарантированно только обнаруживать одиночные ошибки. Однако их используют обычно в несимметричных каналах, в которых вероятность перехода 1→0 значительно больше вероятности перехода 0→1, или наоборот. В таких каналах очень маловероятно, чтобы в одном блоке были переходы обоих видов, и поэтому почти все ошибки приводят к изменению веса блока и, следовательно, обнаруживаются. В прежние годы эти коды широко использовали (а иногда используют и сейчас) в системах с управляющей обратной связью (см. § 5.7). Известны также более сложные коды с постоянным весом, позволяющие не только обнаруживать, но и исправлять ошибки.