5.7. Системы с обратной связью

Нередко встречаются случаи, когда информация может передаваться не только от одного корреспондента к другому, но и в обратном направлении. В таких условиях появляется возможность использовать обратный поток информации для существенного повышения верности сообщений, переданных в прямом направлении. При этом не исключено, что по обоим каналам (прямому и обратному) в основном непосредственно передаются сообщения в двух направлениях ("дуплексная связь") и только часть пропускной способности каждого из каналов используют для передачи дополнительных данных, предназначенных для повышения верности.

Возможны различные способы использования системы с обратной связью в дискретном канале. Обычно их подразделяют на два типа: системы с информационной обратной связью и системы с управляющей обратной связью. Системами с информационной обратной связью называются такие, в которых с приемного устройства на передающее поступает информация о том, в каком виде принято сообщение. На основании этой информации передающее устройство может вносить те или иные изменения в процесс передачи сообщения: например, повторить ошибочно принятые отрезки сообщения, изменить применяемый код (передав предварительно соответствующий условный сигнал и убедившись в том, что он принят) либо вообще прекратить передачу при плохом состоянии канала до его улучшения.

В системах с управляющей обратной связью приемное устройство на основании анализа принятого сигнала само принимает решение о необходимости повторения, изменения способа передачи, временного перерыва связи и передает об этом приказание передающему устройству. Возможны и смешанные методы использования обратной связи, когда в некоторых случаях решение принимается на приемном устройстве, а в других случаях на передающем устройстве на основании полученной по обратному каналу информации.

Простейшим по идее методом информационной обратной связи является метод полной обратной проверки и повторения (ОПП). При этом принятый сигнал полностью ретранслируется на передающее устройство, где каждая принятая кодовая комбинация сверяется с переданной. В случае их несовпадения передающее устройство передает сигнал для стирания неправильно принятой комбинации, а затем повторяет нужную комбинацию. В качестве сигнала для стирания применяют специальную кодовую комбинацию, не используемую при передаче сообщения.

Функциональная схема такой системы показана на рис. 5.L Передаваемое сообщение, закодированное примитивным кодом, посылают в канал и одновременно записывают в запоминающем устройстве (накопителе). Принятая кодовая комбинация сразу не декодируется, а запоминается в приемном накопителе и возвращается по обратному каналу на передающий конец, где она сравнивается с переданной комбинацией. Если они совпадают, то передается следующая кодовая комбинация, в противном случае - сигнал стирания.

При этом методе окончательный ошибочный прием кодовой комбинации возможен лишь тогда, когда ошибки в принятой комбинации компенсируются ошибками, возникающими в канале обратной связи. Другими словами, для того чтобы некоторый символ в переданной кодовой комбинации был окончательно принят ошибочно, необходимо и достаточно, чтобы, во-первых, произошла ошибка в прямом канале и, во-вторых, при ретрансляции произошла такая ошибка, которая изменит неправильный ретранслируемый символ на действительно переданный. Это позволяет сразу вычислить вероятность не обнаруженной, а следовательно, и неисправленной ошибки (в расчете на один символ):

где p₁ - вероятность ошибки в прямом канале; р₂ - вероятность противоположной ошибки в канале обратной связи.

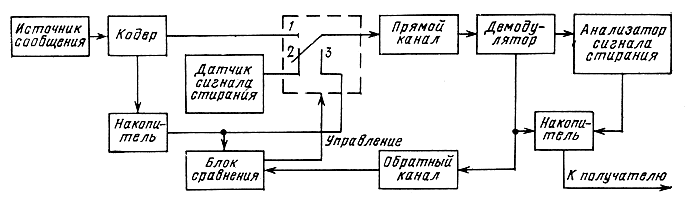
Рис. 5.1. Система с информационной обратной связью

Следовательно, если p₁ и р₂ велики, то система с полной ретрансляцией дает неудовлетворительные результаты. Практически данный метод имеет смысл в тех случаях, когда канал обратной связи обеспечивает весьма высокую верность (например, при передаче сообщений на спутник с Земли), а прямой канал имеет низкую верность (например, при передаче сообщений спутника на Землю ввиду того, что мощность передатчика на спутнике мала). Существенным недостатком системы с полной ретрансляцией является большая загрузка канала обратной связи. Существуют и более сложные системы с информационной обратной связью, в которых используются помехоустойчивые коды.

Наиболее распространены системы с управляющей обратной связью (УОС) при использовании избыточных кодов для обнаружения ошибок (рис. 5.2). Такие системы часто называют системами с переспросом, или с автоматическим запросом ошибок, или с решающей обратной связью (РОС).

В большинстве случаев это системы дуплексные, т. е. информация в них передается в обоих направлениях. В кодере передаваемое сообщение кодируется кодом, позволяющим с большой вероятностью обнаруживать возникающие в канале ошибки. Принятый кодовый блок декодируется с обнаружением ошибок. Если ошибки не обнаружены, то декодированный отрезок сообщения поступает к получателю. При обнаружении ошибок блок бракуется и по обратному каналу передается специальный "сигнал переспроса". В большинстве систем этот сигнал представляет собой специальную кодовую комбинацию, на время передачи которой прерывается поток информации, идущей по обратному каналу. Прием сигнала переспроса вызывает повторение забракованного блока, который для этого хранится в накопителе-повторителе до тех пор, пока по обратному каналу не будет принята очередная кодовая комбинация, не содержащая переспроса.

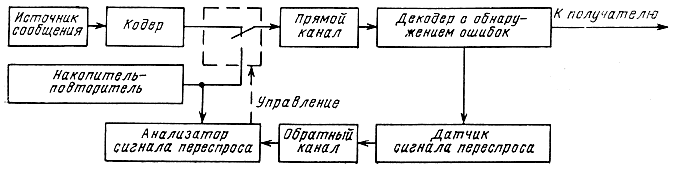
Рис. 5.2. Система с управляющей обратной связью

Система с управляющей обратной связью оказывается весьма эффективной в каналах с переменной вероятностью ошибки р (например, в каналах с замираниями). Когда величина р становится близкой к 1/2, т. е. пропускная способность канала падает почти до нуля, система находится в режиме постоянного переспроса, однако при хорошем коде ложная информация на выход практически не поступает. При уменьшении вероятности ошибки скорость передачи увеличивается, а верность продолжает оставаться на заданном уровне. Таким образом, система УОС как бы адаптируется (приспосабливается) к состоянию канала, используя канал настолько, насколько это оказывается возможным в каждом из его состояний.

В заключение отметим следующий факт, доказываемый в теории информации: в каналах без памяти наличие любой обратной связи не увеличивает пропускной способности прямого канала. Следовательно, если допустимо использование длинных кодов, то обратная связь не даст преимуществ. Однако, как уже указывалось, длинные коды требуют весьма сложных устройств декодирования, которые часто практически не реализуемы. Именно в этом случае может помочь обратная связь, позволяющая реализовать ту же пропускную способность более простыми средствами.

Вопросы к главе 5

1. По каким признакам можно классифицировать коды?
2. Источник независимых сообщений имеет в своем алфавите восемь сообщений с вероятностями Р(А) = 0,3; Р(Б) = Р(В) = 0,2; Р(Г) = 0,15; Р(Д) = 0,1; Р(Е) = 0,03; Р(Ж) = Р(И) = 0,01. Вычислите энтропию сообщений, постройте неравномерный код по методу Фено и определите, насколько он близок к оптимальному. Сравните необходимые скорости передачи в канале при коде Фено и при равномерном коде.
3. Почему короткие помехоустойчивые коды не обеспечивают большой эффективности?
4. Может ли один и тот же помехоустойчивый код использоваться в системе с обнаружением и в системе с исправлением ошибок?
5. В двоичном стирающем канале без памяти (см. гл. 3, рис. 3.7) вероятность ошибки p = 0, а вероятность стирания р_с>0. Докажите, что код с d > 1 позволяет исправлять в таком канале все стертые символы, если кратность стираний q_c<d.
6. Пусть некоторый код А длины n имеет нечетное значение d. Построим новый код В длины n+1, добавив к прежнему коду проверочный символ, равный сумме (по модулю 2) всех остальных символов. Покажите, что при этом d увеличивается на 1.
7. Покажите, что код В длины n+1, построенный в предыдущей задаче, позволяет исправлять ошибки кратностью q≤d/2-1, т. е. те же, которые исправлял код А и одновременно обнаруживать ошибки кратностью d/2, где d - четное минимальное расстояние кода В.
8. Какой код является двойственным простейшему коду (n, n-1) с одной проверкой на четность и d = 2? Чему равно d для двойственного кода?
9. При использовании кода Хэмминга (7,4) с проверочной матрицей (5.24) принята последовательность 1100111. Как она должна быть декодирована по алгоритму Хэмминга? Тот же вопрос, если принята последовательность 1100110? А если 1010001?
10. Код Хэмминга (3,1) содержит всего две комбинации: 000 и 111. Определите эквивалентную вероятность ошибки при использовании этого кода в симметричном канале с независимыми ошибками, происходящими с вероятностью р.
11. Тот же код (3,1) используется в несимметричном канале, в котором Р(1→0) = р, Р(0→1) = 0. Предложите разумное правило декодирования и вычислите эквивалентную вероятность ошибки.
12. В формуле (5.28) выписаны четыре "проверки для символа эквидистантного кода (7,3). Учитывая, что этот код циклический, запишите проверки для b₂ и b₃ и определите, как будут декодированы по мажоритарному алгоритму принятые последовательности 0100110, 0110111, 0101010?
13. Для двух кодов (6,5) и (4,3) с d = 2 у каждого, составлен итеративный код. Найдите для него n, k и d и покажите, каким образом он позволяет "справлять и обнаруживать ошибки?
14. * В двоичной системе с информационной обратной связью (ОПП) ошибки независимы и их вероятность в прямом канале pi = 0,l, а в обратном канале р₂ = 10^-5. Используются 5-разрядные кодовые комбинации. Определите вероятность не обнаруженной ошибки и оцените степень замедления передачи за счет обнаруженных ошибок.
15. * В условиях вопроса 13 p₁ = 0,5 (т. е. связь по прямому каналу отсутствует), а p₂ = 0. Возможна ли передача информации в этом случае? По формуле (5.33) вероятность не обнаруженной ошибки р_н.о = 0. С другой стороны, интуиция подсказывает, что передача информации здесь невозможна. Как объяснить такое противоречие?