
Глава 6. Прием дискретных сообщении
6.1. Прием сигналов как статистическая задача
В данной главе основное внимание уделено модему или так называемому устройству преобразования сигналов (УПС), в частности демодулятору. На его вход (см. рис. 1.5) поступает сигнал z(t) = s(t, bi) + n(i), где s(t, bi) - сигнал, соответствующий символу bi; n(t) - аддитивная помеха*. На выходе демодулятора возникает дискретный сигнал, т. е. последовательность кодовых символов. Обычно некоторый отрезок (элемент) непрерывного сигнала преобразуется модемом в один кодовый символ (поэлементный прием). Если бы этот кодовый символ всегда совпадал с передаваемым (поступившим на вход модулятора), то связь была бы безошибочной. Но, как известно, помехи приводят к невозможности с абсолютной достоверностью восстановить по принятому сигналу переданный кодовый символ.
* (Обычно в приемных устройствах демодулятору предшествуют усилители и преобразователи частоты. В данной главе все они считаются включенными в состав канала. В ряде случаев именно они являются основными источниками аддитивных помех канала.)
Каждый демодулятор описывается законом, по которому поступивший на его вход непрерывный сигнал превращается в кодовый символ. Этот закон называется правилом решения, а реализующая его схема - решающей. Демодуляторы с различными правилами решения будут выдавать, вообще говоря, различные решения, из которых одни верные, а другие - ошибочные.
В любом демодуляторе дискретных сообщений перед непосредственным принятием решения приходящий сигнал подвергается той или иной обработке, целью которой является наилучшее использование различия между реализациями сигналов, соответствующих разным символам, а также отличия сигналов от помех. Всякая линейная обработка сигнала описывается операцией интегрирования с весом φ(t, τ) в течение тактового интервала (О, Т):
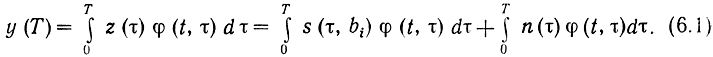
Таким образом, на выходе устройства обработки существуют сигнальная и шумовая составляющие.
В простейшем случае φ(t, τ) = δ(τ-t0), 0<t0<T, тогда y(Т) = z(t0) и обработка сводится к взятию одного отсчета приходящего сигнала в момент t0. Очевидно, что при этом не используется энергия сигнала и содержащаяся в нем информация на протяжении всей остальной части тактового интервала.
При весовой функции
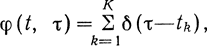
0<tk<T,
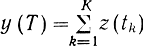
Если моменты времени tk надлежащим образом согласовать с формой сигнала, то можно накопить энергию в К отсчетах и лучше использовать информацию, содержащуюся в сигнале. Для случая, когда сигнал s(t, bi) = ai, т. е. остается постоянным на протяжении тактового интервала, выбор φ(t, τ) = 1 дает
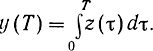
Это случай интегрального приема - предел накопления при K→∞.
Очень часто линейная обработка сигнала осуществляется с помощью фильтров. В этом случае φ(t, τ) = g(t-τ) - импульсная реакция фильтра.
Помимо операции (6.1) сигнал нередко подвергают нелинейной обработке - детектированию, возведению в степень и т. д. На ранних этапах развития техники связи способы обработки
сигналов выбирались разработчиками аппаратуры интуитивно, исходя из общих идей о путях выделения сигнала из помехи и различения передаваемых символов. Выбором различных видов реализаций сигналов s(t, bi) и способов обработки в ряде случаев удавалось повысить помехоустойчивость системы передачи дискретных сообщений, т. е. увеличить верность оценки переданного символа bl при наличии помех.
Современная статистическая теория связи позволяет отыскать наилучшую операцию обработки входного сигнала z(t), обеспечивающую максимальное качество оценки b̂i. Будем полагать, что свойства источника сообщения и кодера известны. Кроме того, известен модулятор, т. е. задано, какая реализация элемента сигнала соответствует тому или иному кодовому символу, а также задана математическая модель непрерывного канала. Требуется определить, каков должен быть демодулятор (правило решения), чтобы обеспечить оптимальное (т. е. наилучшее из возможных при. заданных сигналах на передаче) качество приема.
Такая задача была впервые поставлена и решена (для гауссовского канала) в 1946 г. выдающимся советским ученым В. А. Котельниковым. В этой постановке качество оценивалось вероятностью правильного приема символа. Максимум этой вероятности при заданном виде модуляции В. А. Котельников назвал потенциальной помехоустойчивостью, а демодулятор, обеспечивающий этот максимум, - идеальным приемником. Из этого определения следует, что ни в одном реальном демодуляторе вероятность правильного приема символа не может быть больше, чем в идеальном приемнике.
На первый взгляд принцип оценки качества приема вероятностью правильного приема символа кажется вполне естественным и даже единственно возможным. Ниже будет показано, что это не всегда так и что существуют и другие критерии качества, применимые в тех или иных частных случаях.
Ознакомимся подробнее со статистическим подходом к задаче приема дискретных сообщений на фоне шумов. Пусть при передаче дискретных сообщений, закодированных кодом с основанием m используются реализации сигнала ui(t), 0<t<T, соответствующие кодовым символам bi (i = 0, 1, 2, 3,..., m-1)*. В течение тактового интервала** 0<t<T на вход приемного устройства поступает колебание z(t), которое вследствие искажений и помех в канале не совпадает в точности ни с одним из сигналов ui(t). Следовательно, в этом случае приемное устройство должно выбрать одну из m возможных взаимоисключающих (альтернативных) гипотез: передавался кодовый символ b0, т. е. сигнал u0(t);
передавался кодовый символ b1 т е. сигнал um-1(t).
Для двоичной системы (m = 2) приемное устройство выбирает одну из двух альтернативных гипотез о передаче символа 1 или 0.
* (Без потери общности можно в дальнейшем, когда это удобно, считать bi = i.)
** (Начало этого интервала для удобства совместим с началом координат. В принципе, интервал анализа не всегда совпадает с тактовым интервалом Т. Отрезок сигнала на тактовом интервале называют элементом сигнала.)
Совокупность всех возможных реализаций z(t) можно интерпретировать точками в пространстве Z принимаемых финитных сигналов. Обычно оно является бесконечномерным пространством Гильберта или, с некоторыми (приемлемыми для практики) оговорками, многомерным пространством Евклида. Простоты ради будем графически изображать реализации принимаемых сигналов si(t) и помехи n(t) длительностью Т точками на плоскости (рис. 6.1) или соответствующими векторами, откладываемыми от начала координат 0. Если правило решения выбрано, то это означает, что каждой точке пространства принимаемых колебаний (концу вектора) z = s + n приписывается одна из m гипотез, т. е. определенный передаваемый кодовый символ bi. Пространство принимаемых сигналов окажется при этом разбитым на m не пересекающихся областей Bi, каждая из которых соответствует принятию определенной гипотезы. В такой трактовке различные приемные устройства отличаются друг от друга способом разбиения пространства сигналов на области Вi т. е. правилом принятия решения*. Возможное разбиение схематически показано на рис. 6.1.
* (В математической теории связи это разбиение и называют решающей схемой. Заметим, что в некоторых случаях пользуются решающей схемой со стиранием, или отказом от решения. Это значит, что m областей не охватывают всего пространства сигналов z, и если приходящий сигнал не попадает ни в одну из этих областей, то принимается решение о стирании либо о невозможности определить передаваемый символ.)
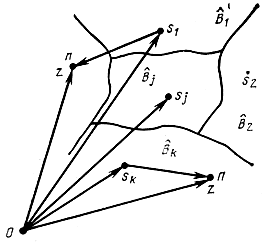
Рис. 6.1. Разбиения пространства принимаемых колебаний на непересекающиеся области
В двоичной системе пространство z разбивают на две не пересекающиеся области В̂0 и B̂1. Пусть на интервале 0-T принимается колебание
Z(t) = sj(t) + n(t), (6.2)
где sj(t)-полезный сигнал в месте приема, прошедший канал связи, а n(t) - реализация аддитивной помехи.
Если помехи отсутствуют, возможные значения z(t) изображаются точками sj (j = 0, 1, 2, ..., m-1). При наличии помехи и передаче сигнала с номером j точка принимаемого колебания z отклоняется от точки sj.
На рис. 6.1 это показано для сигналов S1 и Sk. Обычно область В̂j, содержит точку sj. В тех случаях, когда помеха не выводит точку z за пределы области B̂j решение оказывается верным.
В противном случае возникает ошибка. Очевидно, изменяя границы между областями, можно влиять на вероятность ошибочного приема отдельных передаваемых символов. Например, если в разбиении, показанном на рис. 6.1, расширить область B̂j за счет области B̂k, то уменьшится вероятность ошибочного приема символа bk вместо передаваемого символа bj. Однако в этом случае возрастает вероятность ошибочного приема b̂j при передаваемом bk. Очевидно, всегда существует такое расположение областей, которое в определенном смысле лучше всякого другого.
Если задан критерий качества, то наилучшее разбиение пространства принимаемых сигналов (оптимальная решающая схема приемного устройства) достигается методами теории статистических решений.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
